The many incomprehensible properties of the world are associated with the nature of mass and energy (as well as impulse). We all heard these words and many of us have a vague idea of their meaning. Of course, the meanings of the words "mass" and "energy" in English and other languages are quite a lot. Unfortunately, none of them coincides with those that are meant by physicists. Try to put aside these meanings of words and work with exact physical concepts - otherwise you will be completely confused.
It should be noted that when it comes to the phrase “mass and energy,” it is not worth remembering another popular couple, “substance and energy.” Many people mention the last phrase as if substance and energy are two sides of the same coin. But it is not. Substance and energy belong to different categories, like apples and orangutans. A substance, no matter how to define it, is a class of objects existing in the Universe, and mass and energy are not objects, but properties which these objects possess. Mass and energy are deeply intertwined with each other, and deserve a general explanation.
To understand mass and energy, it is necessary to add momentum to them and discuss the differences and relationships of these quantities.
Energy
The word "energy" has many meanings. When we get sick, we are talking about the fact that we have no energy left, having in mind strength and motivation. When we say that someone is full of energy, we mean his high activity. We complain about rising energy prices, keeping in mind the fuel. We speak of spiritual energy as something immeasurable, but important, perhaps some form of charisma. And all these concepts are in common with each other, so we choose one word to describe them. But in physics, energy is another. From the point of view of physics, it will be mistaken to mix one of these definitions with the physical one. In physics, you need to adhere to the physical term, so as not to get the wrong answers and not get completely confused.
Unfortunately, the concept of "energy" in physics is very difficult to describe as dictionaries do with a short meaningful phrase. But do not think bad - the whole thing is in the imperfection of the natural language, and not in the fact that the concept of energy in physics is vague. In any given physical system, it is completely clear what its energy is, both in the sense of its experimental measurement, and in the sense of calculations (in the presence of describing the system of equations).
One of the reasons why energy is so difficult to describe is because it can take many forms, and not all of them are easy to understand. Here are the three most common varieties:
1. Energy can be enclosed in the mass of an object. Here I call this option “mass energy” (due to the well-known equation E = mc
2, energy is associated with mass. It is also called “rest energy” because it is the energy of an object that is at rest, that is, without movement).
2. Secondly, energy is associated with the movement of an object. Here I call it “the energy of motion”, and the technical term for this is kinetic energy. This option is intuitively easy to perceive, since the fast moving objects have more energy than the slow moving ones. In addition, a heavy object has more moving energy than a light one moving at the same speed.
3. Energy can be stored in the relationship of objects (and is usually referred to as “potential”). It is stored in a stretched spring, in water behind a dam, in the gravitational interaction of the Earth and the Sun, in interactions of atoms in a molecule. There are many ways to store energy. It sounds vague, but the language is to blame. In any of the cases listed above, there are exact formulas describing the energy stored in the system and well-defined ways to measure it.
The third type of energy is associated with what I will call the interaction energy, and this is the most complicated concept of all. In contrast to the energy of mass and the energy of motion, which are always greater than or equal to zero, the energy of interactions can be positive and negative. For the time being I will leave this topic, but we will come back to it.
Energy is a special magnitude of great importance for physics. The reason for this importance is that it is “preserved”. What does this mean?
If you start observation from an object or from a set of objects - let's call them “system of objects” - possessing a certain amount of energy at the initial moment (do not forget to count all the energy - masses, movements, stored energy of all types, etc.), and then parts of the system will interact only with each other and nothing else, then at the end of the observation the total amount of energy these objects possess will be the same as at the beginning. The total energy of the system is saved - its total number does not change. It can change shape, but if you track all the varieties, then at the end it will be as much as at the beginning.
This rule works even if some objects disappear and give way to others, for example, if
one particle in the system falls into two others , flowing into the system.
Why is energy conserved? Because of the mathematical principle that relates the fact that the laws of nature do not change with time, with the existence of a conserved quantity, which we call “energy” by definition.
We owe the most famous and general definition of this principle to
Emmy Noether , one of the greatest mathematical physicists of the previous century, Einstein's contemporaries. Some members of the physical and mathematical community treated her
with deep respect , but at that time in her native Germany she suffered from discrimination based on gender and ethnicity (they blocked attempts to assign her the title of professor in
Göttingen , and from there she had to flee after came to power the Nazis). After emigrating to the United States, after only two years of teaching at
Bryn-Mar College (which still accepts only women to study), she died from cancer.
The famous
Noether theorem (actually these are two closely related theorems) tells us that if there is symmetry in the laws of nature - in our case, this means that the laws of nature are the same at any time - then it follows that some value is preserved - in our case, energy .
Moreover, the theorem exactly tells us what this quantity is - what are the various forms of energy for a given system of objects that need to be added up in order to obtain the total energy. That is why physicists always know exactly what energy is, and why it is easier to get it using equations than to define with words.
Pulse
With impulse, the situation is approximately the same as with energy. The laws of nature are the same everywhere. Roughly speaking, experiments give the same answers, whether you spend them north or south of here, west or east, on top of a building or in a deep mine. Choose any direction in space. Then, according to Noether, the momentum along this direction is preserved. Since there are three dimensions in space, one can move in three different independent directions and there are three independent conservation laws. You can choose any three directions, provided that they are different. For example, you can choose impulses in the directions of north-south, west-east and up-down as the three laws of conservation. Or you can choose three others - towards and from the Sun, along the Earth's orbit in both directions, and up and down relative to the plane of the Solar System. Your choice does not matter, for the momentum is maintained along any direction.
The simplest form of impulse arises due to the simple movement of objects, and this is approximately what one can imagine intuitively: if an object moves in a certain direction, then it has an impulse in that direction, and the faster it moves, the greater this impulse. A heavier object has a larger impulse than a light one, if they move with the same speeds.
One of the interesting consequences of this conservation is: if you have a fixed system of objects (that is, the system as a whole does not move, if you average all the movements of its constituent objects), then it will remain stationary unless it is given by any external movement. impact. The reason is that in a fixed system, the total impulse is zero, and since the impulse is preserved, it will remain zero forever, unless something outside the system intervenes.
Mass, and its connection with energy and momentum
Now turn to mass
Unfortunately, there is a lot of confusion with mass - after the release of Einstein’s work on the theory of relativity, for a while there were two concepts of mass. And only one of them (the one on which Einstein himself stopped, and which is sometimes called the "invariant mass" or "rest mass" to distinguish it from the already archaic term "relativistic mass", is still used in particle physics. In a separate article, I will explain this in more detail.
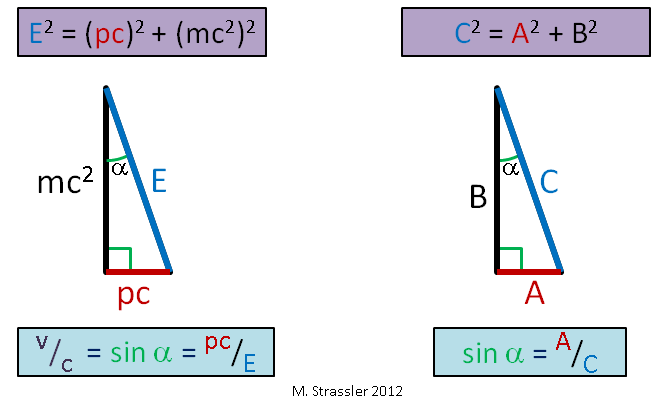 Fig. one
Fig. oneUnder the mass m, which I use in the articles, is meant the mass that directly connects energy and momentum. For an object moving without the influence of external forces (not interacting significantly with other objects), Einstein suggested (and this was confirmed by experiments) that its energy E, momentum p and mass m satisfy simple Pythagorean equality:
E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (equation # 1)
E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (equation # 1)
Remember the old man Pythagoras, who claimed that for a right triangle with sides A and B and hypotenuse C, the equality
C 2 = A 2 + B 2 ? This is a connection of the same type - see fig. 1. We have a constant speed, which, as we shall see, serves as a universal speed limit. We will also see why it is called the "speed of light."
According to Einstein's equations, the speed of an object divided by the speed limit c is simply the ratio of pc to E:
v / c = (p c) / E \ qquad (equation # 2)
v / c = (p c) / E \ qquad (equation # 2)
That is, the ratio of the horizontal leg to the hypotenuse. It is also equal to the sine of the angle α in fig. 1. So here, citizens. And since the legs of a right-angled triangle are always shorter than the hypotenuse (the sine of any angle is always less than or equal to 1), the speed of any object cannot exceed c, the universal speed limit. With an increase in the velocity of an object of a fixed mass, p and E become very large (Fig. 2), but E is always greater than pc, therefore v is always smaller than c!
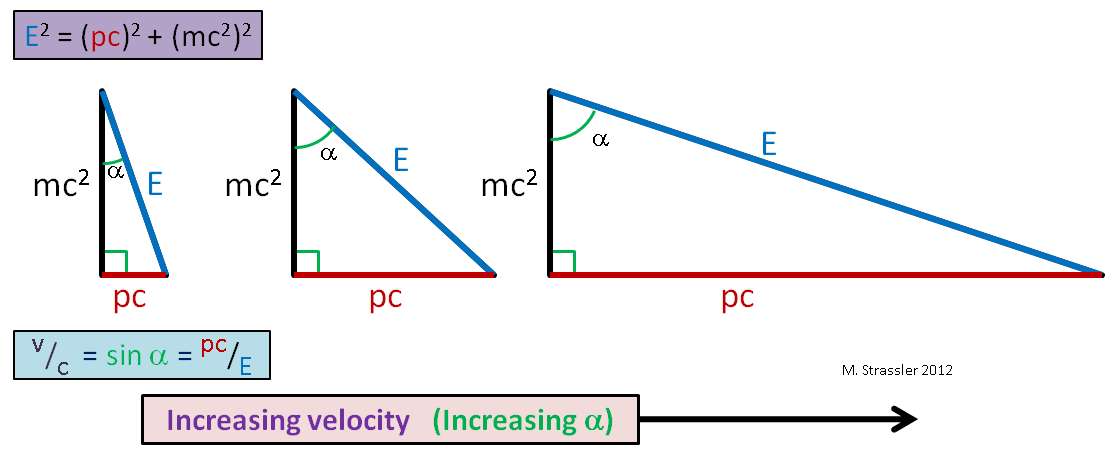 Fig. 2
Fig. 2Now note that if an object does not move, then its momentum p is zero, and the ratio in equation 1 reduces to:
E 2 = ( m c 2 ) 2 , q u a d o r q u a d E = m c 2
Einstein's famous formula, the connection of mass with a fixed amount of energy (what I call mass energy), is simply a statement corresponding to the fact that when a triangle degenerates into a vertical line, as in fig. 3 on the left, his hypotenuse becomes the same length as the vertical leg. However, it does not mean that the energy is always equal to the mass multiplied by the square of c. This only works for a resting object with zero momentum.
 Fig. 3
Fig. 3Another interesting observation: for a massless particle, the vertical leg of the triangle is zero, and the hypotenuse and the horizontal leg coincide, as in fig. 3. In this case, E equals pc, which means that v / c = 1, or v = c. It is seen that a massless particle (for example, a photon, a particle of light) inevitably moves with speed c. Therefore, the speed of light is the same as the universal speed limit, c.
On the other hand, if we take a particle possessing a mass, as in Fig. 4, it doesn’t matter how big you make the momentum and energy, E will always be a little more than p * c, so the speed will always be less than c. Massless particles must travel at maximum speed. The speed of massive particles should be less.
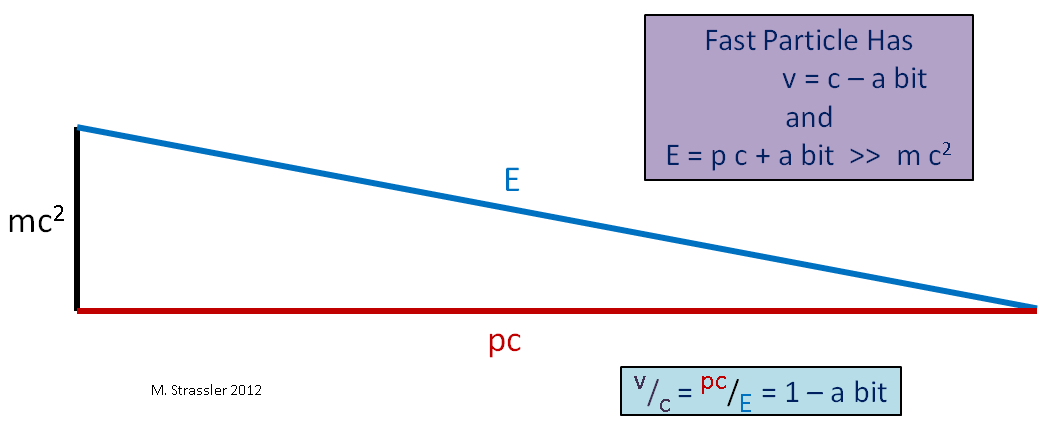 Fig. 4. Here ">>" means "much more."
Fig. 4. Here ">>" means "much more."Imagine another borderline case, slowly (compared to the speed of light) moving a massive object, for example, a car. Since its velocity v is much less than c, its momentum p multiplied by c will be much less than E, and, as can be seen from fig. 5, E will be slightly more than mc
2 . Therefore, the energy of motion of a slow object E - mc
2 is much less than the energy of its mass mc
2 , and for a fast object the energy of motion can be made arbitrarily large, as we saw in Fig. four.
One subtle point: the impulse is not only a number, but also a vector. He has size and direction. It is directed towards the particle motion. When I write "p", I only specify the value. In many cases, it is necessary to track the direction of the pulse, although this is not necessary in equation 1, which relates the pulse to energy and mass.
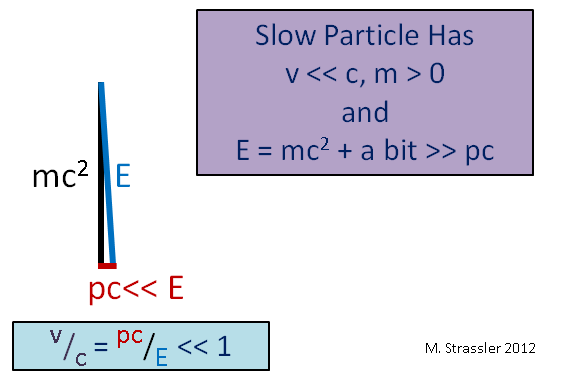 Fig. five
Fig. fiveAnother subtle point: I used triangles and simple trigonometry, since it is known to everyone from school. Experts, on the other hand, need to be careful - you can correctly understand Einstein's equations using
hyperbolic functions , which are usually not found for amateurs, but extremely important for understanding the structure of the theory, and making things more understandable, such as adding speeds, compressing distances, etc. Non-applicants can ignore this.
But is speed relative? ..
If you carefully read the text, you may already be surprised at something. You know that the speed of a particle - or anything that moves more slowly than light - depends on the point of view.
If you sit at home and read a book, you will say that the speed of the book is zero (and it really rests relative to you), therefore, it has no impulse and energy of movement, only the energy of the mass. But if I stood on the Moon, I would remind you that the Earth is spinning, so this rotation enthralls you and moves you relative to me at a speed of hundreds of kilometers per hour. So you and your book would have an impulse from my point of view.
Who is right?
The variant of relativity according to Galileo - the first principle of relativity - states that both of us are right. Einstein’s version of relativity agrees with Galileo’s point of view that both are right, but makes important adjustments to how Galileo’s followers would have identified the energy, momentum and mass of the book, putting these values in the Pythagorean equation of №1.
But if everything is right, what E and what p I need to substitute into the energy / momentum / mass ratio,
E 2 = ( p c ) 2 + ( m c 2 ) 2 ? Substitute E and p, measured by you reading the book, that is, E = mc
2 and p = 0? Or substitute E and p, which the book possesses from my point of view, when you move together with the Earth?
The answer to this question contains the whole essence of Einstein's No. 1 equation. Each observer will measure different values of E and p for the book, depending on how quickly the book will move relative to it. But for all observers, the equation
E 2 = ( p c ) 2 + ( m c 2 ) 2 will be true!
Magic! And in fact, genius is a thought that came in 1905 about how to replace the set of equations proposed by Newton and his followers with a new amazing set of equations that still coincides with all previous experiments, but it turned out to be a more accurate representation of reality. It’s hard to imagine how much you had to change your way of thinking, to think of it, until you figure out how much everything could have gone wrong during the formation of the theory, and how many other different equations containing contradictions with mathematics or with previous experiments can it would offer (and people offered them). For example, I constantly receive the work of novice physicists trying to “correct” the Einstein equations, but I have never seen any of them check their equations for internal consistency. This is a very difficult task and the reason for the failure of most theories.
But how then can energy and momentum be conserved?
Wait a minute - you will say when your head is ready to explode and splash everything around with brains (I myself remember this feeling) - but the energy and impulse must be preserved! So how can different observers disagree with what they are?
There is even more magic, which, by the way, was even before Einstein. Believe me, the Universe is a very, very clever accountant, and, despite the fact that different observers will not agree on the energy available to an object or a system of objects, they will all agree that this energy does not change with time. The same goes for impulse.
But the mass is very different from energy and momentum. First, the mass is not saved. In nature, there are many processes that alter the total mass of the system: for example, a massive Higgs particle can decay into two massless photons. Symmetry is not connected with the mass, and therefore Noether does not have a conservation law for us. Secondly, unlike energy and momentum, whose magnitudes depend on the observer (in particular, on his speed in relation to the measured objects), all observers will agree with the mass m of the object. And this is not at all obvious, and it happens so because the Einstein equations work awfully cleverly.
So what we have
At the moment we have some seemingly contradictory knowledge. We know that:
• The energy and impulse of an isolated physical system is conserved (the total energy and the total impulse of an isolated system do not change with time) from the point of view of any observer.
• Different observers moving relative to each other, differently estimate the magnitude of the energy and momentum of the system!
• The sum of the masses of the objects that make up the system is not preserved; it may change.
• But all observers will agree with the magnitude of the mass of the object.
Two more facts and two conclusions should be added to this list:
The mass of the physical system of objects is not equal to the sum of the masses of the objects that make up this system.
Instead, the mass of the physical system, about which all observers agree, is determined by its energy and momentum, and satisfies its version of equation No. 1:
(E_ {system}) ^ 2 = (p_ {system} c) ^ 2 + (m_ {system} c ^ 2) ^ 2 \ qquad (equation # 1 ')
It turns out that the additional conservation law is not needed, and that although the sum of the masses of the objects that make up the system is not conserved, the mass of the system is preserved, since it is connected via equation No. 1 with the energy and momentum of the system, which are conserved.
The mass of the object system is the only item on our list that is both persistent and not the subject of dispute by observers.It is only necessary to remember that the mass of the system of objects is not the sum of the masses of the objects that make up the system, but that which is given by equation 1.
Than trying to explain it, just see how it works. A vivid example is worth a thousand words.
Let us consider the most fashionable thing as an example of a system, namely, the Higgs particle (having a mass of 126 GeV / s 2 ), and see how the various statements made above work when it decays into two photons.One Higgs particle, two photons and three observers
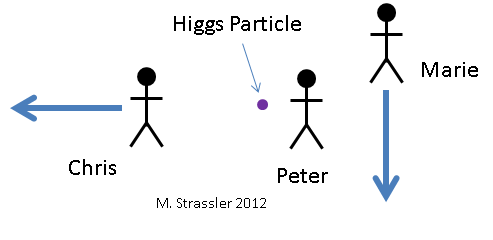 Fig. 6. Three observers look at the Higgs particle. In relation to her, Peter (Peter) does not move, Masha (Marie) moves down, and Kostya (Chris) moves to the left.Let's look at how the Higgs particle splits into two photons from the point of view of three different observers. They are shown in Fig. 6 with the Higgs particle they are looking at. Of course, they cannot see through her eyes, for she exists too small a time interval and she is too small. They need to use any scientific equipment. For Petit, the Higgs particle does not move. Masha moves down relative to Petit. Kostya moves left relative to Petit. So, for Masha, the Higgs particle moves up, and for Bones, it moves to the right. Three observers see the particle decay according to fig. 7. Peter sees that Higgs splits into two photons of the same energy, one of which moves up, and the other moves down. Masha sees that Higgs splits into two photons of different energies, and the energy moving upwards is greater than that of the movement downwards.Kostya sees how Higgs splits into two photons, going right up and right down. Let's calculate what energy and pulses the observers will assign to Higgs and two photons, and how each of them will come to the conclusion that energy and momentum are conserved during the decay process.
Fig. 6. Three observers look at the Higgs particle. In relation to her, Peter (Peter) does not move, Masha (Marie) moves down, and Kostya (Chris) moves to the left.Let's look at how the Higgs particle splits into two photons from the point of view of three different observers. They are shown in Fig. 6 with the Higgs particle they are looking at. Of course, they cannot see through her eyes, for she exists too small a time interval and she is too small. They need to use any scientific equipment. For Petit, the Higgs particle does not move. Masha moves down relative to Petit. Kostya moves left relative to Petit. So, for Masha, the Higgs particle moves up, and for Bones, it moves to the right. Three observers see the particle decay according to fig. 7. Peter sees that Higgs splits into two photons of the same energy, one of which moves up, and the other moves down. Masha sees that Higgs splits into two photons of different energies, and the energy moving upwards is greater than that of the movement downwards.Kostya sees how Higgs splits into two photons, going right up and right down. Let's calculate what energy and pulses the observers will assign to Higgs and two photons, and how each of them will come to the conclusion that energy and momentum are conserved during the decay process.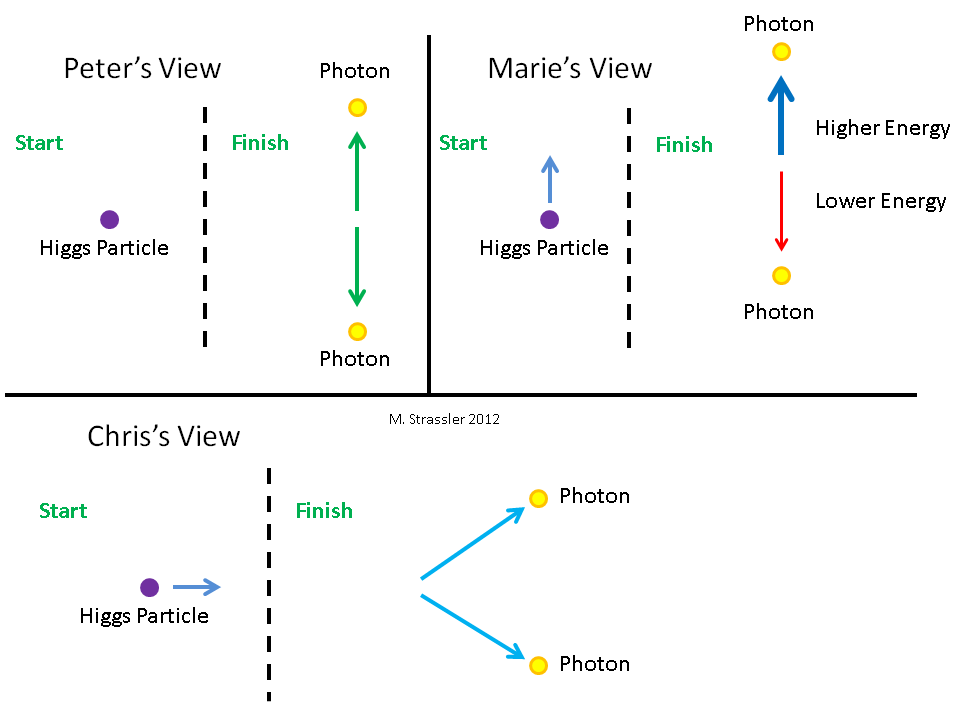
Decay of the fixed Higgs particle
To begin with, let's look at the Higgs particle from Petit's point of view. Petya looks (with the help of measuring instruments) at the Higgs particle, and what does he see? (I will put a line over everything that Petya sees, and then we will compare it with the observations of Masha and Bones). Higgs does not move, so his impulse¯ p 0 is zero, and according to equation # 1 it has, with its mass m = 126 GeV / c2, theenergy will be¯ E 0 =mc2=126GeBNow, according to the conservation of energy and momentum, the system consisting of the Higgs particle will save all energy and momentum after the decay. And this will be so until no external force affects the Higgs. You may ask if we need to worry about gravity, because gravity will be an external influence that can change the momentum. My answer is that in the short time that Higgs needs for decay, the effect of gravity will be so small that if I told you what it really is small, you would giggle. Forget about it.So, when the Higgs decays, the energies of the particles that make up its remnants should give a total of 126 GeV, and the impulse of the particles (given that the impulse is not only a magnitude, but also a direction - a vector) gives a total of zero.Two massless photons that Higgs splits into can scatter in all directions, but to simplify the example, imagine that they will scatter vertically — one up, and the other, bouncing off, down. (We will discuss a little later why they should scatter in opposite directions).What is the momentum of photons? It's simple. First, the total impulse of the system — the sum of the impulses of two photons — must be zero, since the Higgs had zero momentum before the decay (from Petit's point of view). Now each of the photons has a pulse of a certain size and direction. In sum, they can only give zero in one way - if they are of equal size and the opposite direction. If one goes up, the other must go down, and their magnitude should be the same. Fig. 8: what Peter sees. Secondly, the total energy of the system is the sum of the energies of two photons. This is because there is no interaction energy between them (except for extremely small gravitational attraction, which can be forgotten). Of course, since they have no masses, then all their energy is in the energy of motion. In addition, in the case of a massless particle, equation 1 indicates that E = pc, where p is the momentum value. Because of this, two photons with the same pulses must have the same energies. And since the two of these energies in sum must give the energy of the Higgs particle, the energy of each photon must be equal to half the energy of the Higgs particle.
Fig. 8: what Peter sees. Secondly, the total energy of the system is the sum of the energies of two photons. This is because there is no interaction energy between them (except for extremely small gravitational attraction, which can be forgotten). Of course, since they have no masses, then all their energy is in the energy of motion. In addition, in the case of a massless particle, equation 1 indicates that E = pc, where p is the momentum value. Because of this, two photons with the same pulses must have the same energies. And since the two of these energies in sum must give the energy of the Higgs particle, the energy of each photon must be equal to half the energy of the Higgs particle.¯ E 1= ¯ E 2=1/2(126FeB)=63TeB
And since for a massless particle p = E / c, then¯ p 1=63GeB/c↑¯ p 2=63GeB/c↓
And this is shown in Fig. eight.
Energy and momentum are conserved, but mass is not, since photons have no mass, but Higgs had it. What about the mass of the system? What is the mass of a two-photon system? Nonzero. Obviously what she is. In the same way as for Higgs himself (of which the whole system was originally composed), a system of two photons has the same energy and impulse that Higgs had:E s y s t e m = ¯ E 1 + ¯ E 2 = 63 + 63 = 126 p s y s t e m = ¯ p 1 ↑ + ¯ p 2 ↓ = 63 T e B / c ↑ + 63 T e B / c ↓ = 0
And since for Petit p s y s t e m = 0 ,
m s y s t e m = E s y s t e m / c 2 = 126 G e B / c 2
That is the Higgs mass. The mass of the system has not changed during the collapse, as expected.The watcher for whom the Higgs moves up
Masha moves down in relation to Pete, so from her point of view Petya and Higgs move upwards. Assume that the Higgs moves at a speed of v = 0.8 c, that is, 4/5 of the speed of light relative to it. Unlike Petit, from the point of view of Masha Higgs has a non-zero pulse, and the pulses of photons turn out to be different in size, but still multidirectional - as a result, the sum of their pulses will be non-zero. Fig. 9: how Masha sees the decay of the Higgs particle.How to calculate the momentum and energy that a Higgs and two photons possess into which it decays, from the point of view of Masha? For this we need another set of simple Einstein equations. Suppose, from the point of view of some observer, an object has a momentum p and energy E. Then, from the point of view of another observer moving at speed v in the direction of movement of the object (or against it), the momentum and energy of the object will be expressed as:
Fig. 9: how Masha sees the decay of the Higgs particle.How to calculate the momentum and energy that a Higgs and two photons possess into which it decays, from the point of view of Masha? For this we need another set of simple Einstein equations. Suppose, from the point of view of some observer, an object has a momentum p and energy E. Then, from the point of view of another observer moving at speed v in the direction of movement of the object (or against it), the momentum and energy of the object will be expressed as:p = γ ( ¯ p + v ¯ E / c 2 )( Y p and a n e n and e № 3 )E = γ ( ¯ E + v ¯ p )( Y p and a n e n and e № 4 )
Where γ satisfies one more Pythagorean equation:1=v2/c2+1/γ2(№5)
according to Einstein. This allows us to perform transformations between what Peter sees and what Masha sees (or any other observer moving at speed v). What we discover is shown in fig. 9.
In order to compare Masha's observations with those of Petit, we need v and γ. I argue that if v = 4/5 c, then γ = 5/3.Check using equation number 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25Petya says that Higgsp0=0,E0=126 .
What about Masha? She says that:p0=γv¯E0=(5/3)(4/5)¯E0=168/c↑E0=γ¯E0=(5/3)¯E0=210
Peter claims that two photons ¯E1=¯E2=63, and for each of them E = p c. Now we can calculate what Masha sees using equations # 4 and # 4.E1=γ(1+v)¯E1=189,p1=E1/c↑
E2=γ(1−v)¯E2=21,p2=E2/c↓
Works! Energy is conserved from the point of view of Mary, forE0=210E1+E2=(189+21)=210
The impulse is also saved:p0=168/c↑p1+p2=189/c↑+21/c↓=(189–21)/c↑=168/c↑
The mass of the system coincides with the Higgs mass before and after the decay, because before and after the decayEsystem=210psystem=168/c↑
Which, according to equation # 1 ', brings the mass of the system back to 126/c2 , like Petit, because2102=1682+1262
The observer, in terms of which the Higgs moves to the right
What do we have with Kostya? Kostya moves left relative to Petit, for example, at a speed of v = 4/5 c, so relative to Kostya Higgs (and Peter) move to the right with a speed v = 4/5 c. The same calculations that we did for Masha show that the Higgs energyE0=210p0=168, but, unlike Masha, for whom the Higgs moves up, for Bones, the Higgs impulse is directed to the right. This is shown in fig. ten.
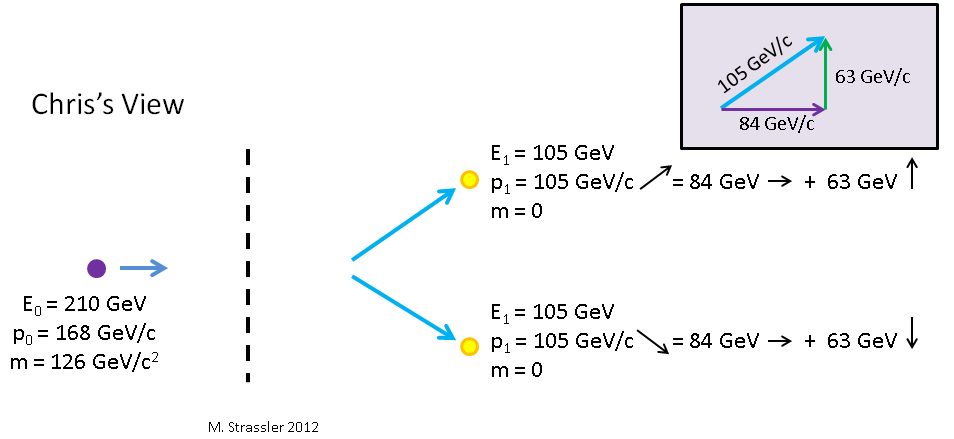
Fig. ten
Higgs splits into two photons. If, from Pett’s point of view, photons move up and down, then for Kostya, who is observing how Higgs and Peter are moving to the right, one of the photons moves to the right upwards, and the other - to the right downwards. What kind of impulse and energy will they have then?Through equations 4 and 5, we are not aware of this, since they are intended for cases where the particle and the observer move in the same direction. For our case, the equations are as follows:↕p=↕¯p↔p=γ([↔¯p]+v¯E/c2)E=γ(¯E+v[↔¯p])
These equations will be simpler than they seem, because from the point of view of Petit, p has no component moving from left to right, and the whole impulse goes up or down. So Kostya observes the following values for Higgs:↕p0=↕¯p0=0↔p0=γv¯E0/c2=(5/3)(4/5)126/c=168/c→E=γ¯E0=(5/3)126=210
And the photon going up↕p0=↕¯p1=63/c↑↔p0=γv¯E1=(5/3)(4/5)63/c=84/c→E=γ¯E0=(5/3)63=105
For the second photon, the formulas are the same, only its vertical component is directed downwards. Notice that for both photons E = pc, according to the Pythagorean theorem, for the size p of each of the pulses - according to the inset in Fig. ten
p21=(↑p1)2+(→p1)2(105/c)2=(63/c)2+(84/c)2
And again, Kostya observes other values of energy and momentum, compared with Petya and Masha. But for Kostya, energy and momentum are still saved. Kostya also observes that in a system with two photons the mass coincides with the Higgs mass. Why?
The total vertical part of the pulse system is zero, it is mutually destroyed. The horizontal part of the system pulse is 168 GeV / s. The total energy of the system is 210 GeV. This is the same as Masha observed, except for the fact that her system impulse went up, not to the right. But the direction of the pulse does not affect equation number 1 '. Only its size plays a role. So, like Masha, Kostya sees that the mass of a system of two protons is obtained126/c2 equal to the mass of the primary Higgs particle.Total
So we see that there are three different observers. Their observations:• differ in terms of the Higgs energy and momentum,• differ in terms of the energy and momentum of both photons,• agree on the conservation of energy and momentum during decay,• therefore, they agree that the mass of the system is preserved,• agree that the mass of the system is 126 GeV / c 2 ,• and moreover, that the sum of the masses of the objects of the system is not preserved, but decreases from 126 GeV / c 2 to zero.And this is not by chance. Einstein from previous experiments knew that energy and momentum are conserved, so he searched and found equations that preserve this feature of the world. Also in the process, he found that the mass of the system must satisfy equation number 1 '.Bonus: how it is used in the search for the Higgs particle
Scientists:• observe proton collisions, resulting in the birth of two photons;• calculate the mass of a system of two photons (in technical jargon this is called the invariant mass of a pair of photons).When an experiment results in a Higgs particle, which decays into two photons, then regardless of the direction and speed with which the particle moves relative to the laboratory, a system of two photons into which it will decay will always have a mass equal to the Higgs particles that produced them! Therefore, unlike random processes, which result in a system of two photons of random mass, Higgs particles will always generate a system of two photons of the same mass. Therefore, if the results of the experiment appear Higgs particles, and if they sometimes decay into two photons, we will see a peak from the Higgs decays, towering above the smooth background of other random processes. So it happened in the experiment on the LHC!