In my
article on energy and mass and related concepts, I focused on the particles — field perturbations — and the equations with which Einstein linked their energy, momentum, and mass. But energy also arises in other places, not only due to particles. To truly understand the Universe and how it works, it is necessary to understand that energy can come from the interaction of various fields, or even from the interaction with the field itself. The entire structure of our world - protons, atoms, molecules, bodies, mountains, planets, stars, galaxies - is the result of the presence of this type of energy. In fact, many types of energy, which we argue about as if they differ from each other — chemical energy, nuclear energy, electromagnetic energy — are either a form of interaction energy or in some way belong to it.
When students begin to teach physics, this type of energy includes what teachers call "potential energy." But since the word “potential” in English [and Russian] means not the same as in physics, and since the way this concept is presented is very different from the modern physical point of view, I prefer to use a different name for this energy - so that it does not communicate with the reader's ideas, right or wrong.
In addition, in the article about mass and energy, I called the interaction energy "energy of relationships". Below it will be clear why - but I decided that it was a bad idea and switched to another naming.
Preamble: concept revision
From the current point of view, preferred by physicists and tested in experiments, the whole world consists of fields. The most intuitive example of a field is the wind:
• It can be measured everywhere
• It can be zero or nonzero,
• It can pass waves (which we call sound).
In most fields, waves can form, and due to quantum mechanics, these waves cannot be of as high an arbitrarily small height.
The wave of the smallest possible height — or the smallest amplitude and the smallest power — is called a “quantum” or, often, a “particle” - however, the latter option sometimes leads to confusion.
A photon is a quantum, or a particle of light (by “light” it means both the visible part of the spectrum and other variations). This is the dimmest possible flash of light, the least powerful wave in an electric and magnetic field that can be created. You can create two photons, three or sixty-two. You can not create a third photon or two and a half. Your eyes are designed to absorb one photon at a time.
The same applies to electrons, muons, quarks, W particles, the Higgs particle, and all the rest. All these are quanta of their fields.
At the same time, the quantum, although it will be a disturbance of the field, behaves like a particle:
• Keeps integrity when moving in empty space.
• Possesses certain, albeit dependent on the observer, energy and momentum.
• Possesses a certain mass, independent of the observer.
• May be radiated or absorbed as a unit.
Let me remind you that in particle physics, mass is commonly understood as what was formerly called the “rest mass”, for which the equation E = mc 2 is satisfied only if the particle is at rest. In a moving particle, E> mc 2 , since the energy of its mass is equal to mc 2 , and the energy of motion is always positive. This definition should be borne in mind when reading this article.Energy of interacting fields
Now we turn to the most elusive form of energy. The energy of a particle consists of the energy of a mass and the energy of motion. Remember that a particle is a field perturbation, that is, a well-defined wave.
 Fig. 1: a sketch of how the presence of a quantum of one field (blue wave) creates a disturbance in the second field (green), reaching the greatest intensity around the disturbance and decreasing to zero with distance.
Fig. 1: a sketch of how the presence of a quantum of one field (blue wave) creates a disturbance in the second field (green), reaching the greatest intensity around the disturbance and decreasing to zero with distance.But the fields are capable of doing a lot of things, not only generating disturbances. For example, a disturbance of one field can cause a non-wave change in another field. In fig. 1 I drew such a case - the blue wave-quantum of one field and the response of another field.
Suppose we have two particles — let them be perturbations of two different fields. In fig. 2 I marked them with blue and orange waves. Both of these fields interact with the green field. Then changing the green field will become more difficult. This is a sketch, not an exact reflection of what is too difficult to depict in the figure, but it gives an idea.
What is the energy of this system of two particles - two perturbations of two different fields and a third field interacting with both of them?
Perturbations are quanta, or particles. They have mass and energy of motion, and both of these quantities are positive.
 Fig. 2
Fig. 2The green field change also has some kind of energy. It is also positive, although often very small compared to the energy of the particles. It is often called the field energy.
But in the interrelations of various fields there is additional energy. Energy is there where the blue and green fields are strong, and also where the orange and green fields are strong. And so, what is strange. If to compare rice. 1 with fig. 2, there will be energy on both where the blue and green fields are strong. But the presence of nearby perturbations of the orange field changes the green field, and thereby changes the energy in the area where the blue field is located, as shown in Fig. 3
 Fig. 3
Fig. 3Depending on how the orange and green fields interact with each other, and how the blue and green fields interact, the change in energy can be positive or negative. I will call this change the interaction energy.
The possibility of negative changes in the interaction energy of the blue and green fields due to the presence of an orange disturbance (and vice versa) is the possibility that the interaction energy will be negative - the most important fact due to which all structures in the Universe can exist, from atomic nuclei to human bodies and galaxies. This is what is described below.
Earth and moon
The Earth is obviously not a particle. This is a huge set of particles, disturbances of various fields. But all of the above applies to a set of disturbances, not just one, and they all interact with gravitational fields.
Imagine the Earth by itself. Her presence creates a disturbance in the gravitational field (which, from the point of view of Einstein, is a distortion of local space and time, but this is not critical for us). Now place nearby the moon. It also distorts the gravitational field. And the gravitational field around the Earth changes due to the presence of the Moon. The details of how gravity interacts with the particles and fields that make up the earth ensure that the influence of the moon produces a negative interaction energy between the gravitational field and the earth. The reverse is also true.
That is why the Moon and the Earth cannot fly apart and remain trapped, tied together as tightly as if they were tied by a giant cable. If the moon were very far from the Earth, then the interaction energy of the system - the Earth, the Moon and the gravitational field - would be zero, not negative. But energy must be conserved. Therefore, in order to move the Moon farther from the Earth compared to its current location, it is necessary somewhere to take a huge amount of positive energy - in order to increase the negative interaction energy to zero. The moon and the earth have positive energy of motion due to motion in orbits, but it is not enough for them to scatter.
 Fig. 4: Absolute analogy with fig. 3
Fig. 4: Absolute analogy with fig. 3And besides pushing another planet with the Moon, there is no way to obtain such enormous energy, by chance or intentionally, from nearby sources. The power of all weapons accumulated by mankind is far from enough. Therefore, the Moon can not suddenly move away from the Earth - it is here for a long time, until some impressive catastrophe knocks it from orbit.
You may know that the theory of the collision of two objects the size of a planet — a large proto-earth and an object the size of Mars is considered the most popular theory of the formation of the Earth and the Moon. This theory explains the many complex puzzles associated with the moon. At the dawn of the solar system, high-energy collisions were definitely happening on a planetary scale, since the Sun and the planets formed more than 4 billion years ago! But there were no such clashes for a very long time.
The same logic explains why the artificial satellites of the Earth remain in orbit, why the Earth is tied to the Sun, and the Sun to the Milky Way, the city where a trillion stars live.
Hydrogen atom
On smaller scales and with less obvious consequences, an electron and a proton constituting a hydrogen atom remain connected to each other, unless there is energy from outside to change their state. In this case, the main work takes the electric field. In the presence of an electron, the interaction energy between the electric field and the proton (and vice versa) is negative. As a result, after you have formed a hydrogen atom from an electron and a proton (and waited a tiny fraction of a second until they are reduced to the preferred configuration, the ground state), the amount of energy needed to separate them will be about 14 eV. We call it the binding energy of hydrogen.
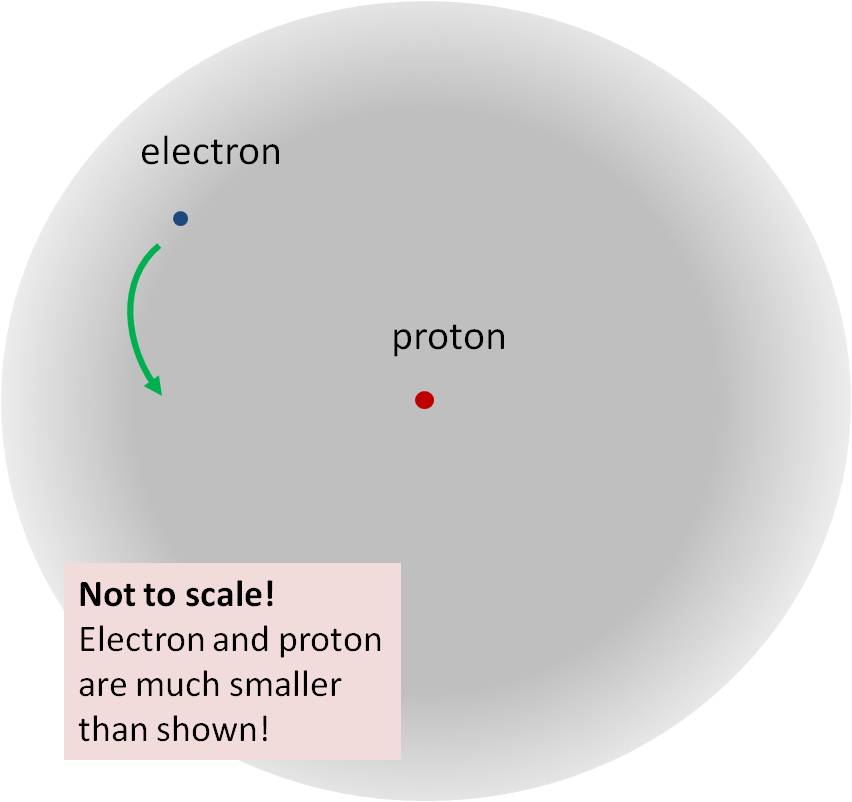 Fig. 5 ( not to scale! Electron and proton are much smaller). Inside the hydrogen atom, the electron disturbance propagates in the form of a cloud around a proton. The interaction energy, including the proton, electron and electron field, is -28 eV, it is partially compensated (mainly due to the energy of the electron's motion) and gives a binding energy of -14 eV.
Fig. 5 ( not to scale! Electron and proton are much smaller). Inside the hydrogen atom, the electron disturbance propagates in the form of a cloud around a proton. The interaction energy, including the proton, electron and electron field, is -28 eV, it is partially compensated (mainly due to the energy of the electron's motion) and gives a binding energy of -14 eV.We can measure the binding energy by shining ultraviolet light onto hydrogen atoms (photons with energy too large to see them with the eye), and seeing how large the photon energy must be in order to break the hydrogen atom. We can also calculate it using the equations of quantum mechanics - and the successful prediction of this quantity is one of the simplest tests of the modern theory of quantum physics.
But now I want to return to what I mentioned in the article about mass and energy, to one of Einstein's key ideas, acquired by him through working with the consequences of his equations. If you have a system of objects, then the mass of the system will not be equal to the sum of the masses of the objects contained in it. It is not even proportional to the sum of the energies of the particles contained in it. It will be equal to the total energy of the system, divided by c
2 from the point of view of the observer, resting relative to this system. (For a moving observer, the system will have more motion energy, not adding mass to the system). This total energy includes:
• Mass energy of particles (field oscillations),
• particle motion energy,
• Other sources of field energy, originating from non-wave disturbances,
• Field interaction energies.
What have we learned from the fact that 14 eV is necessary for the destruction of a hydrogen atom? Well, having broken this system, you will find yourself with a proton and an electron on your hands, which are far from each other and do not move particularly fast. At that moment the system energy will be:
• Mass energy of particles = electron mass energy + proton mass energy = 510 999 eV + 938 272 013 eV
• particle motion energy = 0
• Other sources of field energy, originating from non-wave disturbances = 0
• Field interaction energies = 0
But we know that before this, the hydrogen atom system possessed 14 eV less energy.
The electron mass energy is always 510 999 eV, and the proton energy is 938 272 013 eV, regardless of what they do. Therefore, the contribution of hydrogen mass energy to the total energy is the same as that of the electrons and protons divorced to the sides. You should get the following:
• The energy of movement of particles inside hydrogen,
• PLUS other sources of energy fields from non-wave disturbances (extremely small),
• PLUS field interaction energy,
• Should be EQUALLY binding energy -14 eV.
And if you do all the calculations, the figures are approximately as follows:
• particle motion energy = +14 eV,
• other sources of field energies from non-wave disturbances = extremely small,
• field interaction energies = -28 eV,
and the sum of all this will be equal to -14 eV.
There is no chance that the interaction energy is -2 * the energy of motion. Roughly speaking, this follows from the inverse square law for electric fields. Specifically, this follows from
the virial theorem .
What then is the mass of a hydrogen atom?
electron mass + proton mass + bond energy / c
2And since the binding energy is negative due to the large modulus and negative interaction energy, it turns out
This is one of the most important facts of the universe!
Why a hydrogen atom does not decay
Now I will tell you the same thing, but in a slightly different language, the language of particle physics.
Hydrogen is a stable compound consisting of a proton and an electron, connected through interaction with an electric field.
Why is it stable?
Any unstable object will fall apart. Decay is possible only if the sum of the masses of the particles into which the primary object decays is less than the mass of the initial object. This follows from the
laws of conservation of energy and momentum .
The minimal things that a hydrogen atom can break into are a proton and an electron. But the mass of the hydrogen atom is less (due to negative 14 eV of the binding energy) the sum of the masses of the electron and proton. Once again, this is important:
But hydrogen cannot decompose to anything else, therefore hydrogen cannot decompose at all.
All this works until the proton disintegrates, which, if it can happen, is extremely rare - we have never seen such an event. We already know for sure that this is such a rare event that not a single proton will disintegrate in your body during your life. So we will reject this opportunity.
The same is true for the remaining atoms. Atoms are stable because the interaction energy of electrons and atomic nuclei is negative. The mass of an atom is less than the sum of the masses of its components, so the atom cannot fall apart into electrons and a nucleus.
One catch: an atom can fall apart differently, as a result of the disintegration of the nucleus. And if a proton cannot decay (or does it extremely rarely), for most nuclei the situation is completely different.
And that brings us to important questions.
• Why is the neutron, unstable in itself, stable in the atomic nucleus?
• Why are some atomic nuclei stable and some not?
• Why is the proton stable, despite the fact that it is heavier than the quarks it contains?