Math gives us an accurate idea of almost exact answers.

Using heavy paper and transparent tape, Craig Kaplan collects a beautiful rounded object resembling the creation of
Buckminster Fuller or a fashionable new type of soccer ball. It consists of four regular dodecagons (12-gons with identical angles and sides) and 12 decagons (10-sided polyhedra) with 28 small apertures in the form of equilateral triangles. There is only one problem - this figure cannot exist. Such a set of polygons will not match the vertices, and the shape will not close.
The Kaplan model only works because when you collect it from paper, you have a little freedom of maneuver. The sides can bend almost imperceptibly. “The margin for error arising from working in the real world with paper means that those things that should not be possible are actually obtained,” said Kaplan, a computer scientist at the University of Waterloo in Canada.

This is a new example from a class of unexpected mathematical objects that the American mathematician Norman Johnson stumbled upon in the 1960s. Johnson worked on the completion of a project that Plato began more than 2,000 years ago - he created a catalog of ideal geometric shapes. Of the entire infinite variety of three-dimensional figures, only
five can be created from identical regular polygons: a tetrahedron, an octahedron, a hexahedron, an icosahedron, a dodecahedron. If you mix different regular polygons, you can compose 13 more figures in which all polygons meet vertices —
Archimedean bodies — as well as prisms (two identical polygons connected by squares) and “antiprisms” (two identical polygons connected by equilateral triangles).
In 1966, Johnson, working at the University of Michigan, discovered 92 more bodies, consisting only of regular polygons, which are now [in the USA] called
Johnson bodies . And this exhausted all the possibilities, which was proved several years later by the Russian mathematician
Viktor Abramovich Zalgaller , who was then working at Leningrad State University. It is impossible to compose any other closed shape from regular polygons.
But during the inventory of polyhedra, Johnson noticed something strange. He found his forms, making them models of cardboard and rubber bands. Since there are quite a few possible polyhedra, he expected that the new forms would appear rather quickly. If you start to make the edges together, then the figure must coincide. But this did not happen. “When assembling heaps of polygons, it was not always obvious whether I had assembled a valid figure,” recalls Johnson.
It may seem that the model has assembled, but “if you make calculations, it turns out that this is not quite the case,” he says. With careful study it turned out that what seemed square was not exactly square, or the sides were not completely flat. It would be possible to slightly cut the edges, and they would coincide ideally, but then it would no longer be regular polygons.
Having conceived to count all the ideal figures, Johnson did not attach importance to such “close hits”. “I put them off, and concentrated on the permissible,” he says. But these almost ideal figures not only attracted the attention of Kaplan and other lovers of mathematics, they became part of a larger section of almost ideal mathematics.
There is no exact definition of an “almost accurate” hit. Strict rules do not work in a tolerable world. Now Kaplan in the search for almost correct figures is guided by an approximate method: “a real, mathematical error inherent in a figure is comparable to a practical error arising from working with materials from the real world and with imperfect hands.” In other words, if you managed to assemble an impossible polyhedron - if it is so close to the possible that you can pass it off as a real one - then this will be an almost exact figure. In other sections of mathematics, almost exact results are so close to real that they can deceive or surprise you - a kind of mathematical joke.
Some such mathematical curiosities cannot be called anything more than simple fun, while others may have deep meanings in mathematics and physics.
The ancient problems of
squaring a circle and
doubling a cube fall into the category of almost correct solutions. They seem seductively open to finding the right solution, but in the end turn out to be impossible - like a geometric figure that looks closed, but it is not. Some designs, drawn by Leonardo da Vinci and Albrecht Durer, slightly bent the corners, giving almost regular pentagons as real ones.
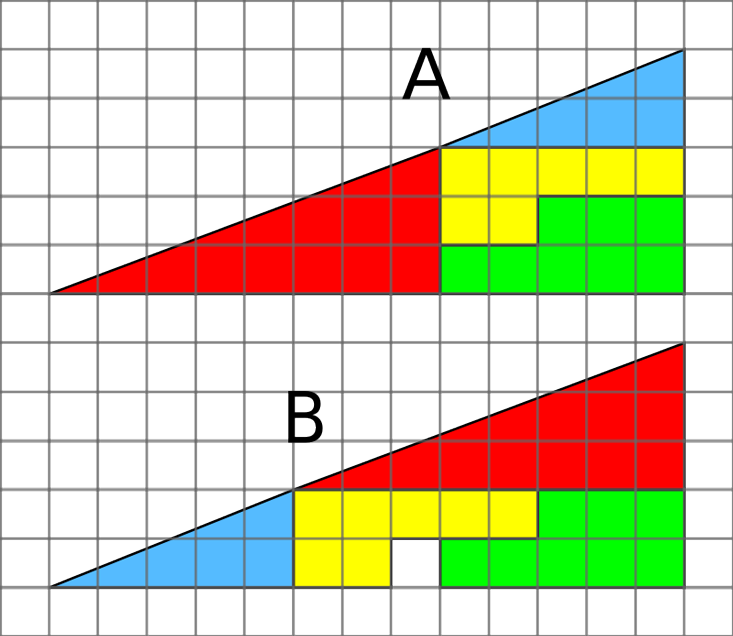
And there is also a riddle riddle. In the figure, a right triangle is cut into four parts. If you rearrange them in places, a gap appears in it. Where did he come from? This is also almost the right decision. None of the triangles is actually a triangle. Their hypotenuse is curved, and it is almost impossible to notice, which is why the illusion is so convincing.
Digital coincidence is one of the most useful, almost correct decisions in everyday life. 2
7/12 is almost equal to 3/2. For a similar reason, the piano has 12 keys in the octave and at the heart of the
evenly tempered structure of Western music. This is a compromise between the two most important musical intervals: an octave (2: 1 frequency) and a quint (3: 2 frequency). It is numerically impossible to divide an octave so that all fifths are perfect. But you can get close enough to this by dividing the octave into 12 semitones, seven of which will give you a frequency of 1.498. For most people, this is enough.
Sometimes almost accurate hits occur in mathematics as if she was deceiving herself. In the Simpsons episode "Treehouse of Horror VI", viewers interested in mathematics noticed something unusual: equation 1782
12 + 1841
12 = 1922
12 . At first glance, it may seem that the writers have refuted the Great Theorem Farm, postulating that the equation x
n + y
n = z
n does not have integer solutions for n> 2. If you enter these numbers into a pocket calculator, the result will seem to be right for you. But if you make calculations with an accuracy inaccessible to most pocket calculators, it turns out that the root of 12 degrees from the left side of the equation is 1921,999999955867 and not 1922, and the Farm can be calm. A surprisingly small slip of less than 10 ppm.
But such almost accurate hits are not just jokes. “Those that intrigue me more than others are cases that hint at the presence of something more significant,” says John Baez, a mathematician at the University of California at Riverside. This is the case of a value sometimes called the
Ramanujan constant. This number e
π √163 , equal to about 262,537,412,640,768,743.99999999999925, is surprisingly close to the whole. We cannot expect these three irrational numbers — e, π, and √163 — to somehow come together and give us a rational number, not to mention a whole. But there is a reason that they match so well. “This is not a coincidence of which we have no idea,” says Baez. “This is the key to the depths of mathematics.” The exact explanation is rather complicated, but it is based on the fact that 163 is the largest of the
Hegner numbers . The exponents associated with these numbers are very close to integers.
Or take a mathematical connection known as the “monstrous moonshine hypothesis” (monstrous moonshine). The story is this: in 1978, mathematician John McKay made as trivial as an interesting observation: 196,884 = 196,883 + 1. The first number was the coefficient of an important polynomial, a
j-invariant , and the second arose in connection with a huge mathematical object from group theory called "
Monster ". Many people would shrug their shoulders and go on, but this observation interested many mathematicians who decided to study it more closely. They found a connection between two seemingly unrelated topics: number theory and the symmetry of the Monster groups. This connection may have even broader, not yet open, consequences for other topics. Physicist Edward Whitten believes that the Monster group can be associated with quantum gravity and the structure of spacetime.
Mathematical almost correct hits show both playfulness and the power of the human approach to mathematics. Johnson, Kaplan, and others made discoveries with the help of trial and error — by studying the area as a biologist, plowing through the jungle in search of new species. But in mathematics it is easier to conduct a systematic search. For example, Jim McNeil, interested in mathematics as a hobby and collecting a collection of almost correct hits on his website, and Robert Webb, a programmer, created software for creating and studying polyhedra.
Almost accurate hits live on the blurred border between idealistic, rigid mathematics and our condescending and practical feelings. They turn the logic of approximation inside out. Usually the real world is considered an imperfect shadow of the world of Plato. The perfection of the underlying mathematics is lost in its implementation. But in the case of almost accurate hits, the real world is the perfect shadow of a non-ideal world. Approximation is "the wrong approximation of the correct answer," says Kaplan, and "almost accurate hit is an exact representation of an almost exact answer."
In this way, almost exact answers change the connection of mathematicians and mathematical physicists with nature. “I am grateful for the imperfections of the real world, because they allow me to achieve quasi-ideal by working with objects that are inherently imperfect,” says Kaplan. “They allow me to overcome the limitations of mathematics thanks to the beauty of a broken reality.”