1. A
ball on a spring, the Newtonian version2.
Quantum ball on spring3.
Waves, classic look4.
Waves, the classical equation of motion5.
Quantum waves6.
Fields7.
Particles are quanta8.
How particles interact with fieldsIn fact, some time ago we went to the territory of the fields, I just did not warn you about this - I wanted to concentrate on the waves arising on these fields. Describing how the waves behave, we expressed their shape and time dependence using the function Z (x, t). Well, Z (x, t) is a field. This is a function of space and time with the equation of motion that determines its behavior. A suitable motion function would be such that if Z increases or decreases at a certain point, then Z will decrease or increase at neighboring points a little later. This feature allows waves to be in the number of solutions of the equation.
In this article, we look at several examples of the fields Z (x, t), whose equations of motion allow the presence of waves. The physical interpretation of these fields will be very different. They describe the different properties of different materials. But the equations with which they are satisfied, and the waves that they demonstrate, will satisfy very similar mathematics, and they will also behave themselves, despite their different physical origins. This will be a very important moment in the future.
And then we will do something radical - consider the fields in the context of the special theory of relativity. As Einstein showed, if you correct space and time and force them to lead not in the way most people expect, you will receive a new type of field - such that its physical interpretation will not be a property of anything else, but an independent physical object.
Regular fields describing ordinary things.
The field Z (x, t) can represent a set of different physical quantities. For example:
• The height of the rope stretched across the room.
• The height of the water in the river.
• The density of the crystal or gas.
• The position of the atoms in the magnet.
• Wind speed.
• Temperature, density or air pressure.
In any of these cases, there is a field Z (x, t): height field, density field, orientation field, wind field, temperature field. Its value as a function of space and time tells us the height, density, orientation, wind speed or temperature of some environment - rope, river, crystal, gas, magnet, air - in all places at any time. His equation of motion shows how Z (x, t) can in principle lead. It also shows how to predict the behavior of Z (x, t) in the future, if we know for sure its behavior in the present and in the past.
In each example, there is a field and a medium, and we must not confuse the field with a medium. The field simply describes and characterizes one of the many properties of the corresponding medium. Very different environments can have very similar fields that behave with very similar waves - we'll see it later.
Once again, I will clarify the point, often causing confusion. In general, a field may have nothing to do with physical distance in space. Yes, in articles 3 and 4 I used the example of an ox on a rope to illustrate what Z (x, t) can be, because it is beautiful and intuitive. I also often built Z (x, t) graphics for waves. This may give you the false impression that Z (x, t) is always associated with waves that cause a physical object (such as a rope) to move a distance Z in the direction perpendicular to the x axis. But this is not the case, as three of our four examples will demonstrate to us.
Rope height field
First, consider our initial example of waves, the oscillating rope. In this case, the role of Z (x, t) is the height field, which we call H (x, t). It tells us the height of the rope at each point in space on the x-axis that runs along the rope, at any moment in time t. If the rope is at the equilibrium height H
0 , then H (x, t) = H
0 . The height field is a constant in space and time. If a simple wave moves through it, then the height field will be described by our famous wave formula from previous articles.
If we know H (x, t), we know the height of the rope at all points in space and time. If we know what the rope is doing now and what it did quite recently, with the help of the equation of motion we can predict what it will do in the future. This does not tell us much about the rope itself. The height field gives us only what its name implies: the height of the rope. A rope is a physical medium whose height is represented as a field H (x, t); it tells us nothing about the color of the rope, its thickness, tension, material, etc.
In fig. 1 I have made for you an animation of a wave in a height field going from left to right. It may seem that I painted the same thing twice, first green and then orange. But this is not the same thing. The orange curve is the rope itself, moving in physical space. The green curve is a graph that represents what is happening with H (x, t), regardless of what H (x, t) means (ie, height), or what kind of environment it is. And only in this case the green graph looks exactly the same as what is happening in the physical world. But in all other cases it will not be so.
 Fig. one
Fig. oneGrid Offset Field
Suppose we have a medium consisting of a crystal with atoms uniformly distributed at equal distances from each other. I drew them in pic. 2 in one dimension - one can imagine similar situations with three dimensions, but for now this would be an unnecessary complication. I also marked every 10th atom in red to make it easier for you to track their movement. And I also greatly exaggerated the distance between the atoms - imagine that there are several million atoms between every two red points, and not 10.
Let us look at the displacement field D (x, t), which tells us how much at time t the atom, usually located at the equilibrium point x, shifted from this point in the lattice. This means that in the case of a static state from which the animation begins, the field is zero everywhere, D (x, t) = 0, since all atoms are in their usual position. Then, in the animation, individual atoms begin to oscillate back and forth, and their motion, in general, spreads in the form of a wave going from left to right. At the top of the figure, the plot of the grid displacement field D (x, t) shows how the field behaves when a wave passes. Note that the fields in Fig. 1 and 2 behave in a similar way, despite the fact that the physical interpretation of the fields is very different.
 Fig. 2
Fig. 2Magnetic field orientation
What is a permanent magnet? It consists of a set of atoms, each of which serves as a tiny magnet with a tiny magnetic field, and all of them are aligned so that together they create a large magnetic field. The magnet is shown in fig. 3, and in it each atom is directed upwards. In this case, the orientation field Θ (x, t) tells us how far at time t the atom at the point x deviates from the vertical. Θ, in short, is the angle between the magnet of each atom and the vertical. Animation on fig. 3 shows a wave in a magnet in which the directions of the atomic magnets oscillate left and right. Above the green magnet shows the graph Θ (x, t); and again it looks exactly the same as in previous cases.

Air pressure field
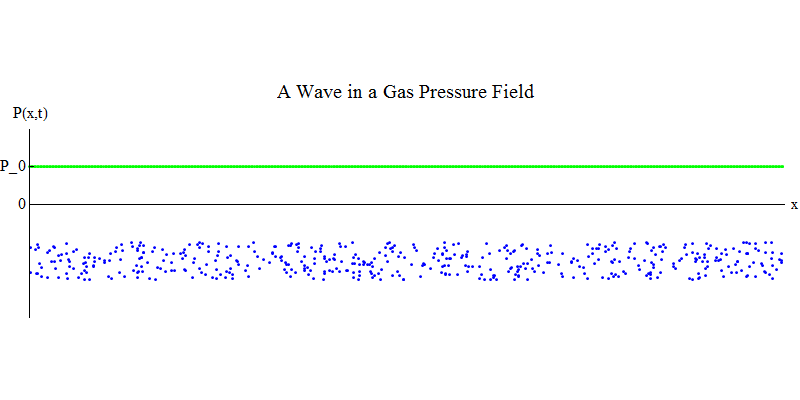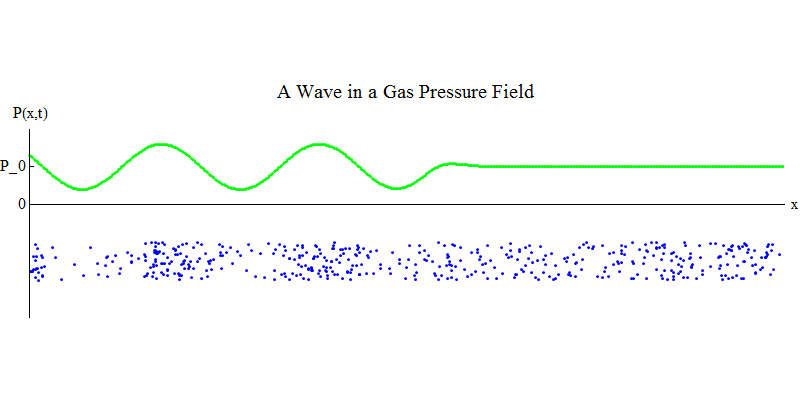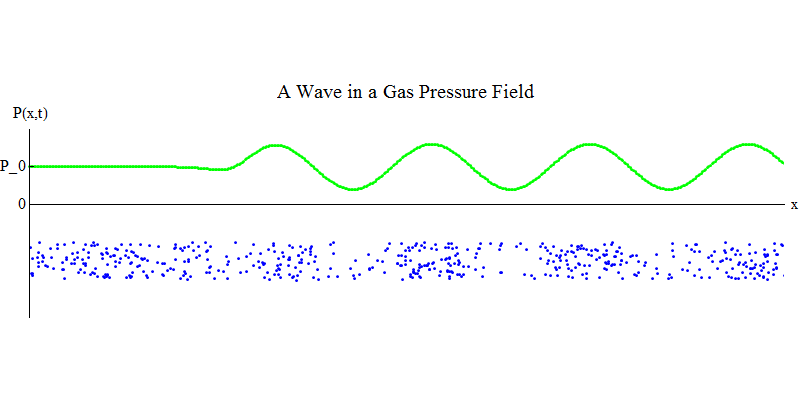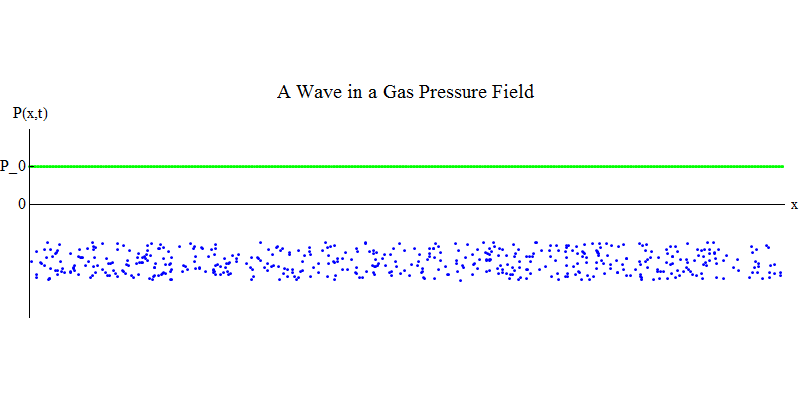
Consider a molecular gas in a long pipe. The dimension x will be located along the pipe. The gas molecules will move almost randomly, colliding with the walls of the pipe and with each other. In equilibrium, the density (the number of molecules in a certain volume) and the pressure P (x, t) (the force acting on the surface of a small ball that appeared at point x at time t) are constant. But the sound waves passing through the gas will cause the pressure and density to oscillate, as shown in fig. 4. Density and pressure periodically increase and decrease. Molecules move forward and backward, although on average they do not move at all, but at the same time the wave and its energy moves from left to right along the gas. The graph P (x, t) looks again very similar to the previous ones.
Important lessons
What can we learn from the four examples showing waves of class 0? (The equation of motion has one quantity, cw, and all waves in the corresponding field move at a speed cw. Different fields of class 0 will have different values of cw). We can learn that the same field behavior can appear from physically different fields that exist in physically different media. Despite their different origins, the waves in the height field, in the grid displacement field, in the magnetic orientation field and in the gas pressure field look identical in terms of the fields. They satisfy the same type of equation of motion and the same numerical relationship of frequency and wavelength.
Small print: strictly speaking, if you create waves of a fairly short length, you can still distinguish the behavior of different media. As soon as the wavelengths become equal to the distance between the atoms of the rope, or the crystal, or magnet, the wave equations that will be satisfied by the waves will be more complicated than those written by us, and their details will allow us to distinguish the media from each other. But often in practical experiments we do not even come close to observing such effects.
The result of this is that the study of the waves and their quanta associated with the fields does not necessarily tell you what serves as the medium, or what the physical interpretation of the field is - which of the properties of the medium it represents. And even if you somehow know that this is a field of a certain type - say, a pressure field - you usually still cannot say, based on its behavior, what pressure it represents. All that you can find out by studying the waves is whether the field belongs to class 0 or class 1, and what is its value of cw; or find out that the field belongs to another class.
In some cases it is very bad; The field conveys only partial information about the environment. Sometimes it is quite convenient; A field is a more abstract and universal piece than the physical material described by it.
Therefore, the field does not define the environment, and its behavior often does not depend on the details and properties of the environment. Because of what the question arises.
Can a physical field exist - with waves consisting of quanta moving in space and carrying energy - without any medium supporting it?
A field without a medium?
A song without a singer will not hear. But the song has some sort of independent existence; it sounds different, depending on who sings it, but there is something inherent in the song, some abstract quality, thanks to which you can always recognize it. This abstract entity is the melody of a song. We can discuss, study, learn a melody, record it with the help of a musical recording, without even hearing it performed by the singer. Many of us can even hum it in my head. Somehow the melody exists even if no one performs the song.
If in all the examples I have given and in all the examples I can give that will be intuitive to you, the field describes a property among, then how can a field exist without an environment? But somehow, the fields do not depend on their environment, since many different fields may behave in the same way, despite the fact that they describe many different properties of completely different environments. So it is probably possible to abstract the field from the environment.
In fact, it is not only possible, it seems to be necessary. At the very least, it is necessary either to have no environment, or to have an environment that cannot be created from ordinary matter, which is fundamentally different from all the considered media - in that it functions as follows (according to all the experiments), as if there is none .
One of several radical elements of Einstein’s special theory of relativity from 1905 was the idea that for light waves — decades considered waves in electric and magnetic fields (electromagnetic waves) and moving at the same speed in empty space — no medium exists. There are only fields.
The hypothetical medium was called "ether"; Einstein argued that such a thing does not exist, and wrote down a set of equations for which it was not required. I note that there is still a debate going on (often more philosophical than physical) about whether it is necessary or not necessary to imagine the existence of some strange environment that is very different from ordinary matter. To date, there is no evidence requiring its presence.
The key elements of the Einstein version of relativity (as opposed to the versions of Galileo and Newton) were the following:
• Space and time are not what you think they are. Different observers, moving uniformly relative to each other, will differ in their estimates of the length of objects and the time intervals between events (and these discrepancies can be accurately measured).
• There is a universal speed limit, with; any observer measuring the velocity of an object in relation to it will find that this velocity is less than or equal to c.
• In such a world, certain fields — “relativistic fields” —can exist without the environment, and they satisfy special equations of motion. The simplest relativistic field satisfies the equations of motion of classes 0 or 1, with the wave velocity cw, mentioned in the equation of motion taking the value c.
In short, there are relativistic fields of class 0 that satisfy the equation
Light, and all electromagnetic waves, is the most famous, but not unique example - therefore, "c" is often called the "speed of light." And there are relativistic fields of class 1 that satisfy the equation
We will see their examples in the next article. Note that relativity imposes no restrictions on μ (except for the need for μ
2 to be positive) or Z
0 . For relativistic fields, there are more complex equations, but most of them in the description of simple physical processes are reduced to one of these two.
Relativistic fields are physically real and have a physical meaning in the Universe, I mean:
• Their waves carry energy and information from one place to another.
• Waves in one field can affect another field and change the physical processes that would occur in their absence.
But, unlike the fields, examples of which are given in this article, relativistic fields do not describe the property of any ordinary physical medium consisting of something resembling ordinary matter, and, as far as experimentally known, they do not describe properties at all whatsoever that either. These fields, perhaps as far as we know today, are one of the fundamental elements of the Universe.