1. A
ball on a spring, the Newtonian version2.
Quantum ball on spring3.
Waves, classic look4.
Waves, the classical equation of motion5.
Quantum waves6.
Fields7.
Particles are quanta8.
How particles interact with fieldsSo we finally got to our goal: to understand what actually are those things that we call “particles”, namely electrons, photons, quarks, gluons and neutrinos. All this, of course, applies to modern science. It is worth remembering that in science there are no guarantees that the current understanding will not be further deepened.
The previous article described what fields are - objects that have meaning at any point in space and at any time (functions of space and time), satisfy the equation of motion, and are physically meaningful in terms of the fact that they are able to transfer energy from one place to another and influence the physical processes of the universe.
We have learned that most of the fields we are familiar with describe a property of the medium, such as rope height or pressure in gas. But we also learned that in Einstein's theory of relativity there is a special class of fields, relativistic fields that do not require a medium. Or, at least, if they have an environment, it is very unusual. Nothing in the field equations does not require the presence of some kind of medium and does not indicate what property of this medium is described by relativistic fields.
So for the time being, we will consider relativistic fields as elementary physical objects of the universe, and not as certain properties of an unknown medium. Whether such a viewpoint will be supported among physicists in the future, time will show.
We considered two classes of relativistic fields, and now we will study them in more detail. They satisfy either the Class 0 motion equation, where c
w = c (where c is the universal speed limit, often called the "speed of light").
Or Class 1 motion equations, where cw = c
The previous article showed that μ is the minimum frequency of a wave in such fields. In this article we will denote it by ν
min .
Why is the universal speed limit often called the speed of light? Waves with a class 0 equation move with a speed c
w . Light (the general term for electromagnetic waves of any frequency), moving through empty space, satisfies the relativistic equation of class 0, therefore the light waves (and waves of any relativistic fields that satisfy the relativistic equation of class 0) move with speed c.
Moreover, in the same article we saw that if a class 1 field has a wave with amplitude A, frequency ν, wavelength λ and equilibrium state Z
0 , then the equation of motion requires that the frequency and wavelength be related to the value μ = ν
min , appearing in the equations, the formula
This is the Pythagorean formula - it can optionally be represented as a triangle, as in fig. 1. The minimum frequency of any wave is ν
min , and the assignment ν = ν
min (and, therefore, as λ → ∞), corresponds to the compression of the triangle to a vertical line (Fig. 1, below). You can also get a similar ratio of class 0, making μ = ν
min zero. Then you can take the square root, and get
This is a triangle, compressed to a horizontal line (Fig. 1, right). In this case, the minimum frequency is zero. The field can fluctuate arbitrarily slowly.
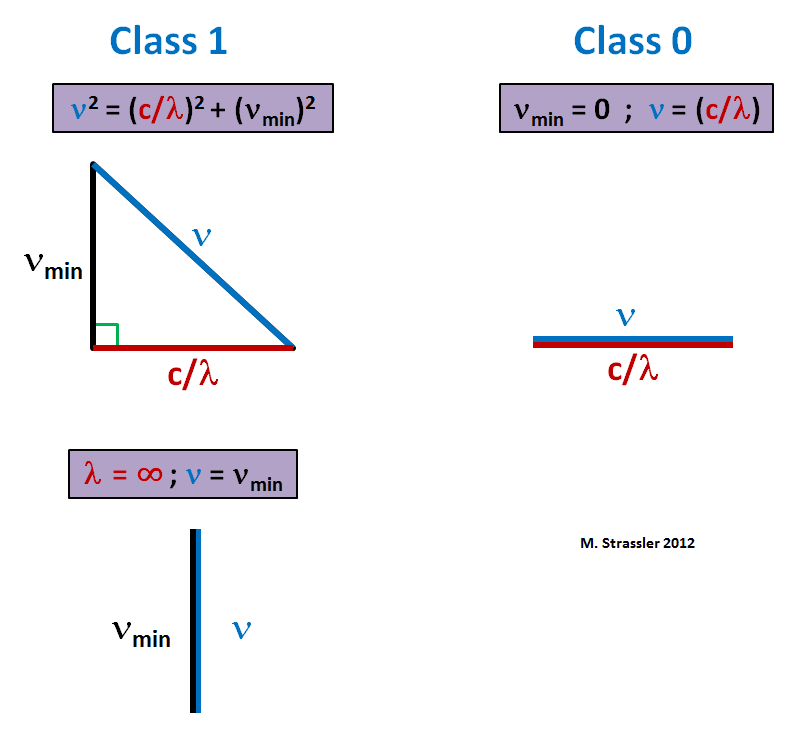 Fig. one
Fig. oneOn A there are no restrictions. But this is because we ignore quantum mechanics. It is time to study relativistic quantum fields.
Relativistic quantum fields
The real world is a quantum mechanical world, therefore the amplitude A cannot be any. It takes discrete values that are proportional to the square root of n, a non-negative integer that indicates the number of oscillation quanta in the wave. Wave energy is
Where h is Planck's constant, necessarily appearing where quantum mechanics matter. In other words, the energy associated with each quantum of oscillations depends only on the frequency of oscillation of the wave, and is equal to
This relationship was first proposed, specifically for light waves, by Einstein in 1905, in his explanation of the photoelectric effect.
But let us remember our Pythagorean ratio of frequency and wavelength. If we multiply it by h
2 , we get that for a quantum field class 1
Looks familiar. We already know that any object in Einstein’s theory of relativity must satisfy an equation describing its energy, momentum, and mass:
Another Pythagorean relationship. The minimum energy of the object is equal to mc
2 , which resembles the statement about the minimum frequency that a wave of class 1, ν
min can possess. We may be tempted to assume that, probably, for a quantum of a relativistic field
The first equation first appeared in the work of Louis de Broglie in 1924 - almost 20 years after Einstein. Why did it take so long? I dont know.
 Fig. 2
Fig. 2Does it make sense? As we noted, relativistic fields of class 0 include electric fields, and their waves are electromagnetic waves, that is, light. The version of formula (*) that we get for class 0 quanta is the same as for class 1 fields, for which μ = ν
min equals zero - that is, m = 0. We take the square root and get
Or the Einstein equation for massless particles. And quanta of electromagnetic waves (including all types of light: visible, ultraviolet, infrared, radio waves, gamma radiation, etc., differing only in frequency and, therefore, energy of quanta) and the truth will be massless particles - as soon as we apply this above a couple of equations (**) and (***). These are photons.
From equation (***) we can finally calculate the particle mass. Each mass possessing a mass is a quantum of a field of class 1. The minimum frequency of such waves is ν
min . The minimum energy of a single quantum of such a wave is h multiplied by the frequency. And the mass of a particle is simply the minimum energy divided by c
2 .
If we want to understand where the particle mass comes from, we need to understand what determines ν
min and why the minimum frequency exists at all. For particles such as electrons and quarks, this is completely unclear, but it is known that the Higgs field plays an important role in this.
We conclude: particles of nature are quanta of relativistic quantum fields. Massless particles are quanta of wave fields satisfying the equation of class 0. Possessing a mass correspond to the fields of an equation of class 1. There are many details, but this fact is one of the basic fundamental properties of our world.
Do these quanta really behave like particles?
We imagine particles as particles of dust or grains of sand. Quanta in this sense are not particles - they are waves that have minimal energy and amplitude for a certain frequency. But they behave so much like particles, that we can be forgiven for using the word "particle" in their description. Let's see why.
If you raise a wave in the water and allow it to pass through stones that lie shallowly beneath the surface, a part of the wave will cross the line of stones, and some will be reflected, as shown in Fig. 3. The exact part of the wave that crosses the line depends on the shape of the stones, their proximity to the surface, etc. But the point is that part of the wave is transmitted through the stones, and some will be reflected. A part of the wave energy will go in the same direction, a part will go in the opposite direction.
 Fig. 3
Fig. 3But if you send one photon in the direction of the reflecting glass, this photon will either pass through it or be reflected (Fig. 4). More precisely, if you measure the behavior of a photon, you will know whether it is reflected or transmitted. If you do not measure - it will be impossible to say what happened. Welcome to the quagmire of quantum mechanics. A photon is a quantum. His energy cannot be divided into the part that has passed through the glass, and the part that is reflected - because then there will be less than one quantum on each side, which is prohibited. (Fine print: glass does not change the photon frequency, so energy cannot be divided between two or more quanta of lower frequencies). So the photon, although it is a wave, behaves like a particle in this case. It is either reflected from glass or not. Whether it is reflected or not - this is not predicted by quantum mechanics. It only gives the probability of reflection. But she predicts that, whatever happens, the photon will travel as one and maintain its identity.
 Fig. four
Fig. fourAnd what will happen to the two photons? It depends. For example, if photons are emitted at different times from different places, the observer will see two quanta separated in space, and probably moving in different directions (Fig. 5). They may have different frequencies.
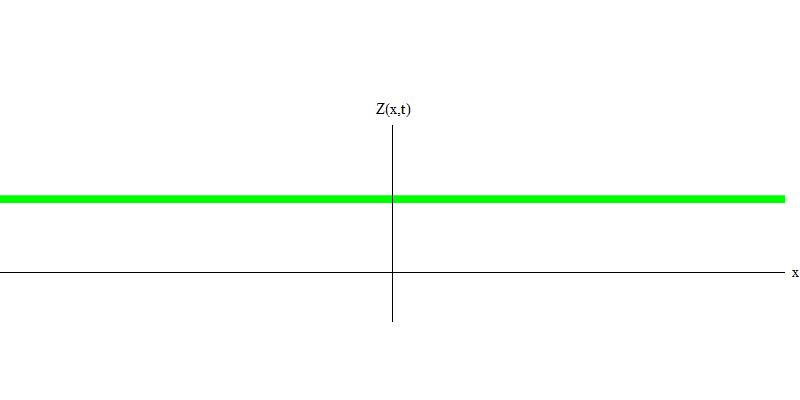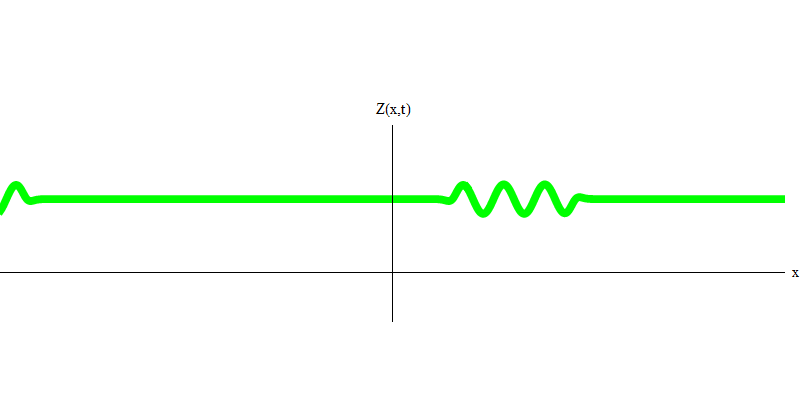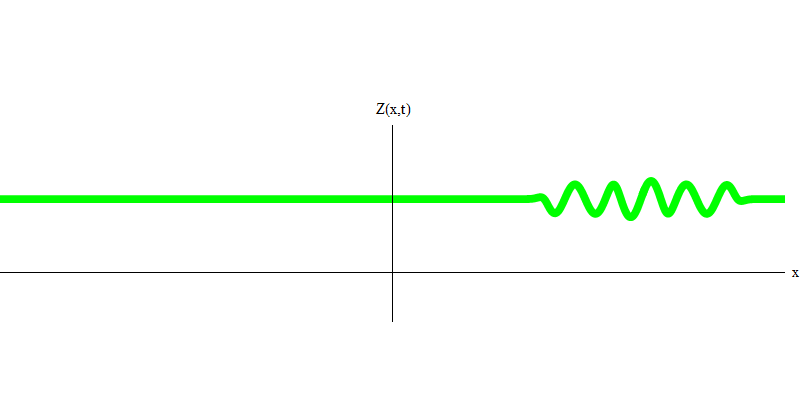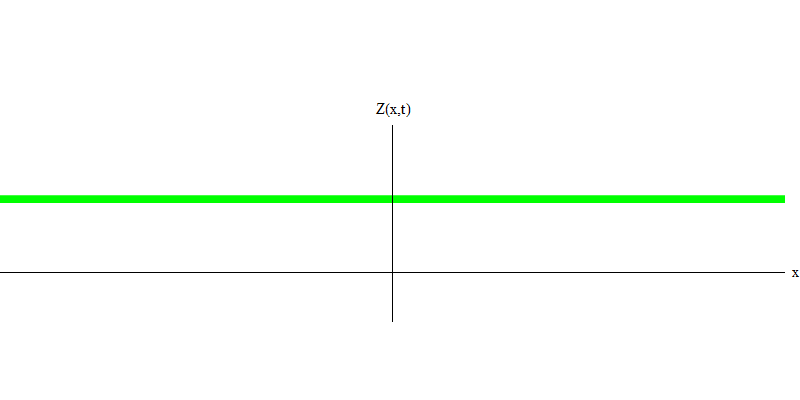 Fig. 5: independent quanta
Fig. 5: independent quantaIn the special case, when two photons are emitted together and ideally synchronously (as in lasers), they behave as shown in Fig. 6. If we send a combination of two photons on the glass, then not two, but three things can happen. Either both photons will pass through the glass, or both will be reflected, or one will pass, and the other will be reflected. 0, 1 or 2 photons will be reflected from the glass - there are no other options. In this sense, the light quanta again behave like particles, like small balls - if you throw two balls into the grid with holes, then 0, 1 or 2 balls will be reflected from the grid, and 0, 1 or 2 balls will pass through the holes . There is no possibility in which 1,538 balls will be reflected from the grid.
 Fig. 6
Fig. 6But these are photons, which, having no mass, are obliged to move at the speed of light and E = p c. What about particles with mass, like electrons? Electrons are quanta of the electric field, and, like photons, they can be emitted, absorbed, reflected or transmitted as a whole. They have a certain energy and momentum,
where m
e is the mass of an electron. The difference between electrons and photons is that they move slower than light, so they can rest. A sketch of such an event (in quantum mechanics due to the principle of uncertainty, nothing can be truly static) of a stationary electron is shown in Fig. 7. This is a wave of the minimum frequency, obtained by assigning a wavelength of a very large, almost infinite, value. Therefore, the spatial waveform in Fig. shows no convolutions - it just fluctuates in time.
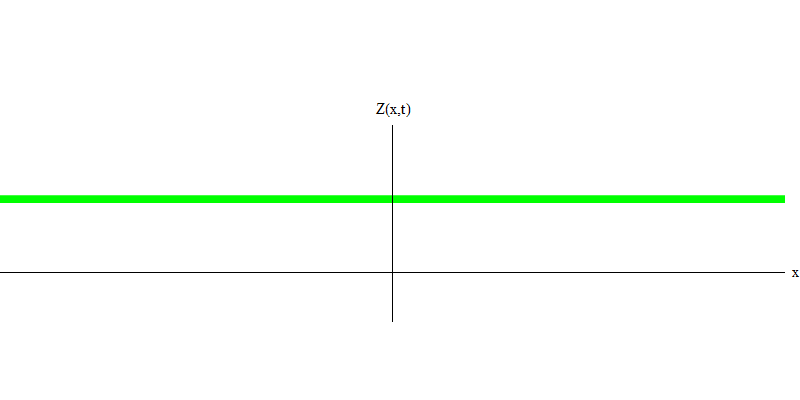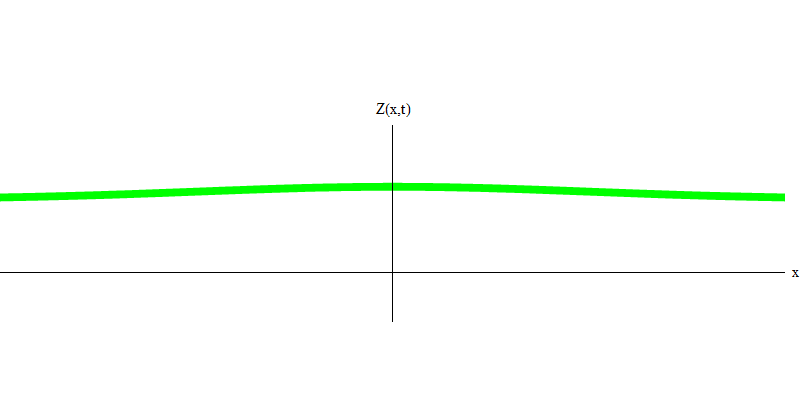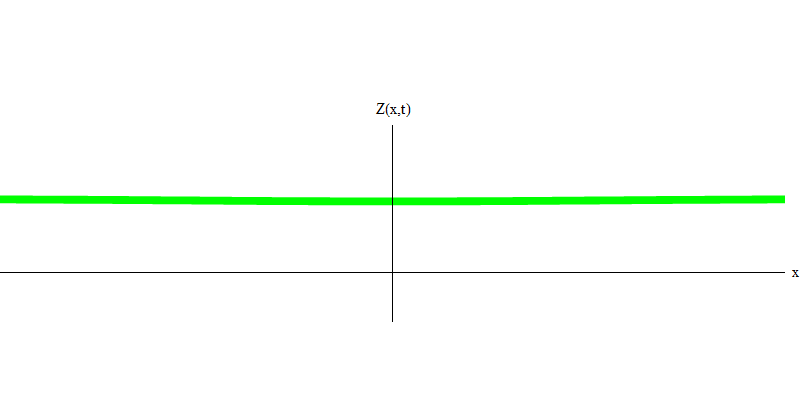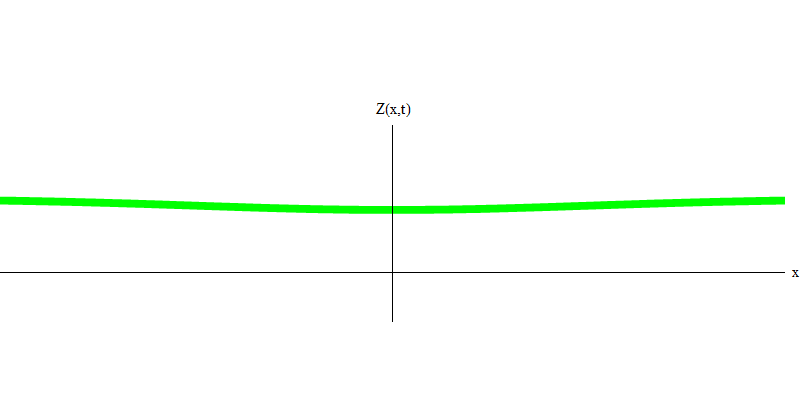 Fig. 7
Fig. 7So, yes, in fact, quanta behave very much like particles, and therefore calling electrons, quarks, neutrinos, photons, gluons, W-particles and Higgs particles “particles” will not be a catastrophic deception. But the word "quantum" is better suited for this - because it is precisely quanta.
How do fermions and bosons differ from each other?
• All elementary particles are divided into fermions and bosons.
• Fermions (including electrons, quarks and neutrinos) satisfy
the Pauli exclusion principle - two fermions of the same type cannot do the same.
• Bosons (including photons, W and Z particles, gluons, gravitons and Higgs particles) are different: two or more bosons of the same type can do the same thing.
That is why lasers can be made from photons - since they are bosons, they can be in the same state and generate a powerful beam of one light. But a laser cannot be made from electrons that are fermions.
How does this difference manifest itself in the language of mathematics? It turns out that the formulas I give are suitable for bosons, and for fermions they need to be changed — slightly, but with great consequences. For bosons we will have:
Which means that the energy of each quantum is h ν. This implies that quanta-bosons can do the same thing; when n is greater than 1, at the boson field the wave will consist of several quanta, oscillating and moving together. But for fermions:
The energy of a single quantum is still equal to h ν, so the entire discussion of particles and their energies, momentum and masses remains in force. But the number of quanta in an electron wave can only be equal to 0 or 1. Ten electrons, unlike ten photons, cannot be organized into one wave of greater amplitude. Therefore, there are no fermion waves consisting of a large number of fermions oscillating and moving together.