
String theory is often called the “theory of everything,” because its goal is to describe all the fundamental forces of interaction in the universe, including gravity, quantum mechanics, and relativity. This revolutionary concept represents a new understanding of space and time, it seeks to explain the connection of such phenomena as black holes and quark-gluon plasma, extra dimensions and quantum fluctuations.
Despite the complexity of the topic, Professor Steven Gabser of Princeton University offers a concise, accessible and entertaining introduction to this one of the most discussed areas of physics today. With a minimum of mathematics, using interesting analogies, the author explains the essence of supersymmetry, duality, the curvature of space-time so that it will be clear to any reader with a luggage of knowledge of high school.
While the provisions of string theory have not been finally proved, however, those secrets that have already been revealed to us allow us to admire the harmonious harmony of the universe and discuss the practical application of future discoveries in high-energy physics.
Gravity vs. Quantum Mechanics
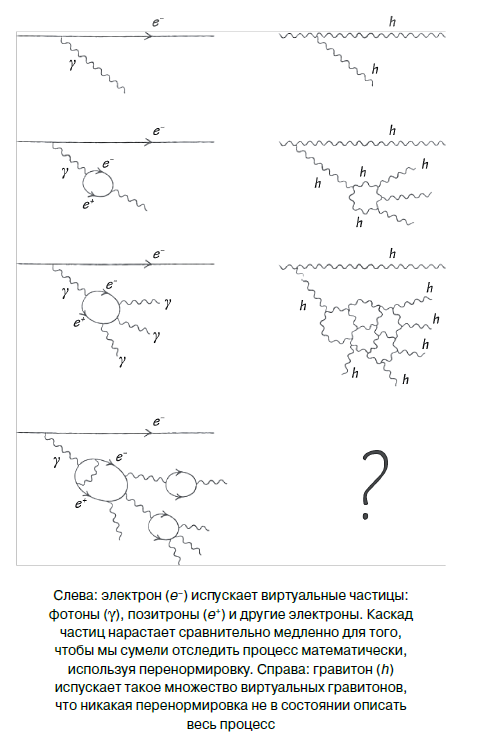
Quantum mechanics and the General Theory of Relativity - two triumphal physical theories that emerged at the beginning of the XX century - as it turned out, are not consistent with each other. The difficulty arises when applying the method called renormalization. I will talk about renormalization on the example of photons and gravitons, which we have already discussed in previous chapters. The point of inconsistency is that photons lead us to a renormalizable theory (which means “good theory”), whereas gravitons lead to a nonrenormalizable theory, and this actually means that we do not have a general theory describing photons and gravitons.
Photons interact with electric charges, but they are electrically neutral on their own. For example, an electron having an electric charge in a hydrogen atom, jumping from one energy level to another, emits a photon. This is what I mean when I say that photons interact with charges. The statement that the photon itself has no electric charge is equivalent to the statement that light does not conduct electricity. If this were not the case, you would get an electric shock each time, grabbing at an object that lay in the sunlight for a long time. Photons do not interact with each other; they only interact with electric charges.
Gravitons do not react to charges, but to mass, energy, and momentum. And since they carry energy, they interact with each other. It may seem that this is not a particular problem, but it is precisely because of this that we face difficulties. Quantum mechanics teaches us that gravitons behave like waves and particles. Particles are hypothetically point objects. And the point graviton will attract you the stronger, the closer you will be to it. Its gravitational field can be described as the emission of other gravitons. We will call the trial graviton maternal, and the gravitons emitted by it - children. The gravitational field near the parent graviton is very strong. So, its daughter gravitons possess huge energies and impulses. This directly follows from the uncertainty principle: the child gravitons are observed at a very small distance Δx from the parent graviton, and therefore, according to the uncertainty relation, Δp × Δx ≥ h / 4π, the uncertainty of their momentum, Δp, is very large. The trouble is that gravitons are also sensitive to momentum. Gravitons themselves will emit gravitons. The whole process branches and diverges incredibly quickly: you cannot take into account all the consequences of the interaction of all gravitons.
In fact, something similar happens near the electron. If you try to measure an electric field very close to an electron, then you will provoke it to emit a photon with a very large momentum. This seems harmless, because, as we know, photons do not emit other photons. The trouble is that a photon can produce an electron-positron pair, which then emits even more photons, which will generate new electrons and positrons ... A complete mess! The most amazing thing is that in the case of electrons and photons, you can nevertheless fully describe the whole set of particles cascaded from each other. Sometimes they talk about clothes, or “fur coat”, from the posterity, in which an electron is wrapped. Physicists use the term "virtual particles" to describe electronic progeny. Renormalization is a mathematical method that allows you to track all this mess.
The idea of renormalization is that a “bare” electron is assumed to have infinite charge and infinite mass, but as soon as we “put on” the electron, its charge and mass acquire finite values.
The problem with gravitons is that we are not able to renormalize the cloud of virtual gravitons surrounding it. The general theory of relativity - the theory of gravity - is nonrenormalizable. This may seem like a confusing technical problem: there remains a weak chance that we are simply looking at the problem from the wrong side. There is also an even weaker chance that the theory, called the Maximum Supergravity Theory, will be renormalizable. However, I and most string theorists are confident that there are fundamental difficulties in combining quantum mechanics and gravity.
Now let's take string theory. The initial assumption underlying it is that the particles are not pointlike. Instead, the particles are represented as vibrational modes of the string. According to the generally accepted idea of string theory, strings are infinitely thin, but of finite length (of the order of 10–34 meters) objects interacting with each other in the manner of gravitons. “Stop stop! - you protest. “But unless, in this case, general problems with a cloud of virtual particles — in this case, virtual strings — will not lead us to the same inability to track the whole process of interaction, as is the case with gravitons?” No. The fact that the strings are not point objects, kills the problem described in the bud. The source of difficulty in the case of gravitons is the assumption that they, according to the term "point particle", have infinitely small sizes. Replacing gravitons with oscillating strings smooths out the “sharp corners” of their interaction with each other. “On fingers” can be explained as follows: when a graviton gives rise to another virtual graviton, you can specify the exact place and time where it happened. But when a string forks, it looks like a branch of a water pipe.
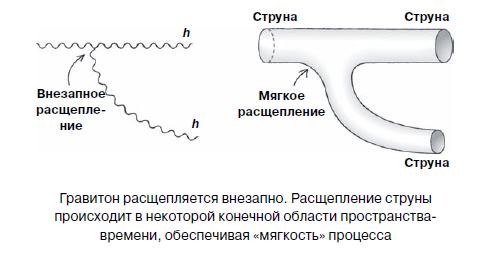
At the branching point there is no point at which a kink occurs, the Y-shaped figure illustrating this process looks like a smooth, continuous piece of pipe, only of unusual shape. All this leads to the fact that the division of the string is a more "gentle" process than the division of a particle. Physicists say that the strings interact by their nature “softly”, while the particles interact by their nature “hard”. It is this softness that provides the best behavior of string theory than the general theory of relativity with respect to the applicability of the quantum-mechanical description.
Strings in space-time
Recall in brief what we said about the vibrations of the piano string. If it is tight to pull the string between two pegs and strike it with a hammer, it vibrates with a certain frequency. Frequency is the number of oscillations per second. In addition to the fundamental frequency, the piano string also vibrates at overtones - vibrations of higher frequencies, which give the sound of the piano a distinctive color. I gave this analogy when describing the behavior of an electron in a hydrogen atom: it also has a fundamental oscillatory mode corresponding to the ground state with a minimum energy, and additional modes corresponding to higher energy levels.
The described analogy may not fully satisfy you: “Well, what does an electron in a hydrogen atom have to do with a standing wave on a piano string?” - you may ask. Most closer to the analogy with an infinitely small planetoid, orbiting around the tiny sun - the atomic nucleus, is not it? Is such a good analogy? Yes and no. Quantum mechanics argues that the idea of an electron as a particle and the idea of an electron as a wave are so deeply intertwined that the quantum-mechanical motion of an electron-particle around a proton can indeed be described as a standing wave.
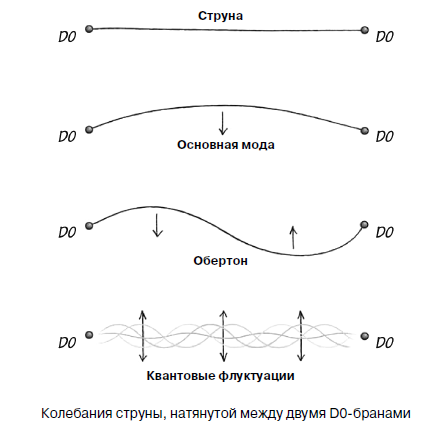
Comparing a piano string with strings that appear in string theory is actually a very correct method. To avoid confusion with different types of strings, I will call those strings that string theory deals with, “relativistic strings”. This term has a very deep didactic meaning, because string theory includes the theory of relativity, both special and general. Now I want to talk about one construction of string theory, which is so similar to a piano string, as much as a string can be like a string. Relativistic strings may end on objects that are called D-branes. If we omit the effects associated with the interaction of strings, the D-branes can be considered as infinitely heavy. The details of the D-branes will be discussed in the next chapter, and now I will only make a small digression, as it were, as a “crutch”. The simplest D-brane is called the D0-brane (pronounced "de-zero brane"). This is a point particle. I already hear the indignation of individual readers about the return to point particles: “Didn’t the author recently say that string theory aims to get rid of point particles?” Well, yes, that was until the mid-1990s, and then point particles again returned to string theory, and not alone, but led a whole zoo of unknown animals. But I am running ahead. All I want is to bring the string-theoretical analogue of the piano pegs that hold the string in the tensioned state - and D0-branes are so relevant in this role that I can not refrain from telling about them. In short, we stretch the relativistic string between two D0-branes, like a piano string between two pegs. The D0-branes themselves are not attached to anything, but they remain motionless because they have infinite mass. Funny is not it? All right, all right. About D0-branes - in the next chapter, and now - only about the stretched string.
The lowest energy level of the tensioned string corresponds to the absence of oscillations. Well ... almost absent, because small quantum oscillations are always present, and this fact is important. It is most correct to imagine the lower energy level as having a small vibrational energy in the framework of what is permitted by quantum mechanics. The excited levels of a relativistic string correspond to its oscillations either at the fundamental frequency or at the overtones of the fundamental frequency, and it can vibrate at several frequencies simultaneously, as well as the piano string. But, just like an electron in a hydrogen atom, a relativistic string cannot vibrate at an arbitrary frequency. An electron can choose energy levels from a discrete set. Relativistic strings are exactly the same. Different vibrational levels have different energies, and since mass and energy are related by E = mc2, different masses correspond to different vibrational states.
It would be great if I could say that the oscillation frequency of a string is related to its energy by a simple E = hν-type relationship, as was the case with photons. Unfortunately, it's not that simple. The total mass of the string consists of several components. The first of these is the rest mass of the string, which corresponds to the string tension energy between two D0-branes. The second is the mass corresponding to the vibrational energy, which in turn is made up of the vibrational energies of all overtones. I recall that energy and mass are related by the relation E = mc2. And finally, the third component is the mass corresponding to the energy of unavoidable quantum fluctuations, called zero oscillations. The term “zero oscillations” makes us remember the fundamental ineradicability of quantum fluctuations. So: the contribution of zero-point vibration energy to the string mass ... is negative! Granted, this is weird. Very strange. To show how strange it is, I will give this example. If we confine ourselves to one vibrational mode of the string, we will see that the energy of zero oscillations of this mode is positive. Each of the higher overtones separately makes an even greater positive contribution to the string energy. But if we sum up the contributions of all overtones accordingly, then we get a negative number. If you think that this is not bad enough, then here is even more bad news for you: I hid some of the truth, saying that the contribution of zero-point vibration energy is negative. All these effects - the rest mass, the energy of oscillations and the energy of zero oscillations - are included in the expression of the total mass by the squares of their values. And if the energy of zero-point oscillations prevails in this sum, the square of the total mass turns out to be negative, which means that the mass itself turns out to be imaginary, like the root of minus one.
Before you reject such nonsense with indignation, let me add that in string theory, a whole line of research is devoted to eliminating the described problem. In a nutshell, the problem is that the square of the mass of a relativistic string in its lower energy state is negative. Strings in this state are called tachyons. Yes, yes, these are the same tachyons that in each series confront the heroes of Star Trek. This is definitely bad news. In the model I described, one could get rid of the negative square of mass by dragging out the D0-branes to which the ends of the string are attached, far enough so that the string tension energy becomes more than the energy of zero oscillations. But when there are no D0-branes nearby, the string itself still remains. Deprived of her ability to attach herself to something, she can shut herself up. Now she is not stretched between something and something and can fluctuate, and maybe not. The only thing that it cannot stop doing is to fluctuate at the quantum level. And, as before, quantum vibrations turn such a string into a tachyon, which is very, very bad for a theory. According to modern concepts, tachyons are unstable, they are akin to a pencil balancing on the edge. You can try to balance such a pencil, but any light whiff will knock it over. String theory containing tachyons is reminiscent of the theory describing the millions of pencils standing on the tip, filling the space.
However, I too thick paint. There is a salutary solution for tachyons. Suppose that the imaginary mass and its square correspond to the ground state of the tachyon string: m2 <0. The vibrational energy also makes a certain contribution to the square of the mass. Using the correct deck and handing over the cards in the right way, you can ensure that the total mass of the string is exactly zero. This is encouraging because, as we know, in the real world there are massless particles, such as photons or gravitons. Therefore, if the strings really describe the real world, then they must be massless or, more strictly, at least some of the quantum states of the strings must be massless.
Please note that you need to take the correct deck of cards. With this metaphor, I wanted to say that we need 26-dimensional space-time. Perhaps you have already guessed that everything will come to this disgrace, so I will not apologize. There are several arguments in favor of 26 dimensions, but most of them are purely mathematical, and I am afraid that they will not seem convincing to most readers. The argument I give is more physical. We would like to get massless quantum states of strings. We know that quantum zero oscillations “push” m2 negatively. We also know that vibrational modes “push” m2 in the opposite direction. The minimum possible value of the oscillation energy does not depend on the dimension of space, while the magnitude of the quantum zero oscillations depends on. Let's look at it from which direction: when something fluctuates - the piano string or something else - it does it in a certain direction. The piano string oscillates in the direction in which the hammer hits it; for example, the piano string oscillates up and down, but not left-right. Swing chooses one direction and ignores the rest. In contrast, quantum-mechanical zero-point oscillations occur in all possible directions, and the addition of each new dimension adds one more direction to quantum fluctuations in which oscillations can occur. More possible directions of oscillation, or, as they are called, degrees of freedom, means a greater number of fluctuations, which leads to a greater negative contribution to m2. It remains only to calculate how to choose the right contributions to the total mass of vibrational modes and zero oscillations. It turns out that one oscillatory mode with the minimum energy value is compensated by a single 26-dimensional quantum zero oscillation. Look at it with optimism, because the number of necessary measurements could be non-integer! What would we do, for example, with twenty six and a half dimensions?
If you are not completely familiar with different types of vibrations, do not worry. They are very similar. The only difference between oscillatory modes and quantum zero oscillations is that oscillatory modes may or may not be present, while zero oscillations are always present. Zero oscillations are those minimal movements that are required by the uncertainty principle. In addition to the main mode, in the vibrations of the string there are overtones, giving the string new quantum mechanical properties. I prefer to imagine various modes in the form of simple mechanical models, such as circular oscillations, oscillations in the form of a clover leaf or torsional vibrations. Each form corresponds to a separate particle. In other words, the same string can play the role of different particles depending on the shape of the oscillations occurring on it. But to talk about the form of oscillations is still not entirely correct, because these oscillations are not mechanical, but quantum-mechanical. It is more correct to say that each particle has its own quantum mode. The geometric form is only a convenient way to visualize quantum-mechanical properties.
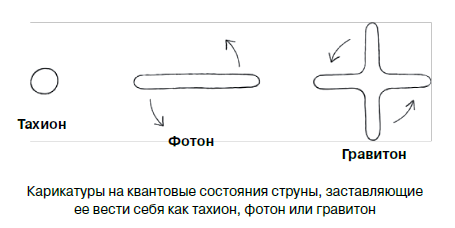
So we have: good news, bad news and very bad news. Strings, having different oscillatory modes, are able to behave like photons or like gravitons. It's a good news. They can only do this in a 26-dimensional space. This is bad news. In addition, there are oscillation modes that lead to imaginary masses and turn strings into tachyons, which introduce instability into the theory. More terrible than this news can not be.
The transition to superstrings allows to cure the theory of tachyons, and at the same time to reduce the number of necessary measurements from 26 to 10. In addition, superstrings allow a new type of vibrational mode, forcing them to behave like electrons. This is really cool. And if you could even come up with such super-duper strings, which would reduce the number of dimensions to four, you could open your own business to sell them. In this joke there is only a fraction of the joke. In reality, there is a variant of super-duper-string theory, called "string theory with extended local supersymmetry," which reduces the number of dimensions to four. Unfortunately, these measurements can exist only in pairs, that is, either four spatial dimensions are obtained and no single temporal, or two spatial dimensions and two temporal dimensions. In short, nothing good. We need three spatial and simultaneous measurements. Of the ten dimensions of the superstring theory are nine spatial and one temporal. One has to somehow get rid of six extra spatial dimensions in order to relate theory to the real world.
I would like to tell a lot about superstrings, but this story awaits its turn in the next chapters. Now I would prefer to dwell on the issue of the treatment of the theory of tachyons. Superstrings fluctuate not just in space-time, but in a much more complicated and abstract way. These special types of fluctuations allow you to solve the problem of tachyons, but not in the way you might have thought. Tachyons still remain in theory as one of the solutions for oscillatory modes with imaginary mass, but the trick is that if you consider modes that are responsible for the behavior of a superstring as a photon, graviton, electron or some other real particle, then no matter how you collide with these particles, no matter how they interact with each other, they never produce tachyons. Tachyons are possible, but they never arise. And this means that the theory still balances on the knife blade, but there is a special type of symmetry that helps maintain this delicate balance. This type of symmetry is called supersymmetry. Physicists hope to find experimental evidence for the existence of supersymmetry in the coming years. If they find them, many of us will believe in superstrings. But about this - in the seventh chapter.
»More information about the book can be found on
the publisher's website.»
Table of Contents»
ExcerptFor readers of this blog 20% discount on the coupon -
Strings