Understanding particle physics:
1. A
ball on a spring, the Newtonian version2.
Quantum ball on spring3.
Waves, classic look4.
Waves, the classical equation of motion5.
Quantum waves6.
Fields7.
Particles are quanta8.
How particles interact with fieldsHow the Higgs field works:
1.
The main ideaIn the
previous article in the series I explained that the particles of nature are quanta of relativistic fields that satisfy the equations of motion of class 0 and class 1. But what I haven’t said so far, so this statement, fortunately, is only partly true. Real equations are always slightly more complicated, so that the interrelation of particles and fields remains, but much more diverse phenomena and processes become possible, including the appearance of particles after the collision of other particles, the decay of particles into other particles, and the scattering of particles from each other, and also the formation of such interesting objects as protons and neutrons, atomic nuclei and atoms. I will not be able to explain all this in detail, but in this article I will give you an introduction to how it all works.
The key difference between the equations I called “class 0” and “class 1” and equations that are relevant to real physics is that there are additional terms in real equations that depend on two or more fields, and not just on one . That is, suppose, instead of the class 0 equation for the relativistic field Z (x, t), which looks like
for real fields, the equations look more like this:
Where y and y 'are numbers (usually less than 1), Z is a brief entry of Z (x, t), and A (x, t) and B (x, t) are a couple of other fields. In such equations, we can expect the appearance of such terms as A (x, t) Z (x, t), or A (x, t)
2 Z (x, t), or Z (x, t)
2 , or even A (x, t) d
2 Z / dt
2 , etc. Which members can and which cannot appear depends on the details of the fields involved in the process. The rules are strict, but rather confusing, so for now we will not delve into them. In general, from experiments we established (and understood from a theoretical point of view) that in nature:
• Any permissible term in principle (the conservation of electric charge or the correspondence of Einstein’s relativity) appears in the equations
• but members with many fields are usually very small and insignificant compared with members with one, two, and sometimes three fields (terms with time or space derivatives are also usually small).
Consequently, in most interesting physical processes, one can focus on all admissible terms with one, two, or three fields.
A bit of terminology. The terms in the equations with fields in the first degree are called linear. All terms in our class 0 or 1 equations were linear. Members with two or three fields are called quadratic or cubic; in general, they are called nonlinear. All interesting phenomena of our world appear due to nonlinear terms in the equations of motion - namely, the interaction of fields with each other and with themselves. Let's explore one of them.
The emergence of a new wave from the resonance of the other two
To get an idea of how interesting everything can be, take three fields, A (x, t), B (x, t), C (x, t), and a simplified situation. Suppose the fields A and B approximately satisfy the equations of class 0 (and contain massless quanta), and the field C satisfies the equations of class 1 (contains waves with a minimum frequency ν
min and, accordingly, quanta of mass m = h ν
min / c
2 , where h - Planck's constant). And we will add non-linear terms to their equations. Specifically, like this (for brevity, we will write “A” instead of “A (x, t)”, and so on, c is the speed of light, y is a number, usually less than 1):
The fine print: I added nonlinear terms to all three equations because the presence of such terms in one of the equations and their absence in the others will lead to contradictions; for example, energy will not be conserved. For the process I describe, we will need to consider only nonlinear terms in the equations of motion of the field C.
Let's see what happens with such a set of equations if the wave of the field A meets the wave of the field B. In principle, we can guess this by using the method of close scrutiny. If in the field A there is a wave, then A (x, t) is non-zero near it. When the waves of the fields A and B overlap each other, the result of multiplying A (x, t) and B (x, t) becomes non-zero. We now turn to the equation for C: changes in the field C in time and in space (two terms on the left side) are associated with the product A and B (one of the terms on the right side).
So even if the field C is zero, when A (x, t) B (x, t) becomes non-zero, then C (x, t) will soon become non-zero in the same segment. In short, as a result of the meeting of waves A and B, some small perturbation of the field C will occur.
The small print: you may be interested - after C becomes non-zero, whether the term A (x, t) C (x, t) in the equation of motion for the field B causes additional field perturbation B. The answer is yes, but this effect will be even smaller. While we ignore it, and later we find out why it was worth it.
In fig. 1 shows a wave with frequency ν in field A (green), occurring with a wave of frequency ν of field B (blue). I have equalized frequencies for simplicity and symmetry. We will see later why other cases boil down to this. The velocity ν can be estimated by observing the green wave and the vertical line located at one point in space and oscillating with the wave.
Below, the orange shows the product A (x, t) B (x, t); it can be seen that it becomes non-zero when two waves are superimposed. It also shows that it fluctuates over time. It can be seen (comparing it with an oscillating vertical line) that A (x, t) B (x, t) oscillates twice as fast. Remember this important fact. In the general case, if the wave of frequency ν
1 meets the wave of frequency ν
2 , then their product will oscillate with frequency ν
1 + ν
2 . And one more thing: you can see that the oscillations of the AV do not move to the right or left, they remain in place. We will see later why this is important.
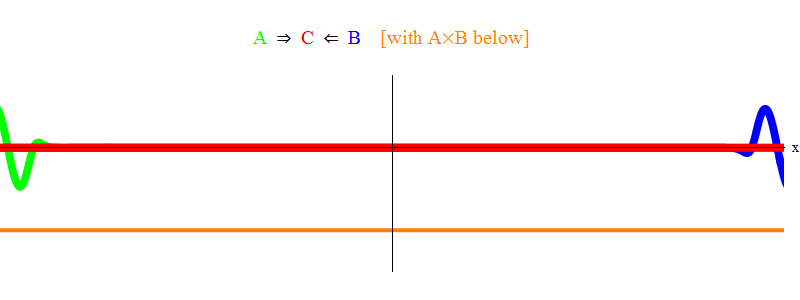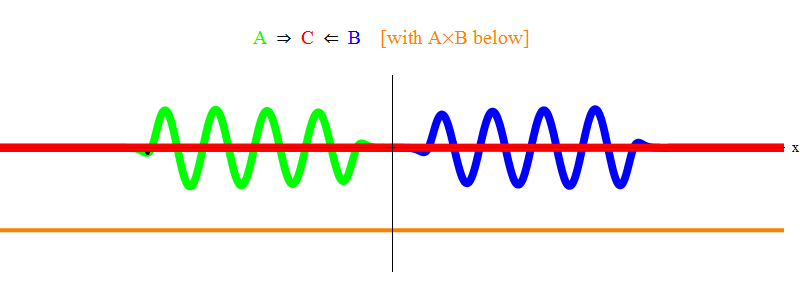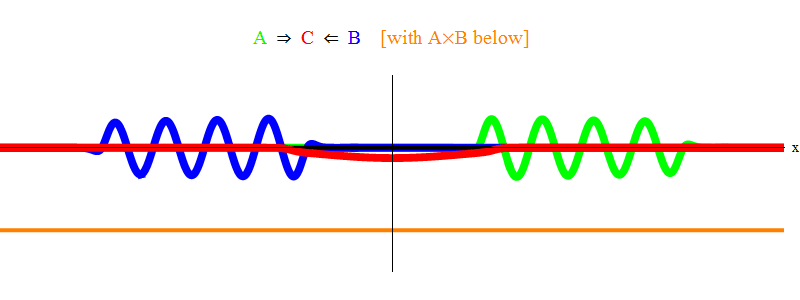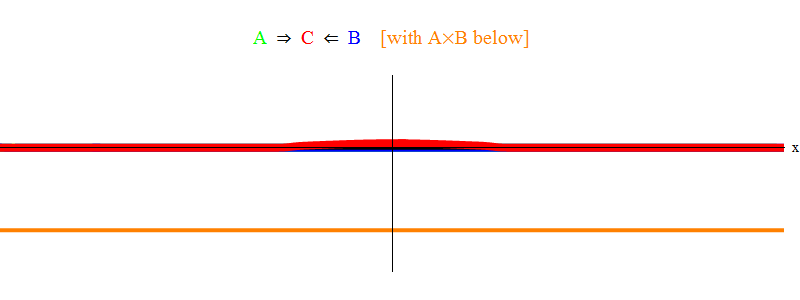 Fig. one
Fig. oneHow does a nonzero AB affect C? The answer strongly depends on the frequency ν. First, I will give you a ready answer, and then a rough explanation of the reason. This is, in fact, a
resonance . Resonance is an inherent phenomenon of all vibrations (vibrations), including waves. I have already described how a ball on a spring oscillates at a natural frequency, and how the oscillating force pushing a ball can lead to resonance if the frequency of the oscillation of the force coincides with the natural frequency of the ball on the spring.
Understanding resonance, you will see that field C, oscillating with a minimum frequency and zero horizontal velocity, behaves like a ball on a spring, and AB behaves like an oscillating force trying to make the ball oscillate. Therefore, the phenomenon of resonance occurs if the oscillation frequency of the AV - 2ν - is the minimum frequency of the field C - ν
min . More specifically:
• If 2 ν is not equal to ν
min - if the forces are not in resonance - then in the area where AB is not zero, C will begin to oscillate irregularly, with a small amplitude.
• If 2 ν = ν
min - if the force is in resonance - then C will oscillate smoothly, with a large amplitude, on the section where AB is not zero, and continue to oscillate even when AB again becomes equal to zero.
Fig. 1 shows only the resonance situation 2 ν = ν
min . It can be seen that when wave A passes wave B, they leave behind them a stationary wave C, oscillating at a frequency of ν
min . Small font: in fig. Shown is a sketch, not an exact solution to the equations. The exact solution will have many small complex features that will overshadow the basic physical meaning, so I removed them for clarity. Later we will consider a situation without resonance, which is much more complicated, but also more important for physics.
The emergence of a new particle from the annihilation of the other two
I just showed you that the nonlinear AB terms in equation C can cause the imposition of waves A and B to generate oscillations of field C if the sum of the frequencies of the fields A and B is equal to the minimum frequency of the field C. But what if these waves had very small amplitude? What can happen if one quantum of field A encounters one quantum of field B?
• If AB frequencies enter into resonance with field C, then a quantum of field C may appear, that is, a real particle C, and quanta A and B will disappear - “annihilate”.
• Also, quanta A and B can simply pass past each other, without creating particle C.
• The laws of quantum mechanics suggest that the probability of creating a particle C is proportional to the square of the number y, which is multiplied with AB in the equation of motion C.
• If the frequencies do not enter into resonance, the real particle C will not appear. However, a temporary disturbance may occur in the field C, an example of what is often called a “virtual particle” C, in which case quanta A and B may disappear. What is the result of such a disturbance? I partially described this process at the end of the article, in the “tails” section.
This is the general situation. Let's get into the details.
What for particles, that is, quanta of fields A, B and C means to be in resonance or not in resonance? It is worth remembering that the quantum energy is related to its frequency due to the equation E = h ν. So we will translate our discussion of waves into a discussion of particles.
Suppose that our waves in the fields A and B are each of one quantum. These quanta are massless, since A and B satisfy the equations of class 0. More precisely, the linear terms in their equations of motion are the same as the equations of class 0. Since quanta A and B have one frequency, they have the same energy, E = h ν. Since the momentum of a massless quantum is p = E / c, quanta A and B will have pulses equal in magnitude to h ν / c, but opposite in direction, since one of them moves to the left and the other to the right. Consequently:
• The total energy of two quanta together will be 2hν.
• The total momentum of two quanta together will be zero.
Since the energy and momentum are conserved, the total energy after a collision of two quanta will remain equal to 2hν, and the total moment remains zero.
In the case of waves, we have seen that since the equation for C contains a member of the form AB, there is a resonance when the frequency AB (working as an oscillatory force) coincides with the minimum frequency C (working as a ball on a spring). Let's translate this statement into quanta.
The frequency AB will be 2 ν, so the energy of the product A and B, when the waves A and B consist of one quantum, is equal to the sum of the energies A and B.
The minimum frequency C is ν
min , which means that for a stationary quantum field C the pulse is 0, and the energy
Where m is the mass of quantum C.
Resonance requires 2 ν = ν
min , that is:
In short, resonance occurs when the sums of equal energies of particles A and B (which are identical in magnitude and opposite in direction to the pulses in our case) are just enough to create a stationary particle C! In the process, the particles A and B are annihilated - their energy completely goes into creating particle C. This is shown (schematically) in fig. 2, which you need to compare with Fig. one.
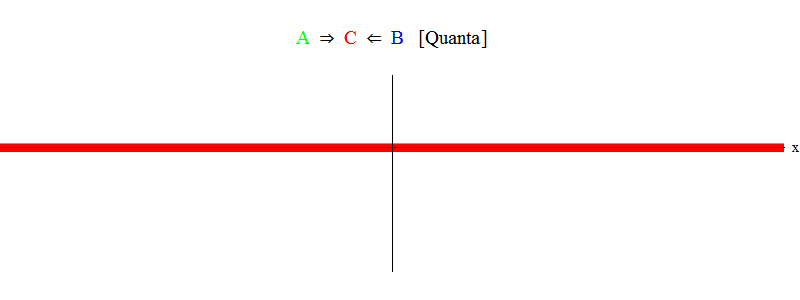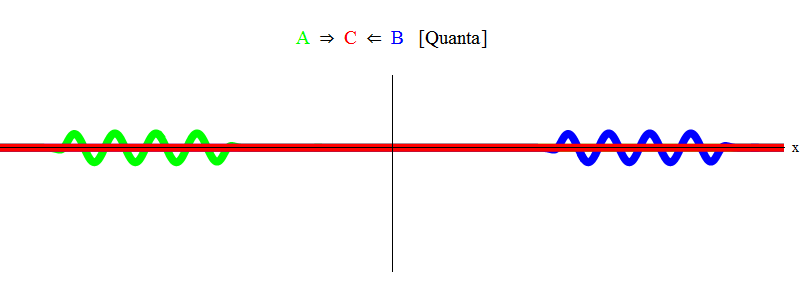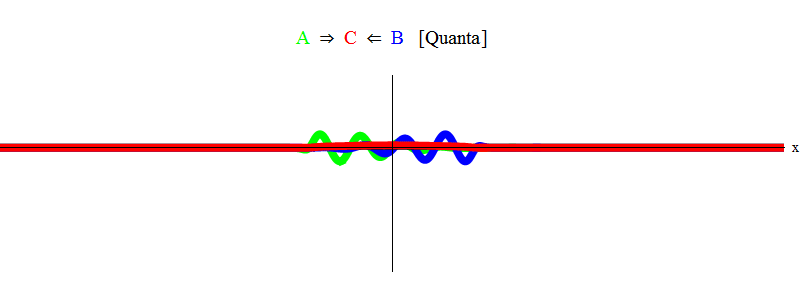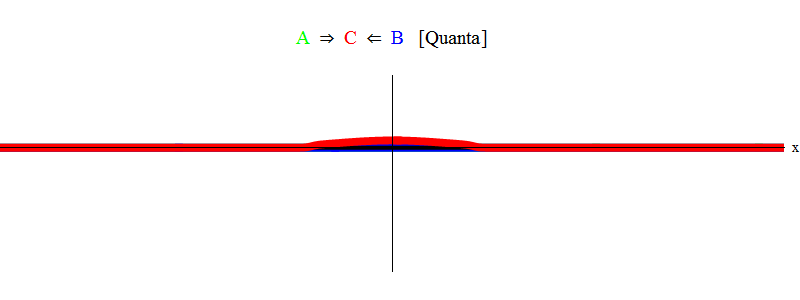 Fig. 2
Fig. 2Reasoning
I just showed you the A + B → C process. In my explanation, I used three different types of particles to avoid confusion. But the same idea allows processes like A + A → C to pass (for example, gluon + gluon → Higgs particle, and basically this is how a Higgs particle is obtained at the Large Hadron Collider) and processes like A + A * → C, where A * - antiparticle for A (for example, quark + antiquark → Z-particle, and this is how Z-particles usually get at the LHC). It is only necessary to change minor details, but the essence remains the same.
Another process that represents the same idea, but reversed in time - the decay of particles. The decay of the Higgs particle into two photons or Z-particles into a quark and an antiquark in essence occurs in the same way as the animation in Fig. 2, going in the opposite direction.
Tails
1. If the term AB perturbs the field C without a resonance — if 2 ν ≠ ν
min — what happens? You may remember that if you push a swing with a child with the wrong frequency, or apply a force on a ball on a spring, which oscillates with a frequency that does not coincide with its own frequency of oscillation, you will get an uneven oscillation with a small amplitude. In the current context, the same thing happens with the field C. The field C will somehow behave, but this will not lead to the appearance of a well-behaved quantum C. It will just wane a little. This is a bad indignation - one of the examples of the so-called. “Virtual C particles” - but this is not a particle (quantum of the C field wave), despite its name. Its mass is different from the mass of particle C; it may be larger or smaller. Unlike particle C, it does not exist by itself for some long time. And it does not satisfy the conditions in amplitude that real quanta should satisfy. Instead, in contrast to the existing C particle from Fig. 2, a non-resonant perturbation exists only when A intersects with B.
But this does not mean that it does not affect anything. For example, it can cause particles A and B to bounce apart.
In general, in three-dimensional space, rebound, or scattering, can lead to A moving in any direction, and B moving in the opposite direction. Examples of such processes include electron and positron scattering due to a virtual photon, or quark and antiquark scattering due to a virtual gluon.
In the presence of other fields, D and E, interacting with C and participating in the equation of motion C
Much more interesting processes can occur:
A + B → C
perturbation → D + E
That's right: particles A and B can annihilate thanks to a virtual particle C, and lead to the emergence of new particles D and E. This is the second way to create new particles! For example, an electron can collide with a positron, annihilate through a virtual photon (remember, this means “through the perturbation of the photon field at a frequency that does not coincide with the resonant one”) and turn into a muon and antimuon, or a quark and antiquark. The lower quark and the upper antiquark can collide, annihilate through a virtual W-particle, and turn into an electron and antineutrino. Or two gluons can collide, annihilate through a virtual gluon, and turn into an upper quark and an upper antiquark (this is the most common way to obtain upper quarks at the LHC).
2. What if two waves in fields A and B have different frequencies, ν
A and ν
B ? At suitable frequencies, particle C may still appear, but the resonance conditions will be different, and the particle C created will not be stationary. Let's figure it out.
If they have different frequencies, the two colliding massless quanta will have
• Different energies
and
• Various impulses
and
(here plus means to the right, minus - to the left).
The total momentum p
A + p
B is now non-zero. But the momentum is maintained. Therefore, if a particle C can arise as a result of the annihilation of particles A and B, it will have an impulse p
C = p
A + p
B , therefore it will move to the left or to the right, and not stand still. If ν
A > ν
B , then it will move to the right, otherwise - to the left.
How much energy is required to create a moving C particle? To do this, you need more energy than for the resting - like any massive particle, its energy and momentum must satisfy
Which means that E
= mc
2 , if p
= 0, or more, if the impulse is nonzero. The law of conservation of energy and momentum tells us that:
Where did I get the last equation? For a massless particle, p = E / c, and for our colliding particles A and B, their momenta are opposite, so they differ in sign. Substitute it in the previous equation and get:
The members of E
A 2 and E
B 2 are mutually destroyed, and transferring the members of E E E
B to the left side, we get:
Dividing by h
2 and using the relation m = hν
min / c
2 , we obtain the resonance condition:
What is correctly reduced when ν
A = ν
B , to the equation for a stationary particle C, 2 ν = ν
min . If this condition is not satisfied, then particle C cannot be created. If satisfied, then you can.
3. I noted that in the same way as the equation of motion for the field C contains a member AB, so the equation for B contains the member AC. Recall these equations:
So, if the imposition of waves A and B leads to the appearance of a wave in the field C, making it non-zero, as in Fig. 1, do we need to worry about the fact that this new wave C will overlap the existing wave A and lead to a change in field B? I replied that "yes, but we can neglect this." We can ignore because of a combination of two reasons.
Firstly, because of the number “y” appearing before the multiplications AB and BC. The impact on the field C of the member AB is proportional to y multiplied by A multiplied by B. The impact on the field B of the member AC is also proportional to y multiplied by A multiplied by C, but this in turn will be equal to y
2 multiplied by A multiplied by A multiplied by B. So while y is less than 1, y
2 is less than y, therefore the effect on B of the member of the AU is small compared to the effect on C of the member AB - at least for small waves A and B. In practice, these waves are usually small: particle A is one quantum wave in field A, so wave A has small amplitudes d.
From which follows a second, more strange, but more convincing reason: we have seen that if one quantum A encounters one quantum B and turns into one quantum C, then waves A and B disappear (they annihilate). After creating C, there is already no wave A, therefore the AU is zero, that is, there is no impact on field B.
And the last catch: although I can’t prove it without additional calculations, even if A and B have waves of one quantum, as in fig. 2, the process in fig. 2 would be much more complicated if y were much more than 1. So the simplicity of the story I told requires small values of y. In nature, most nonlinear terms in particle physics are usually small, so what I have said applies to most practical situations. Exceptions are very interesting - they lead to the creation of such complex objects as protons and other hadrons.