
Physics is the most complex complex science, it is as complex as it is fascinating. If we drop the mathematical component, physics immediately becomes accessible to anyone with curiosity and imagination. We can easily understand the concept of the theory of gravity, dispensing with complex mathematical equations. Therefore, anyone who thinks about what makes blueberries blue and strawberries red; who doubts that sound propagates in the form of waves; who is interested in why the behavior of light is so different from any other phenomenon in the Universe, it is necessary to understand that the whole thing is in quantum physics.
This book presents (and demystifies) to ordinary people the magic world of quantum science, like no other book. She talks about basic scientific concepts, from light particles to states of matter and the causes of the negative influence of greenhouse gases, revealing each topic without using specific scientific terminology - examples from ordinary everyday life. Of course, a book on quantum physics cannot do without a minimum set of formulas and equations, but this is a necessary minimum, understandable to most readers. According to the author, a book that popularizes science should be accessible, but not fall to the level of the reader, but raise and develop its intellect and general cultural level.
Quantum Racquetball and Fruit Color
The key property of electrons bound to atoms and molecules is that their energy states are discrete. We say that the energy of an electron can be quantized, that is, an electron bound to an atom or molecule can have only some specific energy values. The energy varies in steps, and these steps have certain discrete dimensions. Energy states are like stairs. You can stand on one step or go up to the next, higher step. However, it is not possible to stand halfway between two steps. These discrete, or quantized, energy values are often called energy levels. Unlike conventional ladders, the intervals between energy levels are usually not the same.
An important area of modern quantum research is the calculation of the electron states of molecules. This area is called quantum chemistry. Such calculations allow one to obtain quantized energy levels for electrons in molecules (energy levels), as well as to calculate the structure of molecules. The calculation of the structure of the molecule gives the distance between atoms and the position of all atoms in the molecule with an accuracy limited only by the uncertainty principle. Thus, quantum mechanical calculations allow us to determine the size and shape of molecules. Such calculations are important for understanding the fundamental principles of binding atoms into molecules and for constructing new molecules. With the development of quantum theory and the emergence of more and more powerful and complex computers capable of solving time-consuming mathematical problems, larger and larger molecules can be investigated using quantum chemistry methods. One of the most important applications of quantum theory is the development of pharmaceuticals. Molecules can be designed so that they have the desired size and "fit" in shape to specific loci of proteins or enzymes.
Quantum chemistry requires very time-consuming calculations. Even for the simplest hydrogen atom, quantum mechanical calculations are very complex mathematically. The hydrogen atom consists of one electron bound to one proton. The proton, which is the nucleus of the hydrogen atom, is a positively charged particle, and the electron is negatively charged. The attraction of a negatively charged electron to a positively charged proton holds them together, pinning a hydrogen atom. Details of the calculation of the energy levels of the hydrogen atom will not be presented here, but in the following chapters we will look at some of the features of the results of these calculations. They give the energy levels of the hydrogen atom and its wave functions. It is the wave functions, that is, the probability amplitude waves for a hydrogen atom, are the starting point for understanding all atoms and molecules. Atoms and molecules are complex because they are absolutely small three-dimensional systems, and it is necessary to take into account how protons and electrons interact with each other.
A particle in a box - a classic case
There is a very simple task related to our topic. It is known as the particle problem in the box. Solving this problem does not require complicated mathematics, but this solution allows us to illustrate important properties of bound electrons, for example, quantization of energy levels and the wave-like nature of electrons in bound states. Before analyzing the nature of an electron in a one-dimensional box of atomic dimensions, we discuss the classical problem of an ideal one-dimensional playground for racquetball, in order to identify the differences between the classical (large) and quantum-mechanical (absolutely small) systems.
In fig. 8.1 shows the perfect "box". He is one-dimensional. Its walls are considered infinitely high, infinitely massive and completely impenetrable. There is no air inside the box that would resist movement. In the figure, the inside of the box is designated Q = 0, and the outside is Q = ∞. Earlier it was said that a particle is called free such that no force acts on it. Forces arise when a particle interacts with something. For example, a negatively charged particle, such as an electron, can interact with a positively charged proton. The interaction in the form of attraction between oppositely charged particles will generate a force acting on the electron. When controlling electrons in a CRT (see Fig. 7.3), the electric field generates a force acting on the electrons and forcing them to change direction.
A measure of the interaction of a particle with something affecting it, like an electric field, is called a potential and has the dimension of energy. In the future, the potential will be denoted by the letter Q. Inside the box, Q = 0, as in the case of a free particle. This means that the particle does not interact with anything inside the box. There are no electric fields or air resistance. However, outside the box Q = ∞. Infinite potential means that the particle would have to have infinite energy to be in areas outside the box. The expression Q = ∞ is simply a way of formalizing the statement that the walls of the box are perfect. A particle cannot penetrate through the walls or jump over them, however great its energy may be. If you place a particle in such a box, it cannot slip away and will always remain inside it. In this sense, the particle is locked in a box. It may be in a region of space of length L, but nowhere else.
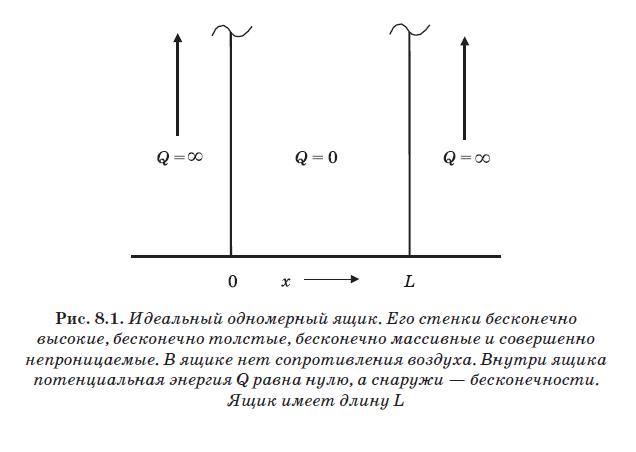
In fig. 8.2 depicts a racquetball ball bouncing off the walls of an ideal one-dimensional classic (large) racquetball court. As already mentioned, these walls are ideal, but inside there is no air resistance. In addition, the ball is also perfect, that is, it has absolute elasticity. When the ball collides with the wall, it shrinks like a spring, and again straightens, which causes it to rebound. Real balls are not perfectly elastic. When the ball shrinks on impact, not all of the energy expended in squeezing it goes into pushing away from the wall. Part of the energy expended in compressing the ball goes to heat it. However, here we will consider the ball perfectly elastic. When hitting the wall, all the kinetic energy of the ball, which causes its compression, is then spent on pushing the ball away from the wall. Therefore, the speed of the ball just before the collision with the wall is equal to the speed of its rebound after the collision.
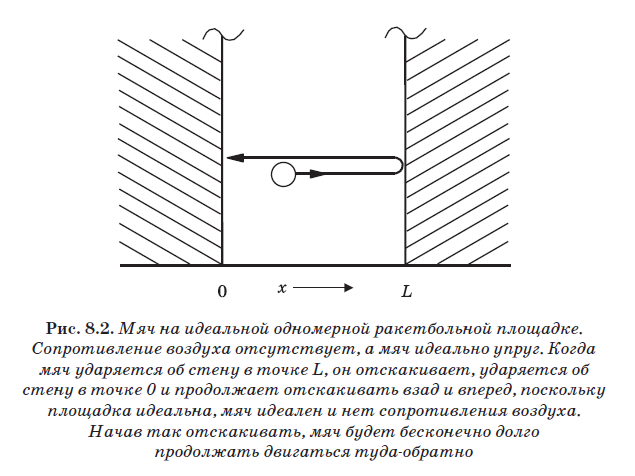
On this ideal rocketball platform, the ball bounces off the walls without any loss of energy; besides, there is neither air resistance nor gravity. Therefore, the ball will always move back and forth, reflecting from the walls. He will hit the wall at point L, bounce off, collide with the wall at point 0, bounce again and continue to move back and forth. Inside the box, since the potential is zero (see Figure 8.1), no forces act on the ball. Therefore, its energy is purely kinetic:
where m is the mass of the ball, and V is its speed. If the ball experiences weak external influences, its speed will become slightly less and the value of Ek will also decrease slightly. In this ideal rocketball, energy can change in a continuous fashion. The value of Ek can be increased or decreased arbitrarily depending only on the strength of the impact on the ball.
Another important feature of classic racball is the ability to stop the ball so that it lies motionless on the floor. In this situation, its speed is zero: V = 0. And once V = 0, then Ek = 0. At V = 0, the impulse is also zero, because p = mV, so we know the impulse exactly. If the ball lies on the floor (V = 0), then its position is known. If we mark this position x (see Fig. 8.2), then the value of x will be in the range from 0 to L. The value of x cannot take any other values, since the ball is on the court (in the box) and cannot be outside beyond the perfect walls. The ball can be placed in a certain position x on the floor of the court, and then its position will be known for sure. This is a property of a macroscopic playing field, even an ideal one. This is a classical system, and it is possible to accurately and simultaneously know the momentum p and the position x in it.
The racquetball court has a length of 12 m, the ball diameter is 5.6 cm, and its weight is about 0.04 kg. Obviously, the game of racquetball is described by classical mechanics. With the help of light, you can follow the ball bounce back and forth without affecting them.
A particle in a box - a quantum case
What will change if we now turn to the consideration of quantum racball? The site remains perfect, but now its length is not 12 m, but 1 nm (10–9 m). In addition, the particle has an electron mass of 9.1 10–31 kg, not 0.04 kg. Thus, this is a quantum particle problem in a box.
We can immediately say that the lowest energy of a quantum particle in a nanometer-sized box cannot be zero. On a classic rocketball platform, the ball's speed V, which is equal to zero, is possible, which means that the momentum p = mV can also be zero. In addition, the position of the ball x has a clearly defined meaning. For example, the ball may lie motionless (V = 0) exactly in the middle of the court, which corresponds to x = L / 2. In this case, for our classical rocket ball ∆p = 0 and ∆x = 0. The value of the product ∆x∆p = 0 does not correspond to the Heisenberg uncertainty principle, which is normal, since we are talking about a classical system. However, an absolutely small particle in a nanometer-sized box is a quantum object and must obey the uncertainty principle, which states that ∆x∆p ≥ h / 4. If V = 0 and x = L / 2, then we know both x and p, and therefore, ∆x∆p = 0, as in classical racquetball. For a quantum system this is not possible. Thus, V cannot be zero. A particle cannot remain motionless at a given point. And if the value of V is nonzero, then the value of Ek cannot be equal to zero. The uncertainty principle says that the least energy of our quantum rocket ball cannot be zero. A quantum ball never stays still.
Quantum particle energy in the box
What energy can a quantum particle have in a nanometer-sized box? This question can be answered without complicated calculations, but first we need to return to the waves again. In chapter 6 we talked about the wave functions of free particles. The wave function of a free particle with a certain momentum p is a wave that extends over the entire space. Thus, an electron with a perfectly defined momentum is a delocalized wave, spanning the entire space. The probability of finding a free electron is the same everywhere. Such an electron has a well-defined kinetic energy Ek = 1 / 2mV2, since it has a well-defined momentum p = mV.
An electron in a nanometer box is similar to our free particle as far as the inside of the box is concerned, where Q = 0. There is no potential inside the box, which means there are no forces acting on the particle. In this regard, it is very similar to a free particle, to which no forces act either. However, there is an important difference between a particle in a box and a free particle - these are the walls of the box. The electron in the box is only inside the box. The ideal character of the box does not allow its wave function to spread to the whole space. The particle is inside the box and can never be outside. The wave function sets the amplitude of the probability to detect a particle in a certain region of space. This is the Born interpretation of the wave function. If our electron can be detected only inside the box and never outside, then the probability of its detection in the box must be finite, and outside it must be zero. If the probability of finding a particle outside the box is zero, then the wave function must be zero at all points outside the box.
So, we came to the conclusion that the wave function of a particle in a box is similar to the wave function of a free particle, but the wave function must be zero outside the box. In his interpretation of the nature of the quantum-mechanical wave function, Born imposed some physical constraints on the form that the wave function can take. One of them is that a good wave function should be continuous. This condition means that the wave function should smoothly change from place to place. An infinitesimal change in position cannot lead to an unexpected jump in probability. This is a very simple idea. If the probability of detecting a particle in some very small region of space is, for example, 1%, then the displacement by an unimaginably small amount cannot suddenly make the probability of finding a particle equal to 50%. This is clear from the wave packet images in fig. 6.7. The probability of smoothly changing from place to place. This allows us to add something to the description of the wave functions of a particle in a box besides the fact that they are waves with finite amplitudes inside the box and zero amplitude outside. Since the wave function must be continuous, directly at the wall of the box from the inside it must have zero amplitude in order to coincide with the zero amplitude of the wave function outside the box.
In fig. 8.3 shows the (forbidden) discontinuity of the wave function inside the box. The wave function is indicated (Greek letter "phi"). The vertical axis represents the amplitude of the wave function. The dashed line shows its zero level. Wave functions, which are probability amplitude waves, can oscillate between positive and negative values. The wave function presented in fig. 8.3, has near the walls values other than 0. However, the wave function must be zero outside the box, that is, for values of x less than 0 and more than L, it must be zero. In the figure, the wave function unexpectedly jumps from a nonzero value at the wall inside the box to a zero value just behind the wall outside the box. Thus, the wave function shown in Fig. 8.3, is not valid because it is not continuous. This function cannot represent a quantum particle in a box.
The wave function should be zero at the walls.
In order for the wave functions representing the particle in the box to be physically acceptable, their values at the walls must be zero, and then they will not experience a break in the walls. To fulfill this condition is not difficult. The wave function oscillates between positive and negative values. Each time, moving from positive to negative or from negative to positive, it passes through zero. In fact, the zero points are separated from each other by half the wavelength. Therefore, to obtain good wave functions of a particle in a box, we must choose waves, the length of which allows them to fit in the box so that the zero points are located just on the walls.
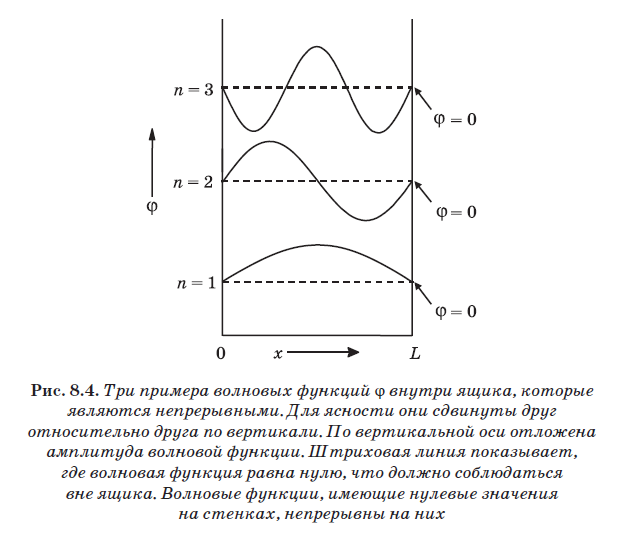
In fig. 8.4 shows three examples of waves that are suitable for the role of wave functions for a particle in a box. The lower one is n = 1 and consists of one half-wave. It starts on the left at an amplitude of 0, passes a maximum, and then descends again to zero on the wall at point L. The next wave, located above and denoted by n = 2, consists of one complete oscillation. It also starts at the left wall on amplitude 0, passes a positive peak, returns to zero, then a negative peak follows and returns to zero on the wall at point L. The wave, designated n = 3, contains one and a half periods. Any wave that contains an integer number of half-waves, that is, 1, 2, 3, 4, 5, and so on half of the wavelength, and is located so that it starts at zero on the left and ends at zero on the right, is appropriate.
The value of n is the number of half-waves of a specific wave function. When n = 1, the wavelength is 2L, since the length of the box is L, and n = 1 corresponds to half the wavelength. When n = 2, the wavelength is L, since exactly one wavelength is placed between the walls. When n = 3, three half-waves are placed between the walls, that is, 1.5 = L. In this case, = L / 1.5, that is, = 2L / 3. Note that a general rule is found here: = 2L / n, where n is an integer. For n = 1, we get = 2L, for n = 2 - = 2L / 2, for n = 3 - = 2L / 3, etc.
»More information about the book can be found on
the publisher's website.»
Table of Contents»
ExcerptFor readers of this blog 20% discount coupon -
Fire