Hello, my name is Alexander, and I am a physicist. From the side it may sound like a sentence, but in fact it is. It turned out that I am engaged in fundamental research in physics, namely, I investigate accelerated charged particles: protons and all those that are more positive ions, that is. In research, I do not use large accelerators like the LHC, but I shoot a laser at the foil, and a proton impulse takes off from the foil.

Now a few words about me. I graduated from the ITMO Faculty of Photonics and Optoinformatics in St. Petersburg, then went to magistracy at Aalto University (in Finland) in the direction of micro- and nanotechnology, and then spat on all these little things, microscopes, and especially on a clean room. And I went to fundamental science with big lasers. Now I am working in graduate school in the south-west of Sweden in the city of Lund in the university of the same name. This is about the distance of a cannon shot from Copenhagen.
As accelerated and flew
By themselves, charged particle accelerators are not a new idea, but the method by which I disperse them is relatively fresh, about my age. It allows you to significantly reduce the size of the accelerator and its cost, including the cost of work and maintenance. The difference between the two types can be estimated in the picture below.
 On the left - an electrostatic linear accelerator (slightly disassembled); On the right - my little, but proud doer of holes in foil
On the left - an electrostatic linear accelerator (slightly disassembled); On the right - my little, but proud doer of holes in foilLet's compare these two samples of the gloomy physical genius in more detail. Look at the left accelerator and the right, then again on the left and again on the right: yes, mine is on a horse (joke - author's note). In fact, mine takes only a meter in diameter, and the protons themselves are accelerated from a piece of foil. Her holder is located exactly in the middle of the circle, she is wearing a beautiful copper skirt. It is much simpler and more compact than the left sample, which is the size of a bus and, in addition, filled with suffocating gas. So, self-established enough (in physics it often happens that the less - the better), you can turn to the physics of the acceleration process.
Since we accelerate charged particles, it is most logical to do this with an electric field. The field we will be characterized by tension. For those who after school went to the front and back-end, let me remind you: the
electric field strength is a vector physical quantity characterizing the electric field at a given point and numerically equal to the ratio of the force acting on a fixed point charge placed at a given field point to the magnitude of this charge (dirty copy-paste from Wikipedia). It has dimension V / m. Returning to the comparison, the accelerator on the left accelerates protons to 4 MeV (Mega-electronvolt), that is, 2.77 * 10
7 m / s or 9.2% of the speed of light. Since the proton charge is 1, and the length of the accelerator is about two meters, the field strength will be 2 MV / m. Here we assumed that in all places the field was directed in one direction and, in general, was very close to the truth. A stylish accelerator has a field strength of the order of several TV / m, that is, about a million times more. Still, we must admit that its length is only a few microns.
So, at this point we found out whose field is steeper. It is time to turn to the physical and engineering mechanisms that this field creates. In the case of a conventional accelerator, there are two metal sheets, one of which is negatively charged, and the second in no way. Remember the school experiment about rubbing ebonite sticks with a piece of wool. Here the principle is the same, but the execution is much more complicated. If the protons are accelerated from the foil, then the field is created by electrons, the electrons fly out of the hot plasma, the plasma is obtained and heated by the laser, and all of this is the rest of the post.
Do you want me to knock him, and he will turn purple in speck?
If you hit hard enough, you can see a lot of wonderful physical phenomena. This is how the Harvard guys got metallic hydrogen, and then lost it.
In my case, I shoot a laser on the foil. I will describe it in more detail after explaining the non-trivial physics of the processes of obtaining warm dense matter, which is precisely how plasma is called scientifically, the culprit in the triumph of the acceleration of my protons. And now about everything in order.
The laser generates pulses with a wavelength of 800 nm and 35 fs with a duration (10
-15 s), that is, the actual pulse length in vacuum is approximately 10 μm. About 2 J of energy is pushed into this impulse, and that is a lot. If you take this impulse and focus on the foil into a neat round spot of 5 μm in diameter, the intensity will be about 10
20 W / cm
2 . This is indecent a lot. Again, a little bit of comparisons: you can safely cut steel at an intensity of 10
8 W / cm
2 (well, or so).
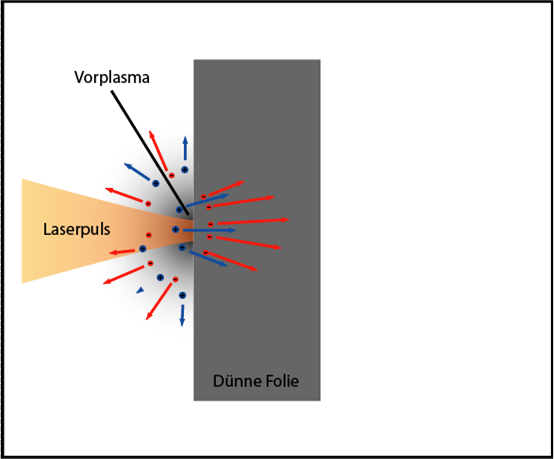
In fact, the laser pulse, due to the design features of the amplifier, has a preceding pedestal of about 500 ps in duration, and this very pedestal greatly helps accelerate protons well.
Ionized means armed
Recall what happens to light when it enters a substance. Energy should be saved, which means there are only three options for events: reflection, transmission and absorption. In the harsh life there are all listed at once. At a very early stage, we are interested in absorption.
So, we have a pedestal, which we also perfectly focus on a piece of foil, and there it is perfectly absorbed. In order not to go into the complexity of solid state physics, we consider the absorption of a single atom. From quantum mechanics, we know that only a photon can be absorbed, whose energy is exactly equal to the energy of an electron transfer from one state to another. If the photon energy is greater than the ionization energy (that is, sending an electron from the parent nest to a free trip), then the excess will turn into the kinetic energy of the electron, everything is simple. In our case, photons with a wavelength of 800 nm do not have enough energy (this is the energy of a single photon, and not the entire pulse!) To ionize a target, but here physics comes to our rescue. Remember, I mentioned a high radiation intensity? If in the appendage we still remember that light can be represented as a stream of photons, and its intensity is directly proportional to it, then it turns out that the flow of photons is very large. And if the flux is so large, then there is a high probability that several photons will fly to one place and at the same time, and if they absorb energy, they will develop, and ionization will still happen. This phenomenon, oddly enough, is called multiphoton ionization, and we regularly use it.
At the moment we have that the electrons have been successfully cut off, which means that the main impulse arrives at the ready-made plasma and begins to heat it.
Basics of plasma physics (did not come up with a joke, ah)
Before heating it is worth telling a little about the plasma as a state of matter. Plasma, it is like a gas, only electrons separately, and the nuclei separately. We will consider our plasma almost ideal gas, but consisting of electrons.
Our main characteristic of the plasma will be its density (the number of electrons per unit volume), we will denote this value as $ n_e $ (not to be confused with the refractive index!), And the temperature of these electrons themselves, that is, their average velocity. This is described by the Boltzmann distribution in the same way as in the school physics course:
$$ display $$ \ frac {m_e v ^ 2} {2} = \ frac {1} {2} k_B T_e, $$ display $$
where it is easy to follow
$$ display $$ \ langle v \ rangle = \ sqrt [] {k_B T_e / m_e}, $$ display $$
Where
$ inline $ k_B $ inline $ - Boltzmann constant,
$ inline $ t_e $ inline $ - electron temperature, well, and
$ inline $ m_e $ inline $ - electron mass. Yes, here we have considered the one-dimensional case, but we don’t need more to describe our processes, in fact.
Now we will apply an electric field to the plasma already described. Let me remind you that the plasma consists of charged particles, which means that at a given density at some distance from the place where we applied the field, the electrons will shield (shield) the source (such a crowd of small Matrosovs - author's note). The distance that is necessary for this is called the Debye length and is given by the equation
$$ display $$ \ lambda_D = \ sqrt [] {\ frac {\ epsilon_0 k_B T_e} {q ^ 2_e n_e}}. $$ display $$
Here
$ inline $ q_e $ inline $ obviously the electron charge as well
$ inline $ \ epsilon_0 $ inline $ - dielectric constant of vacuum, such a fundamental constant. Let's analyze this formula a little to see simple process physics behind it. Increasing the density of electrons, we reduce the average distance between them, as a result, for a shorter distance we collect enough electrons to completely shield our field. On the other hand, the greater the temperature, the greater the average distance between the electrons.
Due to the screening effect and the quite definite (from the temperature) average electron velocity, the plasma responds to the field that has suddenly flown not instantaneously. It is logical to assume that the response time is associated with the Debye length and velocity of the electrons. A good analogy is throwing a stone into a lake. In comparison with the whole lake, the stone acts on the surface of the water pointwise. Part of the water changes immediately (this is where it splashed), and then the waves begin to spread along the water surface. In the case of a plasma, the electric field that suddenly appeared is a stone. The size of the plume is determined by the screening length (the field does not act further than it), and the wave propagation depends on how close the electrons are to each other. We can introduce such a characteristic as plasma response time:
$ inline $ t_D = \ lambda_D / v $ inline $ . By and large, it shows us the time in which information about a change in the applied field will reach those electrons that, as it were, have not seen this field.
Since we are physicists, we don’t really like time. It is much more convenient to work with frequencies, so we introduce the concept of plasma natural frequency. This value will show us how often we can change the field so that all the electrons that we proudly call a plasma have time to react to these changes. Well, what could be easier? Let's divide the unit by the response time, and here it is - the frequency:
$$ display $$ \ omega_p = \ frac {1} {t_D} = \ sqrt [] {\ frac {q ^ 2_e n_e} {\ epsilon_0 m_e}}. $$ display $$
It is easy to see that the natural frequency of plasma oscillations depends on the electron density. The more electrons, the greater the frequency. You can draw another analogy, but this time with a spring pendulum. The high density of electrons tells us that they are closer to each other, and therefore they interact more strongly. Suppose that their interaction is directly proportional to the elasticity of the spring of the pendulum. And the greater the elasticity, the higher the oscillation frequency.
The natural frequency of the plasma also determines its refractive index. If you honestly write the wave equation for the collective motion of electrons in a plasma, and then assume small changes in the electron density (we will not do this here, because it’s boring), then the refractive index is set like this:
$$ display $$ \ eta = \ sqrt [] {1- \ frac {\ omega ^ 2_p} {\ omega ^ 2_0}}. $$ display $$
Here
$ inline $ \ omega_0 $ inline $ - circular frequency of the applied electric field. She is glad / s and not in Hz!
Let's look closely at this expression. As an experimental physicist, I don’t drink souls in real numbers, but I try to ignore complex ones, especially the complex index of refraction. Well, how can light, in the end, propagate in a substance
i times slower than in a vacuum? This is some kind of nonsense! Actually not, but more on that another time. If a
$ inline $ \ omega_0> \ omega_p $ inline $ , the expression has a real value, and the alternating electric field propagates inside our plasma. Everyone is happy, and we will not magnify such a plasma sufficiently dense. However if
$ inline $ \ omega_0 <\ omega_p $ inline $ , then the refractive index becomes not only complex, but entirely imaginary. In this case (and not just because I wanted to) the wave will not propagate there at all, but will immediately reflect without loss. This is too dense plasma. Very cool phenomenon, by the way. It is called a plasma mirror.
And as a dessert
$ inline $ \ omega_0 = \ omega_p $ inline $ . This is a plasma of critical density. In this case, it begins to resonate with a forcing (given by us) alternating electric field. For such a special case, you can even enter the concept of critical density and set it like this:
$$ display $$ n_c = \ frac {\ epsilon_0 m_e \ omega ^ 2_0} {q ^ 2_e}. $$ display $$
Naturally, for each frequency of the driving field, the critical density is different.
SHOCK! Heating the plasma! For this you need only ...
In our case, we will focus on only one heating mechanism that prevails in the experiment.
To begin with, let the plasma that we formed by the pedestal will have a smooth density gradient, in this case we have heating through resonance absorption. An illustration of this in the image below.
 Illustration of the process of resonance absorption: a) the distribution of the density of electrons near the front side of the target; b) refraction of a laser beam in a plasma with a density gradient; c) plasma electric field
Illustration of the process of resonance absorption: a) the distribution of the density of electrons near the front side of the target; b) refraction of a laser beam in a plasma with a density gradient; c) plasma electric fieldSo, the laser shines at our plasma at an angle, well, let it be 45 degrees, and at the same time it is polarized in the plane of incidence. Polarization is indicated by the red arrows in the figure. Our plasma has a density gradient, which means its refractive index changes continuously (here it grows). At some point, it will happen that a plasma layer for our laser will become “turning” and it will be reflected, that is, for some time it will spread parallel to the critical layer. It is important to note that it will turn before it reaches the layer with critical density, since we launched it at an angle to the normal. The density of the plasma at which the laser beam will turn is given by the equation:
$$ display $$ n_t = n_c \ cos ^ 2 \ alpha, $$ display $$
Where
$ inline $ n_c $ inline $ - critical density, and
$ inline $ \ alpha $ inline $ - the angle of incidence of light.
Now the fun begins. Recall that light is not only a photon flux, but also an electromagnetic wave, that is, our pulse has an electric field that oscillates harmonically with a large amplitude. When light propagates parallel to the critical layer, a standing wave is formed, which does not change over time (naturally, while the laser pulse is in place). The field of this wave, in fact, penetrates beyond the plasma layer where the light has turned, and reaches the critical layer. Let me remind you that the frequency of plasma oscillations in the critical layer is the same as the frequency of laser radiation, which means resonance occurs. When the laser ceased to shine, the energy that it transmitted to the electrons in the critical layer is distributed through the blows to the other electrons, and this means that the plasma is heated.
So where is the acceleration?
Now, when we are well heated electrons in the plasma, and the laser no longer shines, you can tell how the protons are accelerated. To do this, look at the pictures below. Up to this point I did not say where the protons come from. Naturally, they do not appear from the cores of the foil material. Since we are not very neat and do not wear gloves (hands are sweating heavily in them), water and hydrocarbons are on the surface of the foil. Ionized hydrogen is our invaluable source of protons. Checked: if you remove the pollution, then there will be no protons.
 | Plasma formation pedestal, that is, ionization of the front side of the target. As the target is usually used foil with a thickness of 0.4 - 12 microns. |
 | Here the main part of the pulse interacts with the created plasma and heats it. Some electrons are so well warmed that they fly out from the back of the target. |
 | When the electrons fly off quite a lot, the remaining positive charge in the foil pulls them back. In the plasma, they heat up again and fly out. For some time, a dynamic equilibrium is established. The electric field is directed perpendicular to the target. |
 | This very electric field separates protons and other ions (depending on what was there at all) from the back surface of the target, and then accelerates them. By the time the ions have accelerated, the electron cloud is already falling apart, and all the particles begin to fly farther together. And then we begin to believe that they do not interact anymore. |
Divide and rule
At the moment, the position is as follows: the laser does not shine for a long time, a hole in the foil, protons with electrons fly together from the target normally to its back surface. We don’t need electrons at all, that's why a magnet comes to the rescue. When a beam of charged particles flies through a magnetic field, the Lorentz forces deflect each particle in proportion to its speed and charge. Accordingly, protons and electrons will deviate in different directions, and we will not simply look towards electrons. By the way, the greater the proton energy (that is, its speed), the less it will deviate. This means that by setting the screen, which is sensitive to protons, we can see the energies of accelerated protons. A few more comparisons in figures: the magnet, which is permanent with us and creates a field of about 0.75 T; in MRI devices the magnetic field is 1.5 - 3 T.
In addition, we can see the profile of a beam of flying protons. He's round, by the way. And if we can also measure the energy of protons in each part of the beam, we will be able to unambiguously restore the shape of the electron cloud, which has accelerated our protons.
Instead of conclusion
It may be a fair question why all this is necessary. My favorite answer is just like that. This is a fundamental science, and trying to find her momentary use is meaningless. Perhaps in some years it will find its use in the treatment of cancer or thermonuclear fusion, but for now the main task is to learn something new about the world around us, just like that, because it’s interesting.
For particularly curious about the laser itself and its device
As promised, here I will talk about the laser, with which I do science. I have already mentioned some of the characteristics of our laser, but did not speak about the pulse repetition frequency. It is approximately 80 MHz. This frequency is determined only by the length of the resonator and is inverse to the time in which the light has time to fly around the resonator back and forth. Looking ahead, I will say that at such a frequency it is impractical to amplify impulses, it is incredibly difficult from an engineering point of view, and you cannot get enough electricity.
Especially to go into the laser theory, I will not. The basics of where laser radiation comes from are perfectly stated in a Wikipedia article on stimulated radiation. If you try to be very brief, then three components are necessary for laser radiation: the active medium (photons just fly out of it), the pumping (it maintains the active medium in a state in which there are more excited atoms that can radiate), and a resonator ( it ensures that photons copy each other during multiple passages through the active medium). If you put all the components together and pray, the laser will begin to shine, but continuously. If you try again, you can make it generate pulses, including such short ones as in my installation. For the most inquisitive, the method of generating femtosecond pulses is called passive mode locking. And now a small feature of very short pulses. It is often believed that the laser shines at the same wavelength, and in continuous mode, as well as on long pulses, it can even be called true. In fact, due to a number of complex physical processes, which we will certainly not discuss here, the temporal form of the pulse and its spectrum are connected by the Fourier transform. That is, the shorter the pulse, the wider its spectrum.
Suppose that we started the master oscillator, but the energy of its pulses is a few nJ. Remember, in the beginning I said that the energy in an impulse that arrives at a target is about 2 J? So, it is a billion times more. This means that the momentum needs to be strengthened, and we'll talk about it in more detail.
Short pulses are generally characterized by very large peak powers (remember, energy divided by time?), And this has a number of complications. If the light is shined on the medium with high intensity (power per unit area), then it will burn, and if the active medium is burned out, then nothing will be strengthened. That is why we choose a repetition rate of 10 Hz and amplify only them. Since there is a lot of equipment and it all works at such a frequency, we have a special box that distributes these 10 Hz to the whole hardware, and for each device you can choose a delay in receiving the signal with an accuracy of several picoseconds.
You can fight with high intensity in two ways. As it is easy to guess from its definition, you need to either increase the area or reduce power. With the first, everything is very clear, but the second method was the breakthrough of laser technology in the twentieth century. If the pulse is initially very short, it can be stretched, strengthened, and then squeezed again.
To understand how to do this, turn to the basics of optics. For different wavelengths, the refractive indices in the medium are different, which means (by the definition of the refractive index, by the way) that as the refractive index increases, the speed of light propagation in the medium decreases. And here we launched our impulse on Wednesday, and its red part passed the material faster than the blue one, that is, the impulse became longer, and its peak power dropped. Hooray, now nothing is burning! For deeper knowledge in this area, I recommend to google and read about amplifying chirped pulses (also known as Chirped Pulse Amplification or CPA).
All that is left for us to do is to increase the momentum, squeeze, focus and send it to make a hole in the foil!
And now some pictures with captions.
 Actually fotochka laboratory. Cylindrical crap in the middle is a vacuum chamber, because protons fly very lousy in the air and all the time they knock on its molecules. Well, in general, with a vacuum, everything looks better. The blue thing on the right is the lead wall, so as not to accidentally get superpowers and radiation sickness. The laser itself is behind the door, which is to the left with a yellow Achtung sign.
Actually fotochka laboratory. Cylindrical crap in the middle is a vacuum chamber, because protons fly very lousy in the air and all the time they knock on its molecules. Well, in general, with a vacuum, everything looks better. The blue thing on the right is the lead wall, so as not to accidentally get superpowers and radiation sickness. The laser itself is behind the door, which is to the left with a yellow Achtung sign. And here is the wall itself in profile. Yes, inside it is packed with lead, like Winnie the Pooh.
And here is the wall itself in profile. Yes, inside it is packed with lead, like Winnie the Pooh. Behind the wall is our command post, when we shoot, then safety is supposed to sit behind it. From radiation, we, of course, will not die, but you can easily go blind. There are five monitors on two computers, it is very easy to get confused in all this junk. , , . , .
Behind the wall is our command post, when we shoot, then safety is supposed to sit behind it. From radiation, we, of course, will not die, but you can easily go blind. There are five monitors on two computers, it is very easy to get confused in all this junk. , , . , . -. .
-. . . , . ( 1000 ) . , .
. , . ( 1000 ) . , . , . — — . , : . . . ( ) , , , . - .
, . — — . , : . . . ( ) , , , . - . , 15 . , — . , -190 .
, 15 . , — . , -190 . , . , 0,1\%. - , 160 . 960 , , . 10 . 80 , 8 .
, . , 0,1\%. - , 160 . 960 , , . 10 . 80 , 8 .Thanks for attention!