How the Higgs field works:- main idea
- Why the Higgs field is nonzero on average
- How does the Higgs particle appear
- Why the Higgs Field is Necessary
In the
previous article, I described how and why the Higgs field has a non-zero mean value. Now I want to describe what the Higgs particle is and how its mass arises from the equations.
I want to remind you that if the opposite is not mentioned, I always describe the simplest possible form of the field and the Higgs particle - the so-called "Higgs Standard Model." More complex forms are possible; for example, there may be several Higgs fields at the same time, instead of one. Perhaps I will describe a more complicated case in one of the following articles.
 Fig. 1: Class 1 field fluctuates in time around a stable value Z (x, t) = 0
Fig. 1: Class 1 field fluctuates in time around a stable value Z (x, t) = 0In the last article I did not emphasize this fact, but among the elementary fields discovered by us in nature, the Higgs field is unique. All fields except the Higgs satisfy the equations of motion of class 0 or 1. In fact (although this is probably not the case for all fields in nature), all fields known to us that satisfy equations of class 1 do this because the Higgs field is nonzero . If it were zero, they would all satisfy the equations of class 0 (as I explained in the first article). Instead, the Higgs field satisfies an equation that can be called an equation of class -1.
For the field Z (x, t), the classes I defined look like this:
The equations imply that B
2 > 0.
 Fig. 2: The field of class -1 leaves the unstable equilibrium Z (x, t) = 0.
Fig. 2: The field of class -1 leaves the unstable equilibrium Z (x, t) = 0.The minus sign between class 1 and class -1 is very important. In both cases, the solutions of the equations contain Z (x, t) = 0 as one of the special cases, but in class 1 Z (x, t) = 0 is stable, that is, Z (x, t) can fluctuate around zero; these are decently behaved waves with a massive quantum. And vice versa, for class -1, Z (x, t) = 0 is unstable, that is, Z (x, t) will not oscillate, but grow to larger and larger values. If you do not change the equation, the magnitude of the field will fly to infinity. More precisely, if the solution of the equation of class 1 is the oscillation Z, as in Fig. 1, solving the equation of class -1 will be an exponential growth of Z, as in Fig. 2
For the Higgs field, as well as for any field that exists in nature, the equation of class -1 is changed with the help of terms that limit exponential growth and prevent the field from going to infinity. As we saw in the previous article, the Higgs field obeys the equation of motion
It belongs to the -1 class when H is almost zero, but it has an important member of H
3 . Here b is a positive number, and v is the equilibrium position for H. This equation ensures that if the H field starts at the point H = 0 and moves from the unstable equilibrium position to a positive H, then it will oscillate around the stable equilibrium position in H = v (Fig. 3).
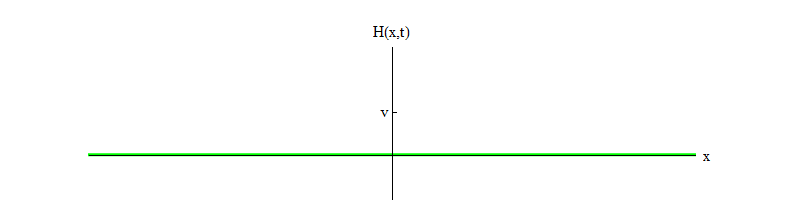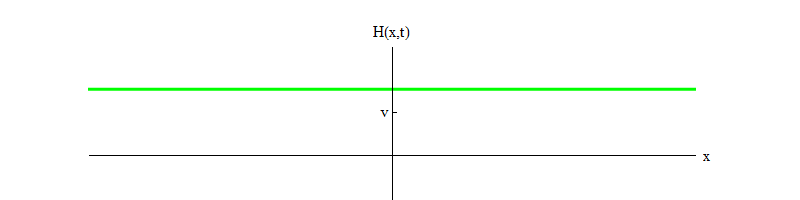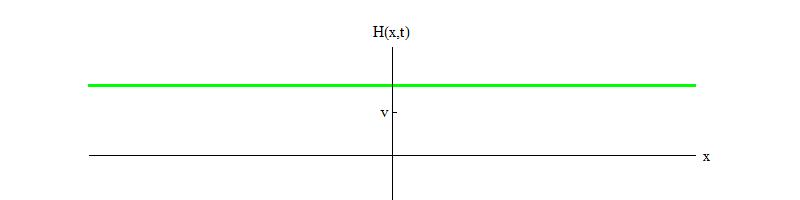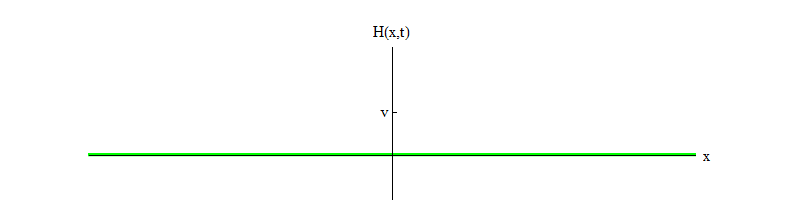 Fig. 3
Fig. 3Over time, the oscillations will subside, due to the terms of the equation of motion, which I omitted for brevity; they allow part of the oscillation energy of the field H to be transmitted to waves of other fields (these are the same nonlinear terms that
allow the Higgs particles to decay ). In time (Fig. 4), the H field will calm down in the position H = v.
 Fig. four
Fig. fourIf a physical process knocks a field from the position H = v in a small region of space, the field will emit waves of the form
Where A is the wave amplitude, ν and λ is its frequency and wavelength, and the relationship between ν and λ depends on the exact form of the equation of motion, in particular, on b and v. And the quanta of these waves will be Higgs particles. The million question: what is the mass of the Higgs particle? To calculate this, we need, as is always required for particles (representing wave quanta in relativistic fields), determine the relationship between the frequency ν and the wavelength λ of the waves of the corresponding field, and then multiply the result by Planck’s constant h to get the ratio between the energy and the quantum pulse of these waves, which will tell us the mass of the quantum (ie, particles).
We do this with the field S (x, t) mentioned in the
first article . We write a shifted version of the Higgs field, expressing it as H (x, t) = v +
h (x, t) , and substitute this into the equation of motion of the field H.
h (x, t) I will write bold to distinguish it from Planck's constant h. In the example for the field S, given in the review article, a simple equation of motion is indicated, so the shift did not change the mass of the particle S. But in this case it is not so! The equation of motion for the Higgs field is more complex, so the equation for h is very different from the original equation for H:
Where I used the fact that v is a constant and does not depend on space and time. Then we recall that the Higgs field quantum has a small amplitude, so when we study a single Higgs particle (that’s what we need to determine its mass), we can drop all terms proportional to h
2 and h
3 :
Where “+ ...” is reminiscent of dropped members. Note that this equation for h (x, t) belongs to class 1, although we started with an equation of class -1 for H (x, t); this is because H (x, t) was unstable in the region H = 0, and
h (x, t) is stable in the region
h = 0, where H = v. So we can calculate the mass m
h of the Higgs particle
h using the following equation of class 1:
h in the right side denotes the Planck constant. If a particle similar to the Higgs that was recently found at the LHC really turns out to be a Higgs particle of the Standard Model, then for the first time we will be able to find out what b is (remember that we already knew v a long time ago) and finally we can find out the value a = b v.
- v = 246 GeV;
- m h ≈ 125 GeV / c² (if the new particle is Higgs)
- b ≈ 0.35 (2 π / h) (if the new particle is the Higgs Standard Model)
- a = bv ≈ 87 GeV (2 π / h) (if the new particle is the Higgs Standard Model)
where h, again, is Planck's constant. And the last three quantities were not known to us until the recent discovery of the Higgs particle.
Now, if it turns out that the Standard Model does not correspond to nature (if it is necessary to add additional fields to the known fields besides H (x, t), to explain the properties of the recently discovered particle of 125 GeV / c²), let us assume that this particle turns out to be one of several types of Higgs particles - then we will have to deal with this difficult situation at the LHC for a few more years. One can imagine many possibilities, and it makes no sense to explain all of them to you, but roughly I described some of them here; and if the data obtained at the LHC show us a certain direction, I will definitely explain everything to you in detail.