 Single-shot shooting reminds us that photographs are photographs taken at a specific location at a specific time, and each moment is different from the previous one.
Single-shot shooting reminds us that photographs are photographs taken at a specific location at a specific time, and each moment is different from the previous one.When we imagine ways to move around the Universe, we immediately recall three dimensions. Right-left, forward-backward and up-down: three independent directions of Cartesian grids. All of them are considered dimensions - spatial. But we often talk about one more dimension, another type: temporary. But what does time measure? This week the reader will ask the following question:
I have always been amazed at the continuum consisting of 3 + 1 dimensions, space and time. Why do they always write about three spatial dimensions and one temporal dimension?
Let's start with the study of the three dimensions of space known to us.
 On the surface of the Earth, two coordinates, latitude and longitude, are sufficient to determine the position
On the surface of the Earth, two coordinates, latitude and longitude, are sufficient to determine the positionOn the surface of the Earth, we usually need two coordinates to determine the location: latitude and longitude, or the position along the axes from north to south and from west to east. If you want to go down to the ground or rise above the surface, to describe your position you will need a third coordinate - height / depth, or your position along the vertical axis. After all, if someone is exactly in the same place as you, in terms of latitude and longitude, but at the same time it is located in a tunnel under the ground or in a helicopter over your head - one cannot say that it is in the same place as you. To describe your location in space, three independent pieces of information are required.
 Your position in the Universe is described not only by spatial coordinates (where), but also temporal (when)
Your position in the Universe is described not only by spatial coordinates (where), but also temporal (when)But space-time is more complicated than just space. The position of the chair on which you are sitting now can be described by three coordinates - x, y and z. But now you are sitting on it, and an hour ago, yesterday, or ten years ago, this could not be so. To describe an event, the knowledge where it takes place is not enough; besides, you need to know when, that is, you need a time coordinate, t. For the first time it played a large role in the theory of relativity, when we talked about the problem of simultaneity. Imagine two different places connected by a path that two people walk, each from their place, to another.
 Two points connected by one-dimensional linear path
Two points connected by one-dimensional linear pathTheir trip can be imagined by placing two fingers from different hands on the two starting points, and having them move towards the goal. At some point they will have to go past each other, that is, your fingers will be in the same place at the same time. In relativity, this is known as a simultaneous event, and it can occur only if all the spatial components and all the temporal components of two different physical objects coincide.
There is nothing contradictory in this, and this explains why we need to treat time as a dimension in which we move, just like any of the spatial dimensions. But it was Einstein’s technical service station that prompted his former professor
Hermann Minkowski to develop a theory combining three spatial and one time dimensions.
 Whether space is flat or curved, movement in space affects movement in time.
Whether space is flat or curved, movement in space affects movement in time.We understand that to move in space you need to move in time; if at the moment you are here, you cannot be in another place at the same time - you can only get there later. In 1905, the Einstein service station taught us that the speed of light is the universal limit of speed; as you approach it, you begin to experience strange phenomena of time dilation and distance shortening. But the biggest breakthrough came in 1907, when Minkowski realized that Einstein’s relativity produced an amazing conclusion: from a mathematical point of view, time behaves like space, except for c, the speed of light in a vacuum, and i, an imaginary unit √ ( -one).
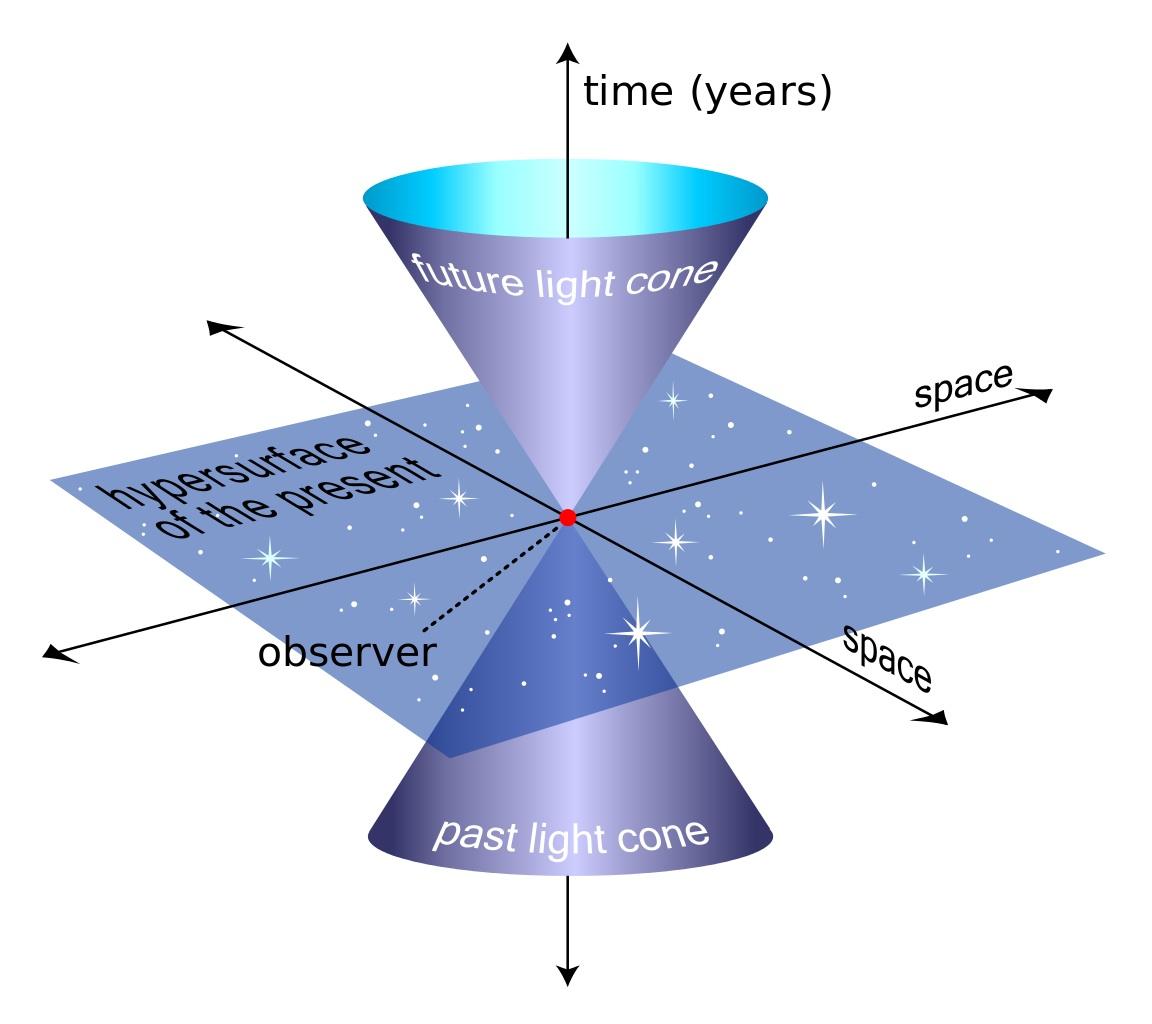 An example of a light cone, a three-dimensional surface of all possible light rays arriving at a point of space-time and emanating from it
An example of a light cone, a three-dimensional surface of all possible light rays arriving at a point of space-time and emanating from itIf you put all these discoveries together, you will get a new picture of the Universe related to our movement within it:
• If you do not move and remain in the same place in space, you move in time with maximum speed.
• The faster you move in space, the slower you move in time, and the shorter the spatial distances you see in your direction of motion.
• If you have no mass, you can only move at the speed of light, instantaneously moving in the direction of your movement, without any passage of time. [more precisely, from the point of view of a massless particle, it does not move and time does not move - approx. transl.]
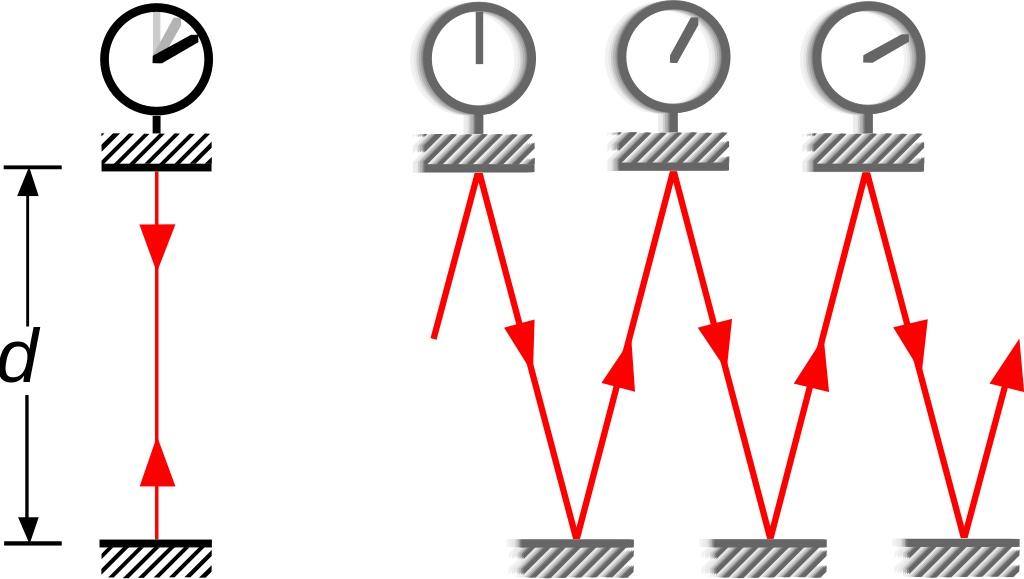 For a stationary observer, time is normal, and for a clock moving fast in space, the clock is slower than that of a stationary
For a stationary observer, time is normal, and for a clock moving fast in space, the clock is slower than that of a stationaryFrom a physical point of view, the consequences are striking. This means that stability is inherent in all massless particles, since for them there is no flow of time. This means that unstable particles, like a muon, created in the upper atmosphere, can reach the Earth’s surface, despite multiplying their lifetime (2.2 μs) by the speed of light, we get a distance of 660 meters, which is much less the path that they need to take. And this means that if you take a pair of identical twins, leave one on Earth, and send the other on a relativistic journey into space, the second twin will return to be younger than the first, since it will take less time for it.
 Mark and Scott Kelly at the Johnson Space Center. One of them spent a year in space and aged a little less, while the other remained on Earth.
Mark and Scott Kelly at the Johnson Space Center. One of them spent a year in space and aged a little less, while the other remained on Earth.As Minkowski wrote in 1908:
Theories about the essence of space and time, which I want to demonstrate to you, have grown on the basis of experimental physics, from which their strength comes. They are radical. Henceforth, space itself and time itself are doomed to turn in the shadows, and only their union will remain an independent reality.
Today, the formulation of space-time is even more general, the curvature inherent in space is included in it, as STO is generalized. But the reason that time is the same dimension as space is that we constantly move through it, and write it in the form of “3 + 1” (and not just 4) because an increase in movement through space reduces movement through time and vice versa.
 The camera predicts the movement of an object in time - one of the practical applications of the idea of time as a measurement
The camera predicts the movement of an object in time - one of the practical applications of the idea of time as a measurementIt is interesting that everyone, regardless of their movement through space in relation to everyone else, will see the same rules, the same actions and consequences. If time were not such a measurement, the laws of relativity would not work, and the concept of absolute space could be justified. For physics to work the way it works, we need time to have the property of measurement, and the Universe continually provides us with similar phenomena.
Ethan Siegel - astrophysicist, popularizer of science, blog Starts With A Bang! He wrote the books Beyond The Galaxy , and Treknologiya: Star Trek Science [ Treknology ].