
"Theoretical minimum" - a book for those who missed the lessons of physics in school and college, but already regret it. Want to understand the basics of the natural sciences and learn how to think and reason like modern physicists do? In original and non-standard form, famous American scientists Leonard Susskind and George Grabowski offer an introductory course in mathematics and physics for inquiring minds.
Unlike other popular science books, trying to explain the laws of physics in an accessible way, deftly evading equations and formulas, the authors teach the reader the classical basics of the natural sciences. The book offers its own original teaching methodology, supplemented by video lectures published on the site
theoreticalminimum.com .
Lecture 9. Phase fluid and the Gibbs – Liouville theorem
Lenny liked to look at the river, especially to watch the small specks floating on the surface. He tried to imagine how they would move between stones or getting into whirlpools. But the flow of the river as a whole — the cumulative movement of a large volume of water, with separating, converging and overtaking streams — was beyond its comprehension.
Phase liquidTo concentrate on specific initial conditions and to follow a separate trajectory in the phase space is very natural for classical mechanics. But there is a broader view that encompasses a whole family of trajectories. Instead of placing the tip of a pencil at some point in the phase space and tracing a single trajectory from there, try to do something more ambitious. Imagine that we have an infinite number of pencils, and use them so that we uniformly fill the phase space with dots (by homogeneity, I mean that the density of points in q, p is the same everywhere). Consider these points as particles that make up an imaginary fluid filling the phase space.
Let now each point move according to the Hamiltonian equations of motion:

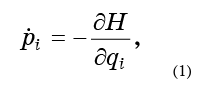
so that our fluid flows endlessly in phase space.
The harmonic oscillator is a good initial example. In lecture 8, we saw that each point moves in a circular orbit with a constant angular velocity. (Let me remind you that we are talking about phase, not about coordinate space. In a coordinate oscillator, it moves back and forth in one dimension.) The entire fluid makes a solid-state motion, rotating uniformly around the origin of the phase space.
Now back to the general case. If the number of coordinates is N, then the phase space and the liquid in it are 2N-dimensional. The fluid flows, but in a very specific way. Her flow has special properties. One of them is that if a point starts with a certain energy - that is, for a given value of H (q, p) - then it saves this value of energy. Surfaces of constant energy (for example, with an energy equal to E) are determined by the equation H (q, p) = E. (2)
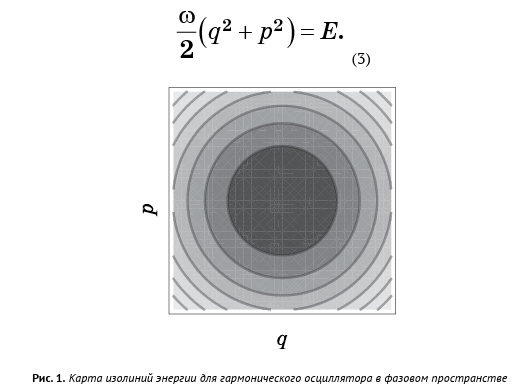
For each value of E, we have one equation with 2N variables of the phase space, which defines a surface of dimension 2N - 1. In other words, for each value of E there is its own surface; when you go over all values of E, these surfaces fill the entire phase space. It is possible to consider the phase space with the surfaces given by equation (2) as a map of isolines (Fig. 1), on which the horizontal lines represent not the height, but the energy values. If a fluid point is on a certain surface, it will remain on it forever. This is the law of conservation of energy.
The phase space of the harmonic oscillator is two-dimensional, and the energy surfaces are circles:
In the general case, the energy surfaces of a mechanical system are too complex for visualization, but the principle remains the same:
energy surfaces fill the phase space as layers, and the flow moves so that the points remain on the surface on which they were originally .
Short reminderHere I would like to stop and recall what was mentioned in the very first lecture, where coins, bones and the simplest ideas about the laws of motion were discussed. We described these laws with a set of arrows connecting points that represent the states of the system. We also explained that laws are permissible and invalid, and permissible are reversible. The point is that each point must have exactly one incoming arrow and exactly one outgoing. If at least at one point the number of incoming arrows exceeds the number of outgoing (this is called convergence), then such a law is irreversible. The same applies to the case when there are more outgoing arrows than incoming arrows (this is called divergence). Both divergence and convergence of shooters violate reversibility and are prohibited. So far we have not returned to this line of reasoning. Now the time has come.
Flow and divergenceConsider some simple examples of fluid flow in ordinary space. Let's forget about the phase space for a while and just consider the usual fluid moving in the usual three-dimensional space with the axes designated as x, y, z. The flow can be described by
the velocity field . Velocity field
is determined by setting the velocity vector at each point in space (Fig. 2).
You can also describe the velocity field by the velocity components:
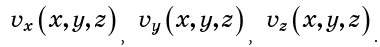
Also, the speed at a point may depend on time, but let's assume that this dependence does not exist. In this case, the flow is called
stationary .
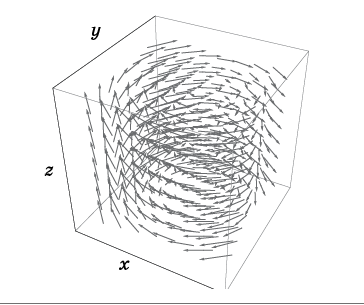
Fig. 2. Speed field
occupies the same volume. It also means that the density of a liquid — the number of molecules per unit volume — is the same everywhere and unchanged in time. By the way, the term "incompressibility" also means inextensibility. In other words, the liquid can not increase in volume. Consider a small cubic cell, given the conditions:
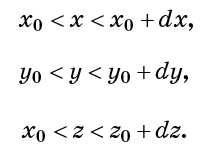
Incompressibility implies that the number of fluid points in each such cell is constant. It also means that the total fluid flow entering the cell (per unit time) must be zero. (The number of points in the flow enters, the same goes out.) Consider the number of molecules passing per unit time through the cell surface x = x0. It will be proportional to the flow velocity on this surface vx (x0).
If the velocity vx is the same at x0 and at x0 + dx, then the flow into the cell through x = x0 will be the same as the flow from it through x = x0 + dx. But if vx changes throughout the cell, then these two streams will be unbalanced. The total flow going to the cell through these two faces will be proportional to
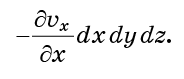
Exactly the same reasoning applies to the faces y0 and y0 + dy, as well as z0 and z0 + dz. If all of them are folded, then the total flow of molecules inside the cell (inflow minus outflow) will be
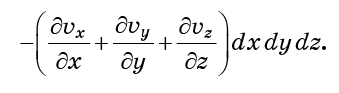
The combination of derivatives in brackets is called the divergence of a vector field
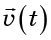
and denoted by
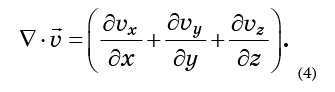
Divergence reflects the degree of scattering of molecules, or the increase in the volume they occupy. If the fluid is incompressible, this volume should not change, which means that the divergence must be equal to zero.
One way to understand incompressibility is to think of each molecule or point as occupying a volume that cannot be changed. They can not be compressed into a smaller volume, they do not disappear and do not appear from nowhere. A little thought, you can see how similar the incompressibility and reversibility. In the examples that we discussed in lecture 1, the arrows also defined a kind of flow. And in fact, this stream was incompressible, at least if it was reversible. A natural question which follows from this: is the flow in the phase space reversible? The answer is yes, if the system satisfies the Hamilton equations. And the theorem expressing this incompressibility is called the Liouville theorem.
Liouville theoremLet us return to the flow of fluid in the phase space and consider the components of the velocity of the fluid at each point of the phase space. Needless to say, the phase fluid is not three-dimensional in x, y, z coordinates. It is a 2N-dimensional fluid in the coordinates pi, qi.
Thus, there are 2N components of the velocity field — one for each q coordinate and each p coordinate. Denote them

The concept of divergence, expressed by equation (4), is easily generalized to any number of dimensions. In three dimensions, this is the sum of the derivatives of the velocity components in the corresponding directions. Similarly, it is defined for any number of measurements. In the case of phase space, the divergence of flow is the sum of 2N members:
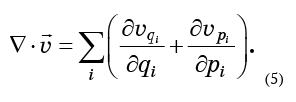
If the fluid is incompressible, then this expression must be zero. To calculate it, one needs to know the components of the velocity field — they, of course, are nothing but the velocities of the particles of the phase fluid.
The flow vector at a given point is identified with the speed of an imaginary particle at that point. In other words,
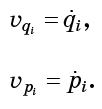
And

- these are just the quantities that are included in the Hamilton equations (1):
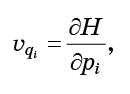

All you need to do is to substitute the equations (6) into the formula (5) and get
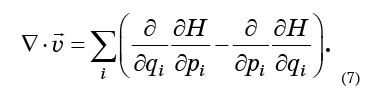
Recalling that the second derivative of the form
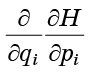
does not depend on the order of differentiation, we understand that the terms of equation (7) in pairs exactly destroy each other:
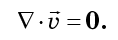
So, the phase liquid is incompressible. In classical mechanics, the incompressibility of a phase fluid is called the Liouville theorem, although it has almost nothing to do with the French mathematician Joseph Liouville. The first in 1903 was published by the great American physicist Josiah Willard Gibbs, and it is also known as the Gibbs – Liouville theorem.
We determined the incompressibility of the fluid, demanding that the total amount of fluid entering any small cell be zero. There is another strictly equivalent definition. Imagine the volume of fluid at some point in time. This volume can be of any shape: spherical, cubic, drop-shaped - any kind. Now trace the movement of all points of this volume. After some time, a drop of liquid will be in another place and have a different shape. But if the fluid is incompressible, the drop volume will remain the same as it was originally. So we can reformulate the Liouville theorem: the
volume occupied by a drop of phase liquid is conserved over time .
Consider an example of a harmonic oscillator in which a fluid rotates around a reference point. Obviously, the drop preserves volume, since all its movement is reduced to solid-state rotation. The drop shape remains unchanged, but this is the case for the harmonic oscillator. Consider another example. Suppose the Hamiltonian has the form H = pq.
Perhaps it will seem to you unlike the Hamiltonian, although it is absolutely correct. We derive the equations of motion:
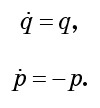
According to these equations, q increases exponentially with time, and p decreases exponentially with the same speed. In other words, the flow presses the liquid to the p axis, simultaneously and equally expanding it along the q axis. Any drop stretches along q and shrinks along p. Obviously, the drop is experiencing colossal deformations, but its phase volume does not change.
The Liouville theorem is the closest imaginable analogue of the type of irreversibility that we discussed in lecture 1. In quantum mechanics, the Liouville theorem is replaced by a quantum version, which is called unitarity. Unitarity is even more similar to what we discussed in Lecture 1, but this is the topic of the next issue of The Theoretical Minimum.
»More information about the book can be found on
the publisher's website.»
Announcement»
ExcerptFor readers of this blog 20% discount coupon -
Theoretical minimum