What is supersymmetry?
Supersymmetry is a hypothetical symmetry of space and time, and unique. Among theoretical physicists, this idea was very popular for several reasons - it was a hit when I was a student, even before physics became a cool topic, and even earlier.
The automatic consequence of the presence of symmetry in nature is that each type of particle will have one or several superpartners — a different type of particle, possessing the same properties, but differing in a certain, and important, way. If a particle is a fermion, then its superpartner is a boson. If a particle is a boson, its superpartner is a fermion (
what are fermions and bosons ).
In our world, many fermions are all particles of matter - and many bosons are all carriers of interactions. But none of these particles have any properties suitable for being someone a superpartner. Therefore, if supersymmetry were a natural symmetry, each of the types of elementary particles known to us would have to have partners until we were open. And since we know more than 20 particles, we have a lot of work!
So what is this symmetry? This is a symmetry that connects space and time with the directions of space and time of superpartners - in other words, space-time has additional dimensions, unlike those we know. In the boson dimension - we are used to them - you can move as far as you want, let's say, step by step, move to the left. In the fermion measurement, everything is arranged in such a way that only one step can be taken. If you take one more step, you will find yourself nowhere. You can only return. It sounds strange, and it is; as a result, it is necessary to determine such measurements through mathematics, and not with the help of words or analogies.
Einstein's theory of relativity copes with the description and prediction of many aspects of our world. His theory consists of a set of equations obeying a certain set of symmetries. For example, translational symmetry, or symmetry associated with transferring an experiment from one place of space-time to another: an experiment conducted today in London will give the same result as the same experiment that was conducted several months later in Tokyo. In the 1960s, it was mathematically proved that supersymmetry is the only symmetry that can be added to the symmetries of Einstein's theory so that the resulting equations do not diverge from the properties of the real world. In this sense, supersymmetry stands alone.
Where are these superparticle particles?
If supersymmetry were the exact symmetry of nature, we would have already found many superpartners.
Before proceeding further, let us remember what
elementary particles we
know . In the article on the link figure. 1 and 2 are particularly useful in order to cover particles with one glance and compare them with the figures below.
 Fig. one
Fig. oneIn fig. 1, I showed what particles would exist in the world if the Standard Model were complemented by precise supersymmetry.
• For each matter fermion, for example, an electron or a strange quark, there are two new particles - both bosons. Their names are rather ugly, the electron and strange squark, where "c" means supersymmetry. You may ask why there are two of them (and why there is only one for each neutrino). Refer to pic. 3 below, and you should all become clear.
• For boson carriers of interactions, there are partners-fermions. A photon has a photino, a gluon has a gluino, and so on. With massive W-bosons, everything is a bit more complicated. They have a wine partner [wino], as well as a Higgs partner, named H
+ (Attention! This particle should not be confused with the H
+ particle appearing in the article that tells
what it would be to the Standard Model if the Higgs field were Zero . Unfortunately, there is a constant problem in particle physics with particle naming - there are not enough letters). All these particles have exactly the same mass in this imaginary supersymmetric world.
• There are two Higgs particles in this model, h
0 and H
0 , and each has a Higgsino partner. One is massless, the second is massive. Why two? It turns out that in a supersymmetric world it is necessary to have two particles in order for the mass to appear in the upper and lower quarks in the usual way. The second argument is that two Higgsino are necessary for mathematical consistency.
But it is obvious that this ideally supersymmetric world is not ours. As shown in the figure, in such a world, particles and their superpartners:
• They interact in the same way with other particles and their superpartners.
• Possess exactly the same mass.
We would have known more than a hundred years ago about the existence of particles that would have the same electric charge and the same mass as electrons, but they would not be electrons. For example, we would have atoms with electrons, atoms with electrons, and atoms with their mixture. The number of atom types would be much larger than the observed, and since the bosons in the atoms would behave completely differently from fermions, the chemistry of the new atoms would be completely different. Data and everyday experience exclude this possibility. There are no electrons with a mass of electrons, and a point. So exact supersymmetry is not a correct theory of nature, and we knew this even before we conceived it.
End of supersymmetry? Not so fast.
Despite the seeming catastrophe, the initial theory of supersymmetry gives us a simple and plausible way out of the situation. In physics, there is a common idea that symmetries can be hidden from our gaze (physicists say they break spontaneously, but this is not a very good intuitive example — there is symmetry, it is just hard to recognize).
 Fig. 2
Fig. 2One example is rotational symmetry on Earth. The laws of nature do not depend on how the experiment will be oriented (see Fig. 2). This is true, but it is difficult to see on Earth, where it matters whether your experiment is turned with the right side up, or it is upside down, or it is tilted. But in a distant cosmos, far from planets, moons and stars, the laws of nature have rotational symmetry. Your experiment will give the same answer regardless of its orientation. By the way, measurements of light emitted by very distant atoms confirm this theory. The earth confuses us. It makes us think that the downward direction is different from the upward or leftward direction. But this apparent distinction is not a property of the laws of nature. The difference arises because of the closeness of the Earth, hiding the rotational symmetry from our view.
The question is that if some aspect of our world (not as coarse as the Earth, but some imperceptible, like the Higgs field) hides from our gaze supersymmetry throughout the Universe? What then? It turns out that it is quite easy to get the same world as ours, where the superpartners of the famous parts exist, just became harder - too heavy for us to find them in experiments.
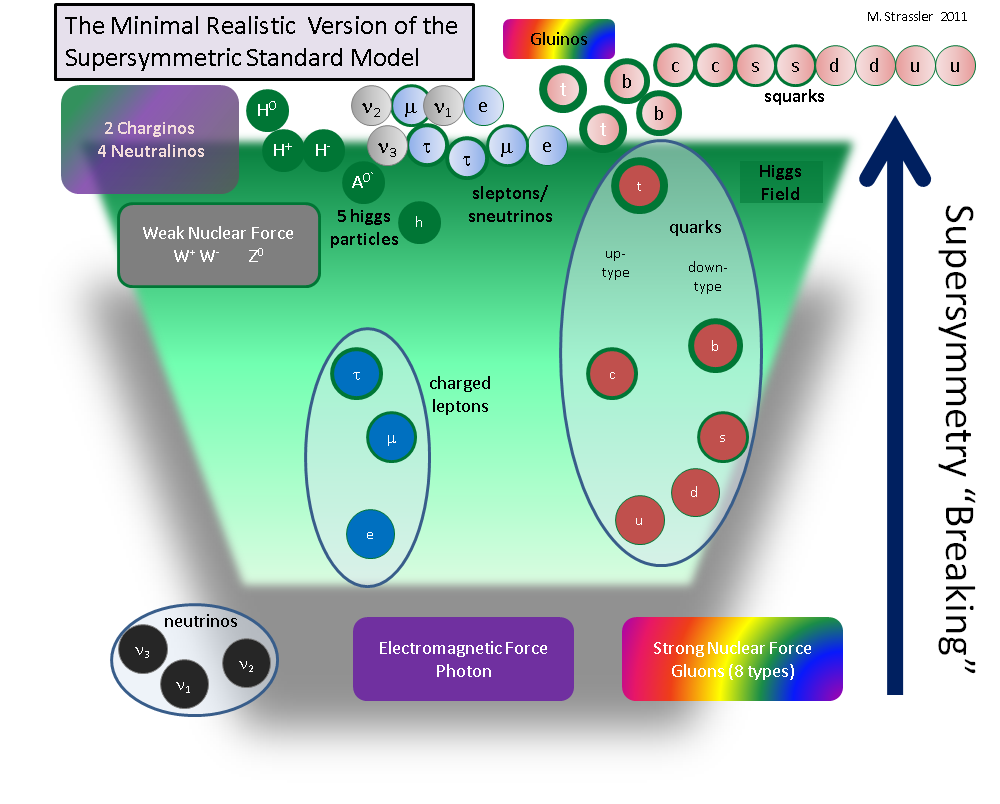 Fig. 3
Fig. 3A realistic possible world of this type — perhaps similar to ours — is shown in Figure. 3. You see that the violation of supersymmetry (that it hides and is not easy to detect) has increased the scale of the masses of all superpartners so that the entire mass scale is above the mass of the upper quark. And this is not as artificial or stupid as it seems - mathematics readily accepts this effect. There are many exact examples of how this can happen - but there are too many of them to be guessed which one is the most likely.
In this probable world I have shown for you, I made several arbitrary assumptions, but they are quite often found in the detailed examples of supersymmetry breaking studied by theoretical physicists, including myself:
• Squarks and gluino received a large mass.
• Sleptons and snatrinos received a greater mass, but probably a little less than squars and gluino.
• Wine, Zino, Photino and Higgino were mixed in a set of electrically charged particles, charginos, and electrically neutral particles, neutralino, some of which are probably slightly more massive than W and Z.
• Five Higgs particles have the broadest mass spectrum, although at least one of them is fairly light.
And this is not the only scheme that can occur when supersymmetry is broken! There are many other possibilities that I will call supersymmetry variants. But the variant I presented is the most popular among theorists and experimenters, especially in Europe (it is less popular in the USA, I don’t know about other places). There are good reasons for this popularity; it turns out that there are several independent ways to get a scheme similar to this one. However, popularity always gives rise to bias, and we need to consider all possibilities without making assumptions about these arguments.
But if superpartners are very massive, could it not be that we cannot produce any of them in the coming decades or even centuries? Are we counting the
number of angels that can fit on the needle tip ? From the foregoing, it really does mean that such a risk exists. However, there is a more subtle argument in favor of supersymmetry, thanks to which many physicists hope that all these super partners will be within the reach of the Large Hadron Collider. This follows from the fact that supersymmetry would solve the problem of hierarchy - one of the greatest mysteries of our world.
An important property of nature that baffles scientists, and among them me, is the property of the hierarchy - a huge difference between the properties of weak nuclear interaction and gravity. This hierarchy can be described in several different ways, each of which rests on one of its properties. For example:
The mass of the smallest possible black hole determines what is known as the
Planck mass . A more accurate way to determine this quantity is a combination of the Newtonian gravitational constant G, the quantum [reduced] Planck constant ħ and the speed of light c: the Planck mass is
The masses of particles W and Z carrying weak nuclear interaction are approximately 10,000,000,000,000,000 times smaller than the Planck mass. In this regard, there is a huge hierarchy of mass scales between weak nuclear interaction and gravity.
Faced with such a huge number as 10,000,000,000,000,000, ten quadrillions, physicists naturally ask the question: where did it come from? And he can have a rather interesting explanation.
But trying to find this explanation in the 1970s, physicists saw the existence of a serious problem, even a paradox, hiding behind this number. This problem, now known as the hierarchy problem, is related to the size of the non-zero Higgs field, which in turn determines the mass of the particles W and Z.
The non-zero Higgs field has a size of about 250 GeV, this gives a mass of particles W and Z equal to about 100 GeV. But it turns out that it follows from quantum mechanics that such a size of the Higgs field is unstable, it is something like (incomplete analogy!) Of a vase balancing on the edge of the table. From the physics known to us, from quantum jitter, it seems to be that for the Higgs field there must exist two natural meanings - by analogy with two natural places for a vase, either standing firmly on the table, or wallowing broken on the floor. And it turns out that the Higgs field seems to be either zero, or it should be comparable in size to the Planck energy, 10,000,000,000,000,000 more than the observed value. Why does its meaning turn out to be non-zero and so tiny, so, at first glance, unnatural?
This is the problem of hierarchy.
Many theoretical physicists have devoted a significant part of their careers to attempts to solve this problem. Some argued that we need new particles and new interactions (their ideas pass under the names supersymmetry, technicolor, small Higgs, etc.) Some said that our understanding of gravity is wrong, and that there are new, unknown dimensions (“additional dimensions ") Spaces that we will discover in the near future in experiments on the LHC. Others say that there is nothing to explain here, since the selection effect works: the Universe is much larger and more diverse than the part we observe, and we live in a rather unnatural part of the Universe mainly because its remaining part is unsuitable for life - just like , in spite of the fact that stony planets are rare, we live on one of them because only here could we evolve and survive. Perhaps this problem has other, not yet invented solutions.
Many of these solutions — certainly all solutions with new particles and interactions, and with new dimensions — predict that new phenomena can be seen at the LHC. And gradually, but inexorably, the LHC excludes these possibilities one by one. So far, we have not seen any unexpected events. But we are only at the beginning.
By the way, you can often read how the hierarchy problem is associated with the mass of the Higgs particle. This is not true. The problem is that the value of the non-zero Higgs field is too large. Strictly speaking, quantum mechanics corrects not the Higgs mass, but the square of the Higgs mass, changing the potential energy of the Higgs field, and, consequently, the magnitude of the field, and makes it zero or too large. This is a disaster, since the masses W and Z are known. The Higgs mass is unknown, so it could be very large - if the masses W and Z would also be large. So the problem lies in the masses of W and Z - and in the magnitude of the non-zero Higgs field, a problem both from a logical and from a scientific point of view.