Neutrinos - just like charged leptons (electron, muon, tau), quarks of the upper type (upper, enchanted, true) and lower types (lower, strange, charming) - are of three types. But they can be divided into types in different ways. At the same time, due to the quantum nature of our world, only one of them can be used at one time. In this article I will explain why this is happening, and how this fact implies such an interesting and scientifically important fact as
neutrino oscillations .
You may think that every particle has a certain mass - for example, the electron mass energy is (E = mc
2 ) 0.000511 GeV - and from one of the possible points of view, three types of neutrinos are not exceptions. We can classify three neutrinos by their masses (which are not yet precisely known), and call them, from the lightest to the heaviest, neutrino-1, neutrino-2 and neutrino-3. We will call such a division mass classification, and such types of neutrinos - mass types.
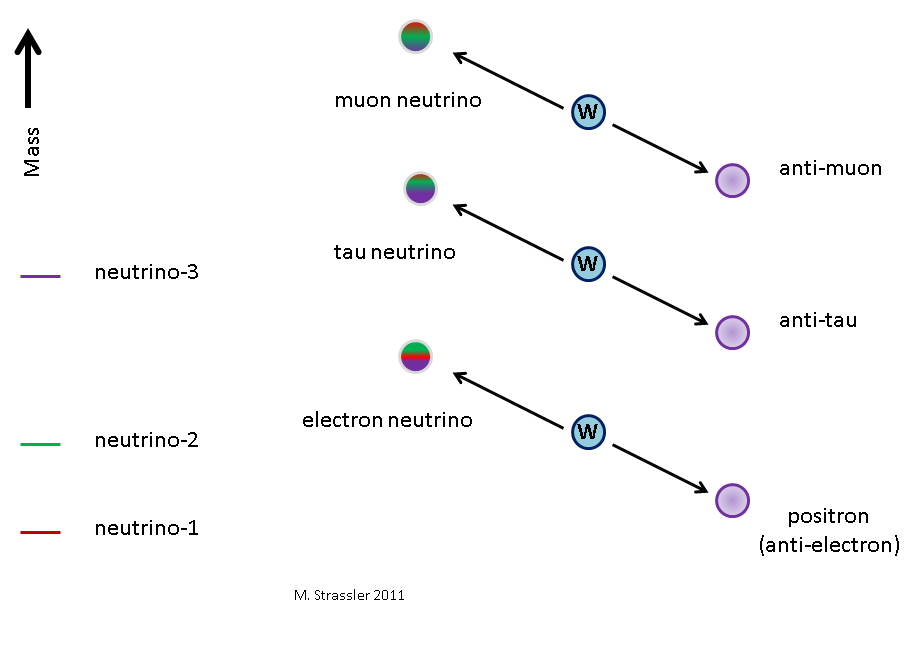 Fig. one
Fig. oneAnother way to classify neutrinos is by their association with charged leptons (electron, muon, and tau). This is mentioned
in the article on how particles would look if the Higgs field were zero. The best way to understand this is to focus on how a weak nuclear interaction affects the neutrino, which is reflected in their interactions with the W particle. The W particle is very heavy, and if you produce it, it can break up (Fig. 1) into one of the three charged antileptons and one of the three neutrinos. If W splits into an antitau, then a tau neutrino will appear. Similarly, if W decays into an antimuon, a muon neutrino will appear. (Which is critical for creating a neutrino beam, the pion decays with the help of weak interactions, and anti-muon and muon neutrino are obtained from positively charged pions). And if W decays into a positron, an electron neutrino will appear. We call this a weak classification, and these neutrinos are weak-type neutrinos, since they are determined by the weak interaction.
Well, what's the problem? We constantly use different classifications applied to people. We say that people are young, old and old; they are high, medium height and low. But people can optionally be divided further, for example, into nine categories: young and tall, young and medium height, adults and low, elderly and low, and so on. But quantum mechanics forbids us to do the same with neutrino classifications. There are no neutrinos that are both muon neutrinos and neutrino-1; there is no tau neutrino-3. If I tell you the mass of the neutrino (and, therefore, whether it belongs to the group of neutrinos-1, 2 or 3), I just can not tell you whether it is electronic, muon, or tau-neutrino. A neutrino of a certain mass type is a mixture, or “superposition” of three neutrino of a weak type. Every mass-type neutrino - neutrino-1, neutrino-2 and neutrino-3 - is an exact, but different from the other mixture of electron, muon and tau neutrinos.
The reverse is also true. If I see how a pion breaks up into an anti-muon and neutrino, I will immediately find out that the resulting neutrino will be a muon neutrino - but I cannot find out its mass, since it will be a mixture of neutrino-1, neutrino-2 and neutrino-3 . Electronic neutrino and tau-neutrino are also exact, but differing mixtures of three neutrinos of certain masses.
The connection between these mass and weak types is more similar (but not exactly corresponds to) the connection between the classifications of American highways, as going "north to south" and "west to east" (the US government divides them in this way, assigning odd numbers of the C / Yu and even simple roads Z / V), and dividing them into roads going from “northeast to southwest” and from “southeast to northwest." The use of any classification has its advantages: the C / U - H / V classification is suitable if you concentrate on latitude and longitude, and NE / SW - SE / NW will be more convenient near the coast, since it goes from south-west to north-west. East. But both classifications cannot be used simultaneously. The road to the northeast is partly north, and partly east; we can not say that it is either such or syaya. And the north road is a mixture of the north-east and north-west. The same with the neutrino: a mass-type neutrino is a mixture of weak-type neutrinos, and a neutrino of a weak type is a mass mixture. (The analogy will stop working if you decide to use the improved classification of the S / Yu-SV / YuZ-V / Z-YuV / SZ roads; there is no such option for neutrinos).
The impossibility to classify neutrinos, attributing them to a certain mass type and to a certain weak type is an example of the
principle of uncertainty , similar to strangeness, which prohibits simultaneously knowing the exact position and exact velocity of a particle. If you know exactly one of these properties, you have no idea about the other. Or you can learn something about both properties, but not all. Quantum mechanics tells you exactly how to balance your knowledge and ignorance. By the way, these problems do not apply only to neutrinos. They are associated with other particles, but are especially important in the context of the behavior of neutrinos.
A few decades ago everything was easier. It was then believed that the neutrino had no mass, so it was enough to use a weak classification. If you look at old works or old books for ordinary people, you will see only such names as electron neutrino, muon neutrino and tau neutrino. However, after the discoveries of the 1990s, this is no longer enough.
And now the fun begins. Suppose you have a high-energy electron-type neutrino, that is, a certain mixture of neutrino-1, neutrino-2 and neutrino-3. Neutrinos move in space, but its three different mass types move at slightly different speeds, very close to the speed of light. Why? Because the speed of an object depends on its energy and mass, while the three mass types have three different masses. The difference in their speeds is extremely small for any neutrino that we can measure - it has never been observed - but its influence is surprisingly strong!
Neutrino speed difference - some formulas
The particle velocity v in Einstein's theory of relativity can be written in terms of the particle mass m and energy E (this is the total energy, that is, the energy of motion plus mass energy E = mc
2 ), and the speed of light c, like:
If a particle has a very high speed and its total energy E is much greater than the mass energy mc
2 , then
Where dots remind that this formula is not exact, but a good approximation to large E. In other words, the speed of a particle moving at almost the speed of light differs from the speed of light by an amount equal to half the square of the ratio of the particle mass energy to its total energy . From this formula it is clear that if two neutrinos have different masses m
1 and m
2 , but the same high energy E, then their speeds differ very little.
Let's see what that means. All measured neutrinos from a supernova exploded in 1987 on Earth in a 10-second interval. Suppose the electron neutrino was emitted by a supernova with an energy of 10 MeV. This neutrino was a mixture of neutrino-1, neutrino-2 and neutrino-3, each of which was moving at a slightly different speed! Would we notice it? Neutrino masses are not exactly known to us, but let's say that neutrino-2 has mass energy equal to 0.01 eV, and neutrino-1 has mass energy equal to 0.001 eV. Then their two speeds, given that their energies are equal, will differ from the speed of light and from each other by less than one part from one hundred thousand trillion:
(the error of all equations does not exceed 1%). Such a difference in speed means that parts of neutrino-2 and neutrino-1 of the original electron neutrino would have arrived on Earth with a difference of a millisecond - such a difference for many technical reasons cannot be detected.
* * *
And now from the interesting we turn to really strange things.
This tiny difference in speeds makes the exact mixture of neutrinos-1, neutrinos-2 and neutrinos-3, a component of the electron neutrino, gradually change when moving in space. This means that the electron neutrino from which we started, with time, ceases to be itself and correspond to one particular mixture of neutrino-1, neutrino-2 and neutrino-3. The various masses of the three mass types of neutrinos transform the initial electron neutrino in the process of moving into a mixture of electron neutrino, muon neutrino and tau neutrino. The percentages of the mixture depend on the difference in speeds, and, consequently, on the energy of the initial neutrino, as well as on the difference in mass (more precisely, on the difference in squares of mass) of neutrino.
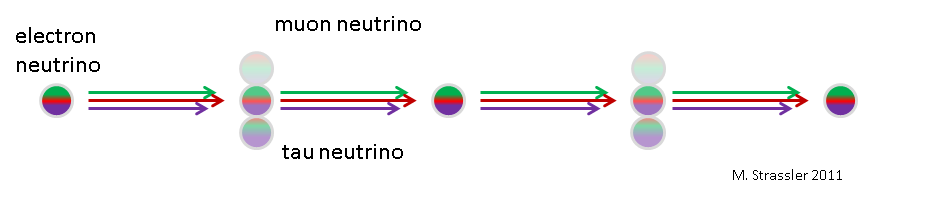 Fig. 2
Fig. 2At first, the effect increases. But, interestingly, as shown in Fig. 2, this effect is not just constantly growing. It grows, and then decreases again, and then grows again, decreases again, again and again, in the process of neutrino movement. This is called neutrino oscillations. How exactly they occur depends on the mass of the neutrino and how the mass neutrino and the weak neutrino are mixed there.
The effect of oscillations can be measured due to the fact that an electron neutrino can collide with a nucleus (and this is how a neutrino can be detected) can turn into an electron, but not into a muon and not a tau, while a muon neutrino can turn into a muon, but not into an electron or tau. So, if we started with the beam of a muon neutrino, and after moving a certain distance, some neutrinos collided with nuclei and turned into electrons, this means that oscillations occur in the beam, and muon neutrinos turn into electronic neutrinos.
One very important effect complicates and enriches this story. Since ordinary matter consists of electrons, but not of muons and tau, electron neutrinos interact with it not in the same way as muon or tau. These interactions occurring through weak interactions are extremely small. But if the neutrino passes through a large mass of matter (for example, through a tangible portion of the Earth or the Sun), these small effects can accumulate and greatly affect the oscillations. Fortunately, we know enough about the weak nuclear interaction in order to predict these effects in detail, and calculate the entire chain backwards, from measurements in an experiment to finding out the properties of neutrinos.
All this is done using quantum mechanics. If this is not intuitive for you, relax; for me this is also not intuitive. I got all the intuition available from the equations.
It turns out that careful measurement of neutrino oscillations is the fastest way to study the properties of neutrinos! For this work have already given the Nobel Prize. This whole story emerged from the classical interaction of experiment and theory, stretching from the 1960s to the present day. I will mention the most important measurements.
To begin with, we can study the electron neutrinos produced in the center of the Sun, in its well-studied nuclear furnace. These neutrinos travel through the sun and through the empty space to the Earth. It was found that when they arrive on Earth, they are equally likely to belong to the type of muon or tau, as well as to the type of electronic neutrino. This in itself serves as evidence of neutrino oscillations, and the exact distribution gives us detailed information about neutrinos.
We also have muon neutrinos arising from the decay of pions arising in cosmic rays. Cosmic rays are high-energy particles arriving from space and colliding with atomic nuclei in the upper atmosphere. The resulting cascades of particles often contain pions, many of which decay into muon neutrinos and antimuons, or muon antineutrinos and muons. We detect some of these neutrinos (and antineutrinos) in our detectors, and we can measure how many of them belong to electron neutrinos (and antineutrinos) depending on the thickness of the Earth that they passed before they hit the detector. This again gives us important information about the behavior of the neutrino.
These "solar" and "atmospheric" neutrinos taught us a lot about the properties of neutrinos over the past twenty years (and the first hint of something interesting happened almost 50 years ago). And to these natural sources of energy are added various studies carried out with the help of neutrino rays, such as those used in the
OPERA experiment, as well as with the help of neutrinos from conventional nuclear reactors. Each of the measurements is largely consistent with the standard interpretation of solar and atmospheric neutrinos, and allows for more accurate measurements of mixtures of mass types and weak types of neutrinos and differences in mass mass neutrino squares.
As one would expect, in experiments there are small discrepancies with theoretical expectations, but none of them was confirmed, and most, if not all, are just statistical coincidences or problems at the experimental level. So far, no contradiction with the understanding of neutrinos and their behavior has been confirmed in several experiments. On the other hand, this whole picture is rather new and rather poorly verified, therefore it is quite possible, although it is unlikely that it can have completely different interpretations. And indeed, quite serious alternatives have already been proposed. So, clarifying the details of the neutrino properties is an actively developing field of research in which, for the most part, there is agreement, but some questions still remain open - including a complete and irrevocable definition of the neutrino masses.