In the 20th century, particle physics experts found that it was very important to take into account all possible symmetries that can demonstrate the laws of nature that govern elementary particles. The presence or absence of symmetry can reveal to us aspects of nature that are otherwise not obvious.
From the set of possible symmetries one can distinguish three that play unique roles:
charge conjugation (C),
spatial parity (P), and
symmetry with respect to time reversal (T). Three of these transformations affecting particles, space, and time include:
• C: replacement of all particles with particles with opposite charge (both electric charge and less familiar charges; even some neutral particles are replaced. For example, neutrinos change to antineutrinos, and neutrons to antineutrons).
• R: placing the world in a mirror (more precisely, changing the orientation of three dimensions to the opposite).
• T: launching the world in the reverse direction of time (more precisely, changing the direction of time evolution).
Each of these transformations has the property that if you hold it twice, you will return to the original state. In jargon, we say that P
2 = P × P = 1 (that is, if you put a mirror in a mirror, what you see will look the same as if there were no mirrors), and, similarly, C
2 = 1 and T
2 = 1.
In addition, you can perform two conversions together. For example, you can do C, and then R, which we simply write as “CP” (or you can do RS, it will be the same - the order does not matter for these transformations), in which you put the world in the mirror and change particle charges. You can consider CT, PT, and even CPT. Just like C, P and T themselves, any of these combinations, when performed twice, return everything as it was.
And what do we do with these transformations? We need to ask ourselves: if we represent the world created from ours with the help of one of the transformations, will the laws of nature governing elementary particles and interactions in it work in the same way as in ours?
If the answer is yes, then everything that can happen in a new, transformed world can happen in ours; in this case, we say that this transformation is a symmetry of our world. More precisely, it is the symmetry of the laws of the nature of our world. If not, then the transformation can still be carried out, but this will no longer be the symmetry of our world, because the world received after the transformation will be different from ours.
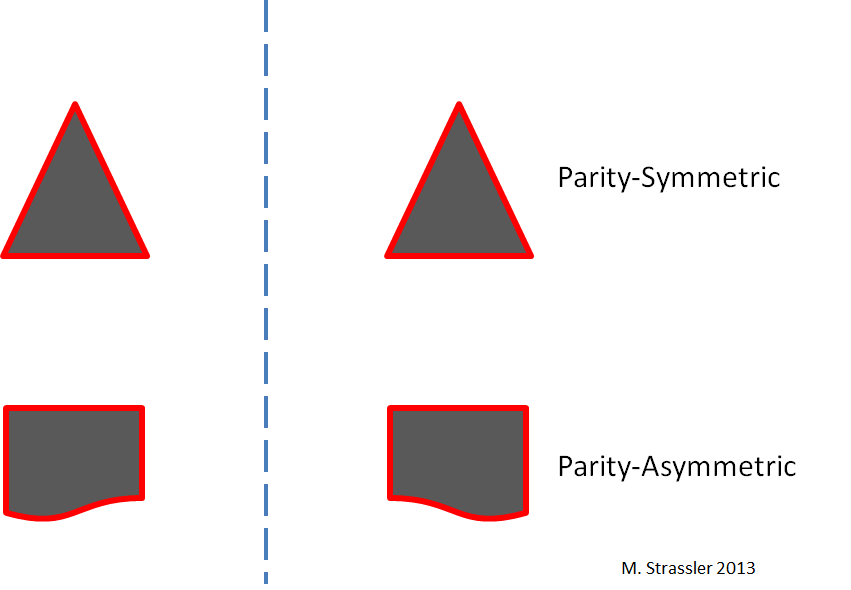 Fig. one
Fig. oneIt's pretty easy to understand how spatial parity (P) works. A certain object may or may not have parity symmetry. As shown in fig. 1, the reflection of a triangle in a mirror gives us a triangle identical to the first one, so that the triangle will be symmetrical with parity. But the more complex form shown in fig. 1, does not look exactly the same after reflection, so it is asymmetrical in parity.
Obviously, our world is not symmetrical in the mirror, it can be seen on any photograph of nature (see Fig. 2). However, it is necessary to distinguish between the symmetry of an object and the symmetry of the laws of nature that govern all possible objects. The basic processes of particle physics can be symmetrical, which would mean that for any process that can occur in nature, there is a mirror process that can also occur (Fig. 2, below).
But it turns out that the basic processes of nature are not symmetrical in P!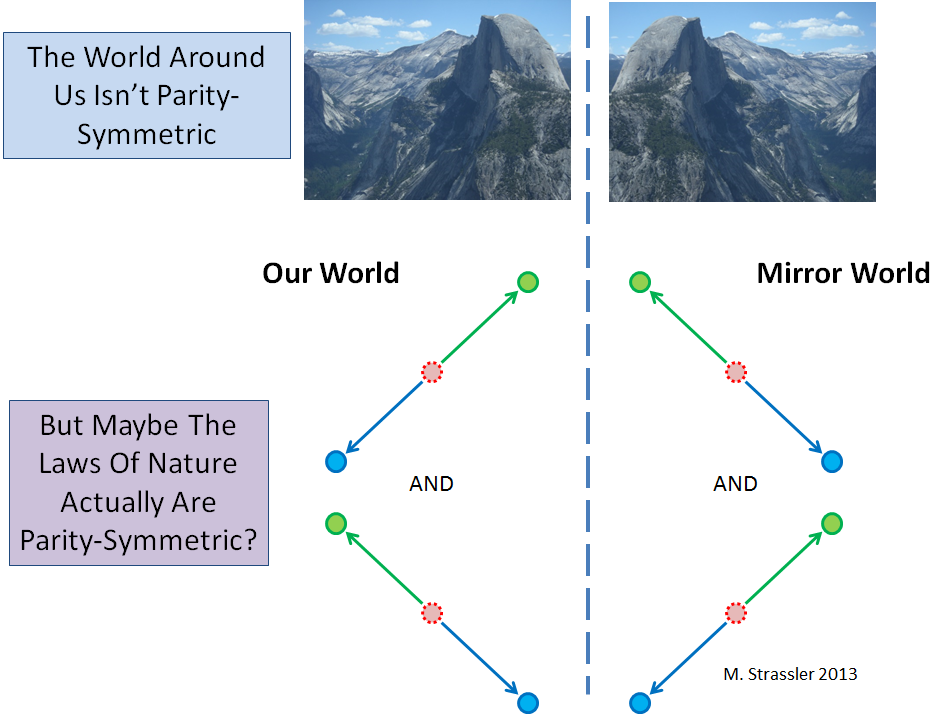 Fig. 2
Fig. 2The striking fact is that neither C, nor P, nor T, nor CP, nor CT, nor PC are nature symmetries. The main processes known to physics before the twentieth century — in particular, including gravitational and electromagnetic interactions, that is, all those that hold the Earth together and retain its orbit around the Sun, and those that control the physics of atoms and molecules and all chemistry — are symmetrical. C, P, and T. So physicists were quite surprised when in the 1950s and 1960s they found that weak nuclear interaction breaks all these symmetries. The only transformation that is still considered (for good reasons) symmetrical for nature will be CPT.
Note that if CPT is symmetry, then the effects of CP and T should be the same. Since this is symmetry, applying the CPT transform takes you back to the same world you started with, but you also know that if you apply the T transform two times, you return to the same world you started with, then CP must do the same thing that makes T. The same is true for pairs CT and P, and for RT and C.
CPT transforms particles and their interactions in our world into antiparticles and their interactions in the transformed world, and vice versa. And, since in our world, every type of particle has an antiparticle (it happens that it is itself), and since every interaction of different particles has anti-interaction with antiparticles (so to speak), it is considered that this is ideally symmetrical. More precisely, for any world whose particles obey quantum field theory, the mathematics used in the Standard Model equations describing all known particles and interactions can be shown that CPT is symmetry. (Is this so for a unifying theory, such as string theory, combining the quantum theory of gravity with non-gravitational forces, it is difficult to say; but in the experiments, no violation of the CPT has yet been obtained).
C and P are not of symmetry due to weak nuclear interaction
Until the 1950s, everything that was known to physicists — all chemistry and atomic physics, all the effects of gravity and electromagnetic interaction, light waves and the foundations of the atomic nucleus — corresponded to a world symmetrical in R. But it turns out that C and P are not nearly symmetrical laws of nature. They are violated as often as possible by weak nuclear interactions.
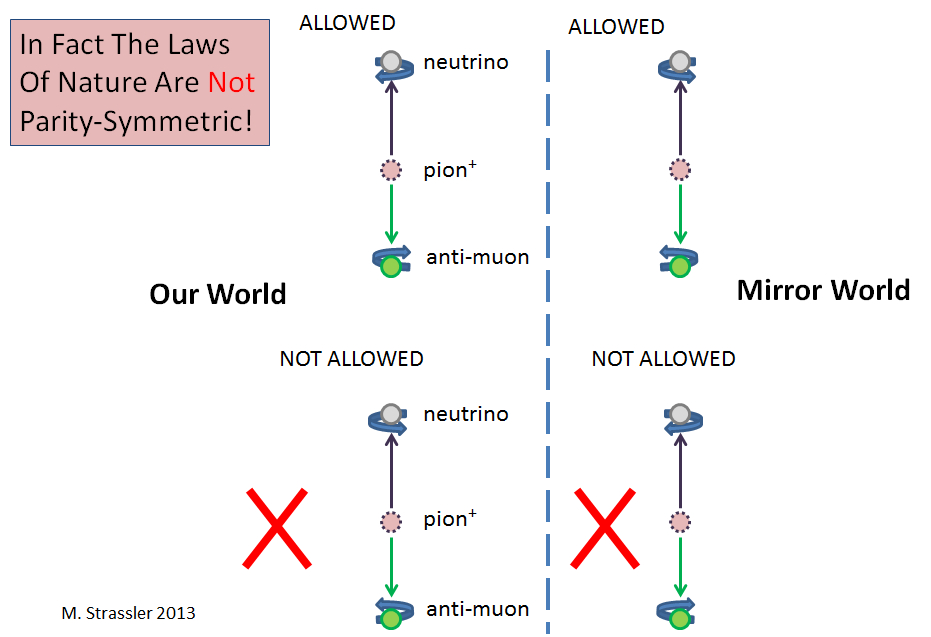 Fig. 3
Fig. 3In the simplest (but not the only) example, neutrinos are involved. When a neutrino appears in the physical process, it is always created with the help of weak nuclear interaction. And when it occurs, it always turns counter-clockwise from the point of view of the observer at the point from where it originates. (Neutrinos, like electrons and protons and many other particles, in some sense always spin; more precisely, they always have a rotational moment). In other words, it rotates like a left-side screw (Fig. 3). (In the jargon, he will have a negative helicity). But a neutrino produced by a weak nuclear interaction never spins like a right-handed propeller. Since P would change right and left places (as in a mirror), this means that weak nuclear interaction violates R.
In a more specific example (Fig. 3), when a positively charged pion (hadron consisting of an upper quark, an anti-lower quark and a set of gluons and quark / antiquark pairs) splits into an anti-muon and a neutrino, the neutrino is always left-sided and never right-handed. This violates R. And when a negatively charged pion falls into a muon and an antineutrino, the antineutrino is always right-sided. This difference in processes, including negative and positively charged pions, is disturbed by C.
Violation of P and C of this type is now quite clear. The Standard Model (the equations we use to describe all known particles and interactions) includes it in a rather natural way, and the details of the equations have been thoroughly tested in experiments. So, although P and C violations were a huge surprise in the 1950s, today they are a standard part of particle physics.
However, if we look at the particles themselves (and do not go into the details of their interactions), the SR (the same as the RS) seems symmetrical at first glance. This is because P turns the spin of a neutrino from left-side to right-hand, but C reverses the charge of the pion, turns the anti-muon into the muon and replaces the neutrino with the antineutrino; the final process takes place in our world (Fig. 4). So for some time, physicists believed that weak nuclear interaction would save the CP, although separately it violates both C and R.
Another way to see this is to read
my article on how particles would look if the Higgs field were zero. It shows that, for example, the electron-left and neutrino-left particles go together and are exposed to weak isospin interaction, and the electron-right particle goes separately from the neutrino-right, and none of them undergoes a weak isospin interaction. In this case, what is true for the electron-right particle, is true for the positron-right particle, and what is true for the positron-right particle is true for the electron-left. But P changes the electron-left and electron-right particles, so obviously, this is not symmetry; C changes the electron-left and positron-left, and since the positron-left particle is not affected by the weak interaction, C is also not a symmetry. However, the CP changes the electron-left and positron-right particles, and both of them are subject to weak nuclear interaction.
 Fig. four
Fig. fourSR is also not symmetry
But in the 1960s, it turned out that the CP is also broken by weak nuclear interactions. This was again a surprise, clear for today, but still explored by us. Here is the story in brief.
Most hadrons (particles consisting of quarks, antiquarks, and gluons) almost instantaneously decay by means of strong nuclear interaction, for periods less than a trillionth of a trillionth of a second. One hadron, proton, is stable; the neutron itself lives 15 minutes. (Atomic nuclei consisting of protons and neutrons are often also called hadrons, but personally I prefer to call them “sets of hadrons”). But several hadrons, which have historical and practical importance, have a life time, though short, but not very much - from a billionth of a trillionth of a second to a billionth of a second - and most of them collapse due to weak nuclear interactions (other decay through electromagnetic interaction). And in some of them — especially mesons containing one lower quark or one lower antiquark — decays violating the CP were measured. Other signs of SR violation are in oscillations between two hadrons, similar to neutrino oscillations.
This type of CP violation is very interesting because it occurs naturally where there are three or more flavors or generations of upper quarks (upper, enchanted and true) and three flavors of lower quarks (lower, strange and charming). As Kobayashi and Maskawa pointed out, in the version of the Standard Model containing only two generations, there could not have been such a violation of the SR; he should have had a completely different reason. Since they observed this much earlier than the discovery of the third generation of particles, they essentially predicted the need for a third generation, for which they were subsequently awarded the Nobel Prize in Physics in 2008 (along with Nambu for his great work in other fields).
So far, there are no signs of violation of CP, having a nature different from that determined by Kobayashi and Maskawa. But if there are particles and interactions besides those known to us in the Standard Model, there may be other conditions where CP is violated.
However, even inside the Standard Model there is one big mystery.
Strong nuclear interaction and CP
It is very unexpected that SR is not significantly disturbed by strong nuclear interaction, and no one knows why this is so. We know that the strong interaction does not violate the SR very strongly due to the specific properties of the neutron, known as the
electric dipole moment .
The neutron is an electrically neutral hadron, very similar to a proton. The quarks, antiquarks, and gluons that make up the neutron are held together by strong nuclear interactions. For any electrically neutral moment, you can ask an interesting question - does it have an electric dipole?
The magnet that you played with as a child is a magnetic dipole, which has a north and south pole (Fig. 5). A magnetic monopole would be either the north pole or the south pole; but you have never seen such a thing, and no one has seen it. The electric dipole, however, has zero electric charge, but on the one hand it has a positive, and on the other, a negative charge. This can be such a simple case as a hydrogen atom, with an electron in the role of a negative charge and a proton in the role of a positive one.
For a simple electric dipole consisting of two charges separated by a distance D, one of which has a charge q, and the other - -q, the electric dipole moment is simply defined as q × D. Note that if a positive and negative charge sit in one place, then such an object has no dipole moment; charges must be separated in space so that it is "polarized." The hydrogen atom is usually not polarized. But many molecules have a dipole moment, although they are electrically neutral. For example, the water molecule H
2 O has a dipole moment of 3.9 × 10
-8 e cm in size, where “e” is the proton charge (-e is the electron charge), and cm is 1 centimeter. For comparison, this is only slightly less than what can be obtained by expanding the electron and proton by a distance approximately equal to the size of the water molecule (such a dipole moment would have about 9 × 10
-8 e cm). This suggests that the electrons of two hydrogen atoms in H
2 O spend a lot of time with an oxygen atom.
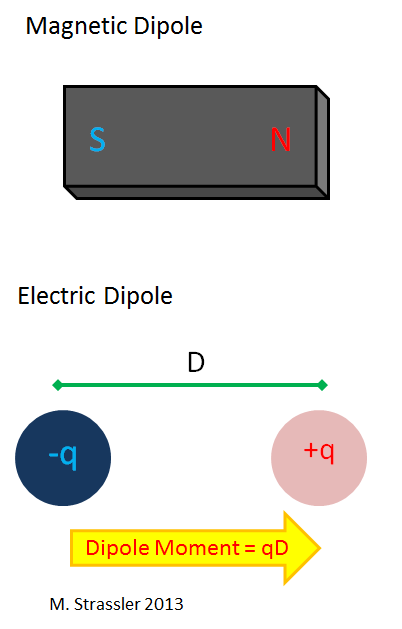 Fig. five
Fig. fiveHow big can the neutron dipole moment be? The neutron radius is about 10
-13 cm, so one would expect D to be about the same. And it consists of quarks, antiquarks and gluons; Gluons are electrically neutral, but quarks and antiquarks have electric charges: 2/3 e (upper quark), –1/3 e (lower quark), –2/3 e (upper antiquark) and +1/3 e (lower antiquark ). So one would expect q to be like this. It turns out that one would expect that the magnitude of the electric dipole moment of the neutron will be within 10
-13 e cm. This is a million times smaller than the dipole moment of the water molecule, mainly because the neutron radius is less than a million times.
In fact, some non-obvious effects give us an estimate of an even smaller size. Real expectation is in the region of 10
-15 e cm.
But if the neutron has an electric dipole moment, it would break T, and therefore the CP, if the CPT can be considered at least an approximate symmetry (it also breaks P). So, if the CP and the CPT were exact symmetries, then the neutron's electric dipole would have to be zero.
Of course, we already know that CP is not an exact symmetry; it violates the weak nuclear interaction. But the weak interaction is so weak (at least with respect to neutrons) that it can give the neutron an electron dipole moment of the order of 10
-32 e cm. This is much less than we can measure! So, for our purposes, it can be considered zero.
But if the strong interaction that holds the neutron together breaks the SR, then we expect that the magnitude of the electric dipole moment will be 10
-15 e cm. However, the experiment shows that the electric dipole moment of the neutron is less than 3 × 10
-26 e cm! This is ten thousand million times less than expected. Therefore, a strong nuclear interaction does not disturb the SR as much as was supposed.
Why is it so much less than expected? No one knows, although there were many assumptions. This riddle is called the
strong CP problem and is one of the three greatest problems that torment particle physics, along with the
problem of hierarchy and the
problem of the cosmological constant .
Specifically, the problem is as follows. If we write down the theory of strong nuclear interaction — the equations for gluons, quarks, and antiquarks, called QCD — then these equations will contain different parameters, namely:
• The unifying force of strong nuclear interaction
• masses of different quarks,
• theta angle that does not affect the Feynman diagrams, but, nevertheless, determines the effects of various subtle processes (quantum tunneling,
instantons , pseudoparticles) of gluon physics.
Stop what? What is the last point? Well, this additional parameter QCD was opened in the 1970s (this is one of the areas in which
Alexander Polyakov became famous, who recently won an award). The problem itself is too technical to describe here, but suffice it to say that if the theta angle is not 0 or π, then a strong nuclear interaction breaks the CP. More precisely, CP breaks a certain combination of theta angle and masses of different quarks (specifically, the product of the complex phases of their masses). And these two parameters (theta angle and quark masses) do not have an obvious connection - so how do they combine in such a way that they are perfectly compensated? However, for some reason, their combination is zero, or at least ten billion times less than it could be. There are no obvious reasons for this.
This riddle by the age of almost 40 years can be the following explanations:
• , ( , ; , , ).
• ,
, ; , 30 , . , , .
, ; , , .