
The theory of relativity fascinates with its paradoxes. We all know about the twins, about the possibility of shoving a long plane in a short box. Today, every graduate of the school knows the answers to these classic riddles, and even physics students believe that they have no secrets in the special theory of relativity.
Everything would be fine if it were not for the depressing circumstance - the impossibility of superluminal speeds. Could it not be faster ?! - I thought in my childhood. Or maybe you can? Therefore, I invite you to a session, I really do not know, the black or white magic of the name of Albert Einstein with the revelation at the end. But for those who seem a little, I have also prepared a puzzle.
UPD: A day later I publish the decision. A lot of text formulas, graphs at the end.
To Alpha Centauri
I invite you to take a seat in our interstellar ship, which is heading towards Alpha Centauri. 4 light years away from the end point of the route. Attention, we start the engines. Go! For the convenience of passengers, our captain set such a thrust so that we accelerate with the magnitude

and felt the usual force of gravity on Earth.
Here we are already well overclocked, let up to half the speed of light

. It seemed a simple question to ask: how fast will we approach Alpha Centauri in our own (ship) frame of reference. It would seem simple if we fly with speed

in the fixed frame of reference of the Earth and Alpha Centauri, then from our point of view we are approaching the target at a speed

.
The one who has already felt the trick is absolutely right. Answer

is wrong! Here it is necessary to make a clarification, under the speed of approaching Alpha Centauri, I call the change in the remaining distance to it, divided by the time interval over which such a change occurred. Everything, of course, is measured in our reference system associated with the spacecraft.
Here we must remember about the Lorentz length reduction. After all, speeding up to half the speed of light, we find that the scale along the direction of our movement shrank. Let me remind the formula:
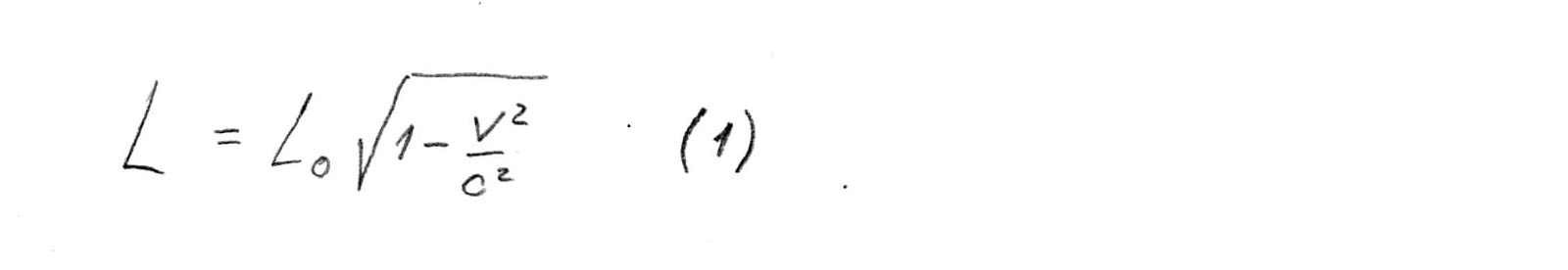
And now, if at a speed of half the speed of light, we measure the distance from Earth to Alpha Centauri, we did not get 4 ss. years, and only 3,46 years.
It turns out that only due to the fact that we accelerated to

we have already reduced the distance to the end point of the journey by almost 0.54 over. And if we do not just move at high speed, but also accelerate, then the time factor will appear at the scale factor, which in fact also has an approaching speed and adds to

.
Thus, in addition to our usual, I would say classic, speed

one more member is added - a dynamic reduction in the length of the remaining path, which occurs if and only if there is a non-zero acceleration. Well, let's take a pencil and count.
And those who are too lazy to follow the calculations meet on the other side of the spoiler
- the current distance to the star in the ruler of the ship’s captain,

- time on the clock in the mess,

- speed.

Already here we see that the first partial derivative is speed, just speed

with a minus sign, as soon as we approach Alpha Centauri. But the second term - the same catch, which I suspect, not everyone thought.
To find the time derivative in time in the second term, you need to be careful, because we are in a moving frame of reference. The easiest way to calculate it on the fingers is from the formula for the addition of relativistic velocities. Let at the moment of time

we are moving with speed

, and after some period of time they increased our speed by

. The resulting speed according to the formula of the theory of relativity will be

Now we gather together (2) and (3), and the derivative of (3) must be taken at

because we consider small increments.
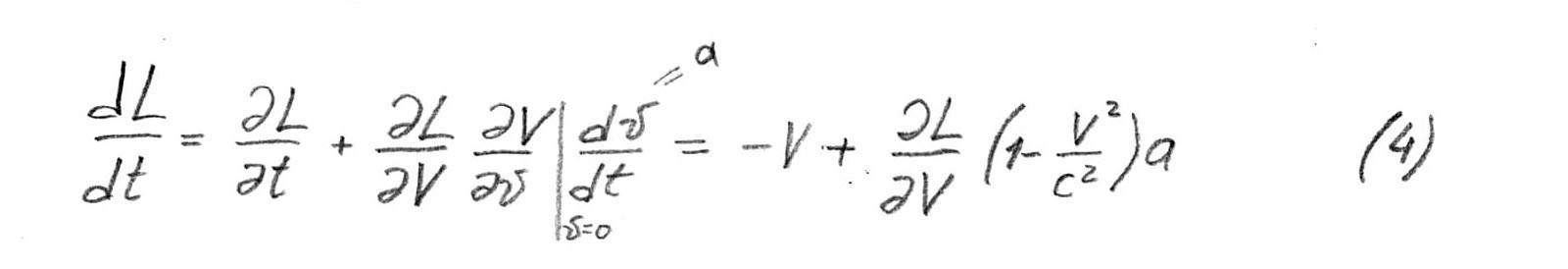
We admire the final formula
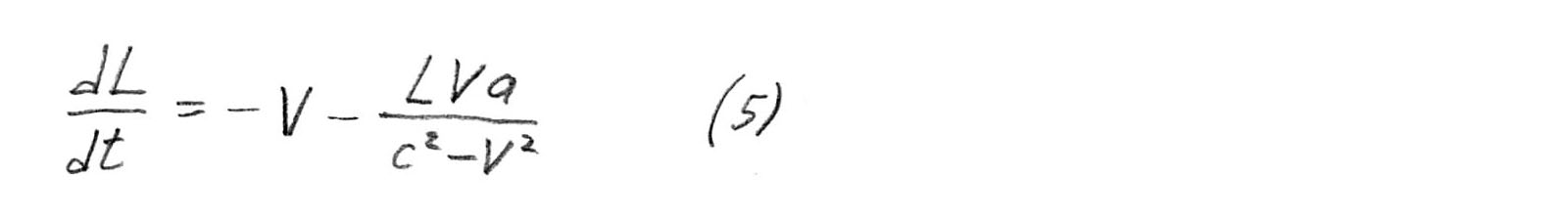
She is amazing! If the first term - speed - is limited by the speed of light, then the second term is not limited by anything! Take

more and ... the second term can easily exceed

.
- I'm sorry, what! - some will not believe.
- Yes, yes, exactly, - I will answer. - It can be more than the speed of light, more than two speeds of light, more than 10 speeds of light. To paraphrase Archimedes, I can say: “give me a suitable

and I will provide you with an arbitrarily large speed. ”
Well, let's substitute numbers; numbers are always more interesting. As we remember, the captain set the acceleration

and the speed has already reached

. Then we find that when

light year, our speed of approach equals the speed of light. If we substitute

light years then

The copy: "three whole, three-tenths of the speed of light."
We continue to be surprised
Let's look more closely at formula (5). After all, it is not necessary to sit down in a relativistic spacecraft. Both speed and acceleration can be quite small. It's all about magic

. Just think about it!
So I got into the car and pressed the gas. I have speed and acceleration. And at this very moment I can guarantee that somewhere around a hundred or so millions of light years ahead of me there are objects that are approaching me now faster than light. For simplicity, I have not yet taken into account the speed of the Earth in its orbit around the Sun, and the Sun around the center of the Galaxy. Taking them into account, objects with a superluminal velocity of approximation will be already very close - not on a cosmological scale, but somewhere on the periphery of our Galaxy.
It turns out that involuntarily, even with minimal acceleration, for example, getting up from a chair, we are participating in superluminal motion.
Still surprised
Look at the formula (5) very, very closely. Let's find out not the speed of approaching Alpha Centauri, but rather the speed of moving away from Earth. When large enough

For example, halfway to the goal, we can find that both the Earth and Alpha Centauri are approaching us. Recovering from surprise, of course, you can guess that the reason for the reduction in length, which works not only forward, but also backward. Space behind the stern of a spacecraft shrinks faster than we fly away from the starting point.
It is easy to understand and another amazing effect. After all, it is necessary to change the direction of acceleration, as the second term in (5) immediately changes the sign. Those. The speed of approximation can easily become zero, or even negative. Although the usual speed

we will still be sent to Alpha Centauri.
Exposing
I hope I got you confused enough. As so, we were taught that the speed of light is maximum! You cannot approach anything faster than the speed of light! But here you should pay attention to the proclamation to any relativistic law. It is in any textbook, but it seems that it is only cluttering up the wording, although it is in it all the “salt”. This proverb says that the postulates of the special theory of relativity work "in the inertial frame of reference."
In a non-inertial frame of reference, Einstein does not guarantee us anything. So it goes!
The same, a little more detail and a little more complicated.The formula (5) contains the distance

. When it is zero, i.e. when we try to determine the speed of locally relatively close objects, only the first term remains

which, of course, does not exceed the speed of light. No problem. And only at large distances, i.e. not locally, we can get superluminal speeds.
It must be said that, generally speaking, the relative speed of objects distant from each other is a poorly defined concept. Our flat space-time in an accelerated reference frame looks curved. This is the famous "Einstein elevator" equivalent to a gravitational field. And it is correct to compare two vector quantities in a curved space only when they are at one point (in one tangent space from the corresponding vector bundle).
Speaking of our paradox of superluminal speed, you can argue in a different way, I would say integrally. After all, a relativistic journey to Alpha Centauri will take an astronaut’s own hours of much less than 4 years, so if we divide the initial distance by our own time, we will get an effective speed more than the speed of light. In essence, this is the same twin paradox. To whom it is convenient, can precisely and understand superluminal movement.
That's the whole trick. Your Captain's Evidence.
And finally, I came up with your homework
or a draft for discussion in the comments .
Problem
Earthlings and alpha-centaurs decided to exchange delegations. A spacecraft has started from Earth at a speed of

. Simultaneously with him from Alpha Centauri, the flying saucer of aliens went to meet with the same speed.

What is the distance between the ships in the reference system of the earthlings' ship at the moment of launch, when they were at the Earth and Alpha Centauri, respectively? Write the answer in the comments.
UPD: Solution
So the solution to the problem. First, consider it qualitatively.
We agree that the clock on Alpha, Earth, the rocket and the plate are synchronized (this was done in advance), and the start for all four hours took place at 12:00.
Consider space time graphically in resting coordinates.

. The earth is at zero, Alpha is at a distance

on axis

. Alpha Centauri's world line obviously just goes vertically upwards. The world line of the plate goes with an inclination to the left, because she flew out of the point

in the direction of the Earth.
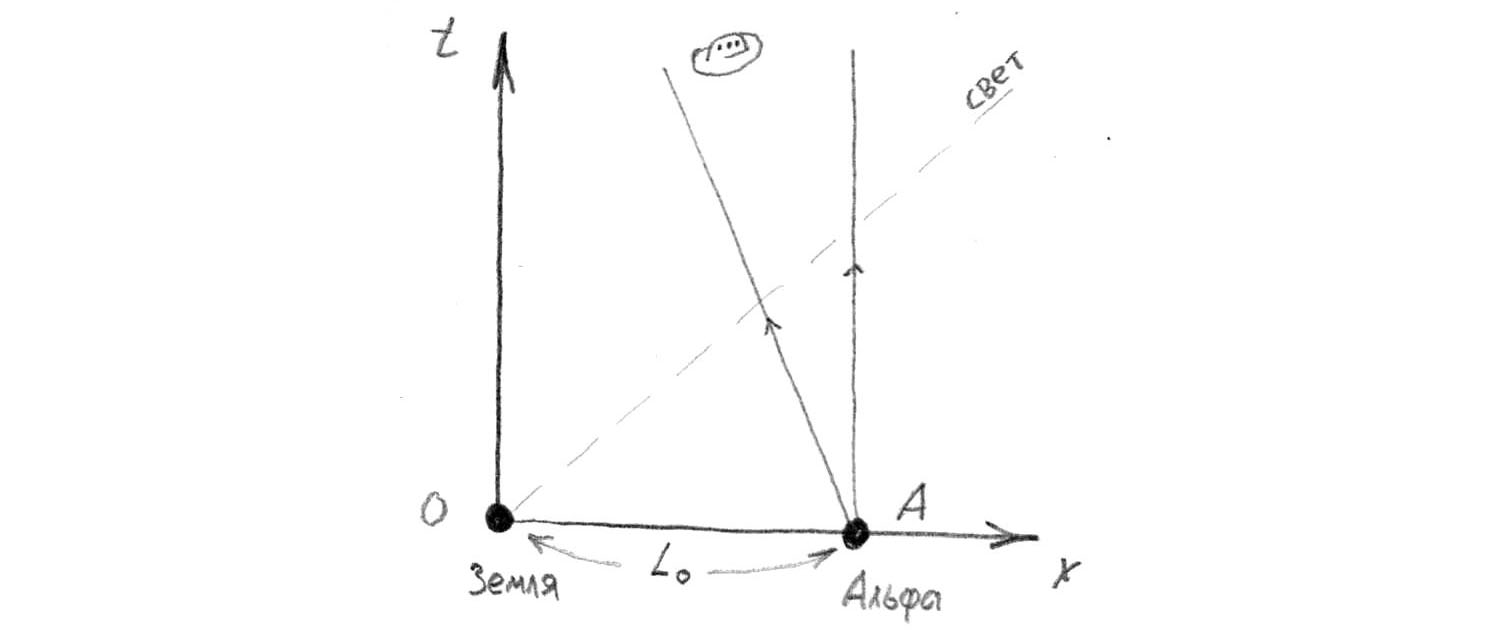
Now, on this graph, we will plot the coordinate axes of the reference system of the rocket launched from the Earth. As is known, such a transformation of the coordinate system (CK) is called a boost. When this axis is tilted symmetrically relative to the diagonal line, which shows the light beam.
I think at that moment everything became clear to you. See axis

crosses the world lines of alpha and flying saucer at different points. What happened?
An amazing thing. Before the start, from the point of view of the rocket, the plate and the Alpha were at the same point, and after speeding up, it turns out that the launch of the rocket and the plate was not simultaneous in the SC. The plate, it turns out, started earlier and managed to get a little closer to us. Therefore, now at 12:00:01 the clock on the rocket is closer to the plate than to Alpha.
And if the rocket accelerates, it will “jump over” to the next SC, where the plate is even closer. Moreover, such an approximation of the plate occurs only due to the acceleration and dynamic compression of the longitudinal scale (which is what all my post is about), and not the rocket moving in space, because the rocket is still in fact nothing to fly. This approximation of the plate is the second term in the formula (5).
Well, among other things, we must take into account the usual Lorentz contraction of the distance. Immediately tell the answer that at the speeds of the rocket and the plates at

every distance
- between rocket and alpha: 3,46 sv. years (usual Lorentz contraction)
- between rocket and plate: 2.76 sv. of the year
Who cares, let's conjure with formulas in four-dimensional spaceSuch tasks are conveniently solved using four-dimensional vectors. There is no need to be afraid of them, everything is done using the most common actions of linear algebra. Moreover, we move only along one axis, therefore only four coordinates remain from four coordinates:

and

.
Next, agree on a simple notation. The speed of light is considered equal to unity. We physicists always do that. :) Another usually considered the unit is Planck's constant and gravitational constant. Essentially, this does not change, but damn facilitates scribbling.
So everywhere present "relativistic root" we denote the gamma factor for the compactness of records, where

- Earth rocket speed:

Now we write in the components vector

:

The upper component is time, the lower is spatial coordinate. Ships start simultaneously in a fixed system, so the upper component of the vector is zero.
Now we find the coordinates of the point

in the moving coordinate system

i.e.

. To do this, use the transformation to a moving frame of reference. It is called boost and is done very simply. Any vector must be multiplied by the boost matrix.

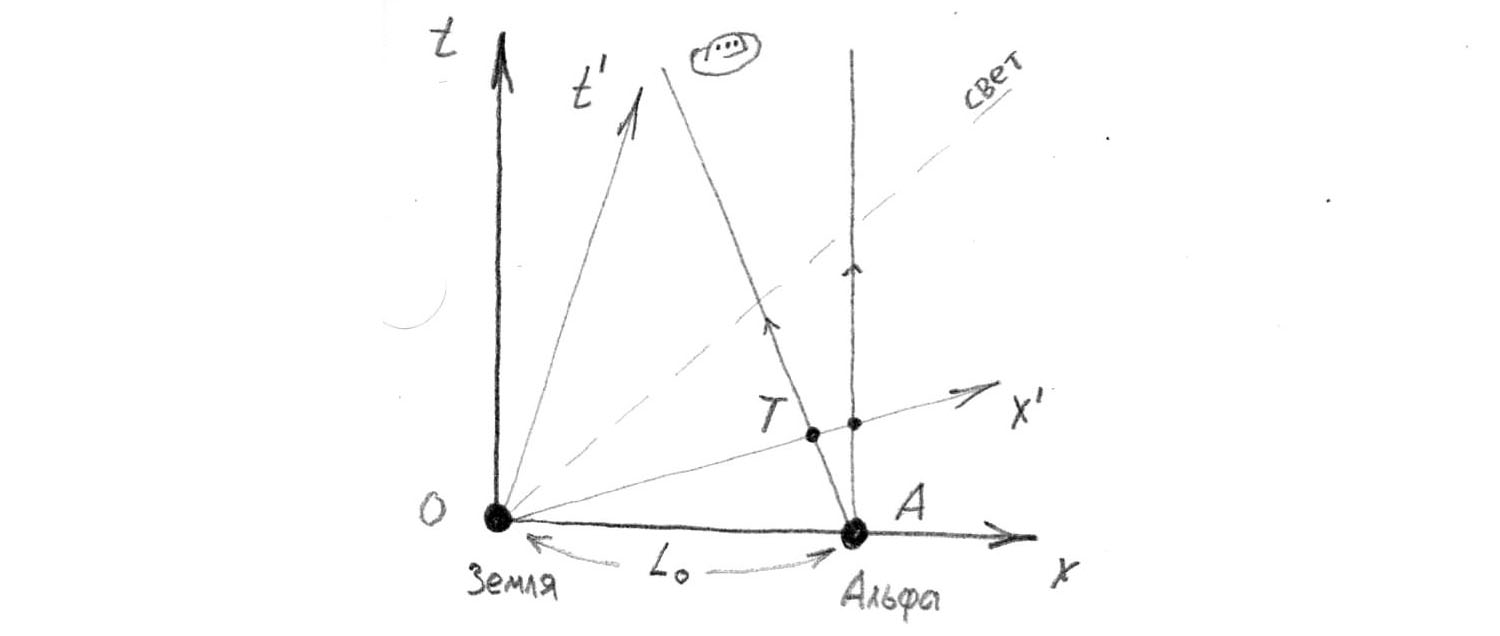
Multiply:
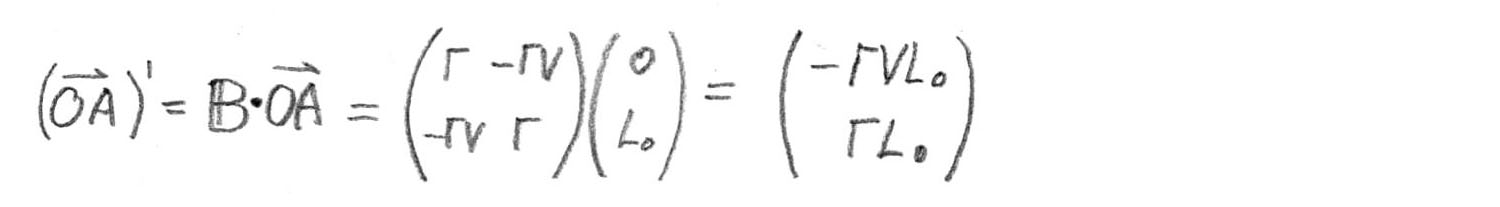
As we see, the time component of this vector is negative. This means that the point

in terms of moving the rocket is under the axis

i.e. in the past (as seen in the figure above).
Find a vector

in a fixed system. The time component is some unknown time period.

, spatial - the distance that the plate is approaching in time

moving with speed

:

Now the same vector in the system

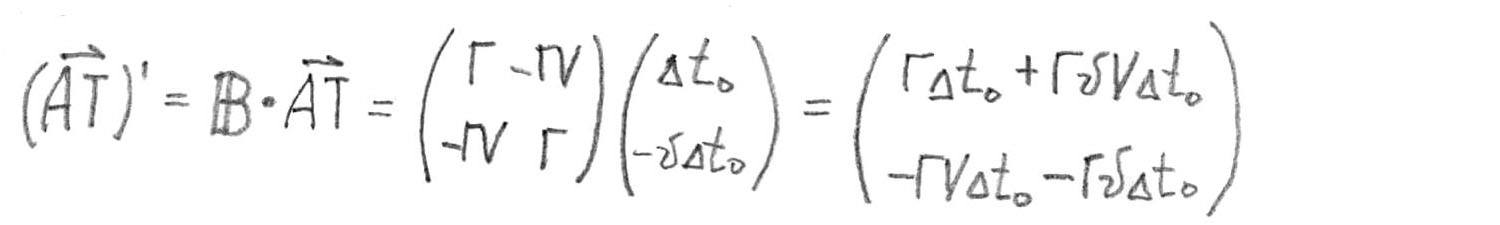
Find the usual vector sum

Why did I equate this amount to the right of such a vector? By definition point

is on the axis

therefore the temporary component

should be equal to zero, and the spatial component - this will be the desired distance

from rocket to plate. From here we obtain a system of two simple equations — we equate the time components separately, the spatial components separately.
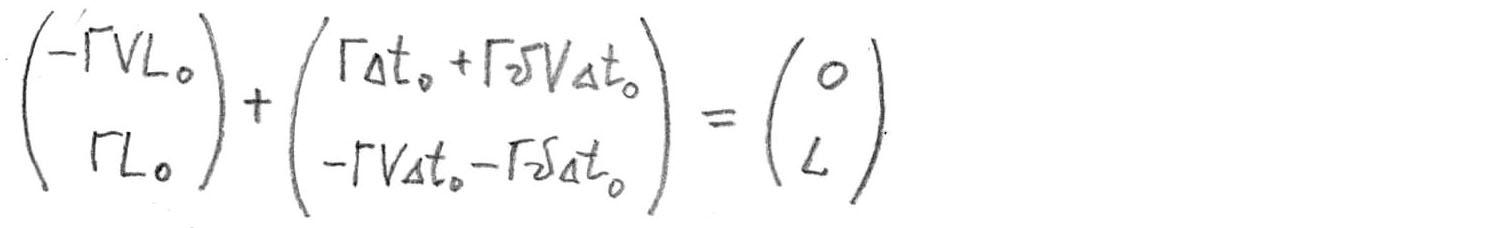
From the first equation, we determine the unknown parameter.

, substitute it into the second equation and we get

. Let me omit simple calculations and write immediately

Substituting

,

get
