In this article, I will tell you something about how quantum mechanics works, in particular, about the amazing phenomenon called “quantum fluctuations”, and how it is used in quantum field theory, an example of which is the Standard Model (equations used by us for predictions of the behavior of known elementary particles and interactions). A deep understanding of this phenomenon and the energy connected with it leads us straight to one of the most serious and unresolved conflicts in science: the problem of the cosmological constant. It also leads us to the riddle of naturalness, or to the
problem of hierarchy .
In quantum field theory, quantum fluctuations are sometimes called or described as "the appearance and disappearance of two or more virtual particles." This technical jargon turns out to be very unfortunate, because these things (no matter how we call them) are definitely not particles - for example, they do not have a certain mass - and also, since the concept of a “virtual particle” is precisely defined in the presence of relatively weak interactions. .
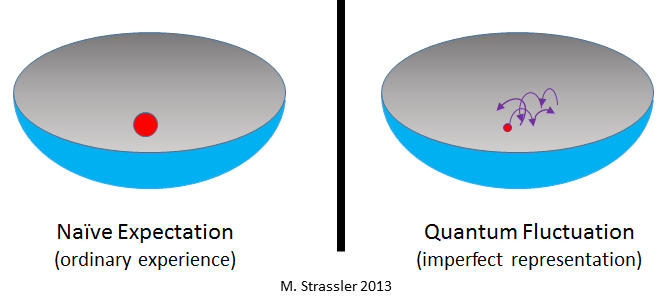 Fig. one
Fig. oneQuantum fluctuations are closely related to the Heisenberg uncertainty principle. Here is a classic, simplest example (Fig. 1). If you place the ball on the bottom of the bowl, it will endlessly remain there alone. This can be expected based on everyday experience. And in the absence of quantum mechanics it would have been like that. But if you put a very light particle in a tiny bowl or a different type of trap, you will find that it does not sit at the bottom. If it were still below, it would violate the principle of uncertainty - ensuring that you cannot know exactly where the particle is (that is, at the bottom) and how it moves (in our case it does not move). This can be imagined, albeit imperfectly, but it is practical, as a kind of constant jitter, which affects the particle and does not allow it to calm down, as intuition tells you by the example of balls and bowls. One useful aspect of this imperfect picture is that it makes it clear that energy can be associated with this tremor.
In quantum field theory - quantum equations for fields, such as electric, a similar effect is observed. Let me explain it.
Fluctuations of quantum fields
Each elementary particle (and I am now talking about real particles) in our Universe is a ripple, a small wave, a wave of the lowest possible intensity, traveling along the corresponding elementary quantum field (Fig. 2). The particle W is a wave in the field W; photon - a wave in an electric field; top quark - a wave in the top quark field.
And if there are no particles? Even where, as we believe, there is only empty space, the fields still exist - they sit quietly for themselves, just as there is water in the pond, even if neither the wind, nor the pebbles cause ripples on its surface, and like in a room there is air, even if there are no sounds.
 Fig. 2
Fig. 2However, the thing is that these fields never behave absolutely quietly. Quantum fields do not support a constant value; their value at any point in space always shakes a little. Trembling is called "quantum fluctuations," and just like for a particle in a tiny bowl, it is a consequence of the famous "Heisenberg uncertainty principle." You cannot find out the value of the field and at the same time change it; your knowledge of one of these quantities, and usually two, must be imperfect. And these fluctuations are also sometimes explained as the reason for the presence of two or more “virtual particles”, but this name is associated only with technical aspects (with calculations of the properties of fluctuations using the famous
Feynman diagrams ), and does not say how you need to imagine it.
The obvious question is: are you sure of the presence of quantum field fluctuations? Answer: yes, although for the time being I will not explain it. One example: quantum fluctuations cause the interaction force to float when you measure it at shorter and shorter distances - and we not only observe this effect, it also coincides with high accuracy with what we can calculate Standard Model. This success confirms not only the presence of quantum fluctuations, but also the detailed structure of the Standard Model, up to distances of the order of one million millionth millionth of a million meters. Another example: the reaction of an electron to a magnetic field can be measured with an accuracy of one trillion; it can also be calculated using the Standard Model with an accuracy of one trillion, assuming the presence of fluctuations in the fields we know. Surprisingly, the measurements coincide with the calculations of the Standard Model.
What is important, this trembling generates a certain amount of energy - quite a lot. How many? The better your microscope (or particle accelerator), the more jitter you see, and the more jitter energy you detect.
Consider a box with an edge of one meter and ask: how much energy associated with the jitter of one quantum field can be counted in this box (Fig. 3)?
Calculation 1: let's say, as shown by our experimental measurements at the Large Hadron Collider, the Standard Model - a working description of all processes occurring at distances greater than one millionth millionth millionth of a meter - let's call this the “TANK distance” equal to about 1/1000 of the proton radius Since approximately such a scale of experiments can be carried out at the LHC - processes are available that include collisions of elementary particles with energies less than 1000 mass energies of the proton (of the energy that E = mc
2 ). This energy is the typical mass energy of the heaviest particle that can be hoped to detect when protons collide in the LHC, so let's call it “LBW energy”. Toda the amount of energy of fluctuations of each field in the Standard Model (for example, the electric field) is as follows: in each cube with the size of edges equal to BAK distance there is BAK energy. In other words, the energy density is one BAC energy per one BAK volume.
Compare this with ordinary matter, whose energy density is equal to several mass energies of a proton or neutron (that is, the mass energies of the atomic nucleus) per atom, whose volume, since a proton or neutron is 100,000 times smaller than the radius of an atom, is 1,000,000,000,000,000 times the volume of the proton. (Recall that the atom is relatively much more empty than the solar system). This means that the energy density of quantum fluctuations of the electric field is roughly one million million million times greater than that of ordinary matter, therefore the mass energy of the electric field fluctuations with an edge per meter is about one million million million times greater than the energy contained in a cubic meter of solid matter. And how much energy is it? Enough to blow up an entire planet, or even a star! It is comparable in magnitude with the total energy of the sun. Of course, this energy from the vacuum can not be released, neither for evil nor for good, so do not need to worry - it is not dangerous. But this is enough to understand the magnitude of the problem of the cosmological constant.
Calculation 2: let's say, how does this relate to the issue of the hierarchy problem and the naturalness of the Universe, that the Standard Model describes all the processes of particle physics down to the scale on which gravity becomes a strong interaction - so-called? the Planck length, which, in turn, is still a thousand million million times shorter than the distance from calculation 1. Then the amount of electric field fluctuation energy contained in a cubic meter is greater than in calculation 1
(1,000,000,000,000,000)
4 = 1 with 60 zeros
time.
If you take this number and multiply it with the number from the calculation of 1, you will have enough energy to blow up all the stars in all the galaxies in the visible part of the Universe many many many times. And it is precisely this energy that is contained in each cubic meter - if the Standard Model correctly describes physical processes on scales up to the Planck length.
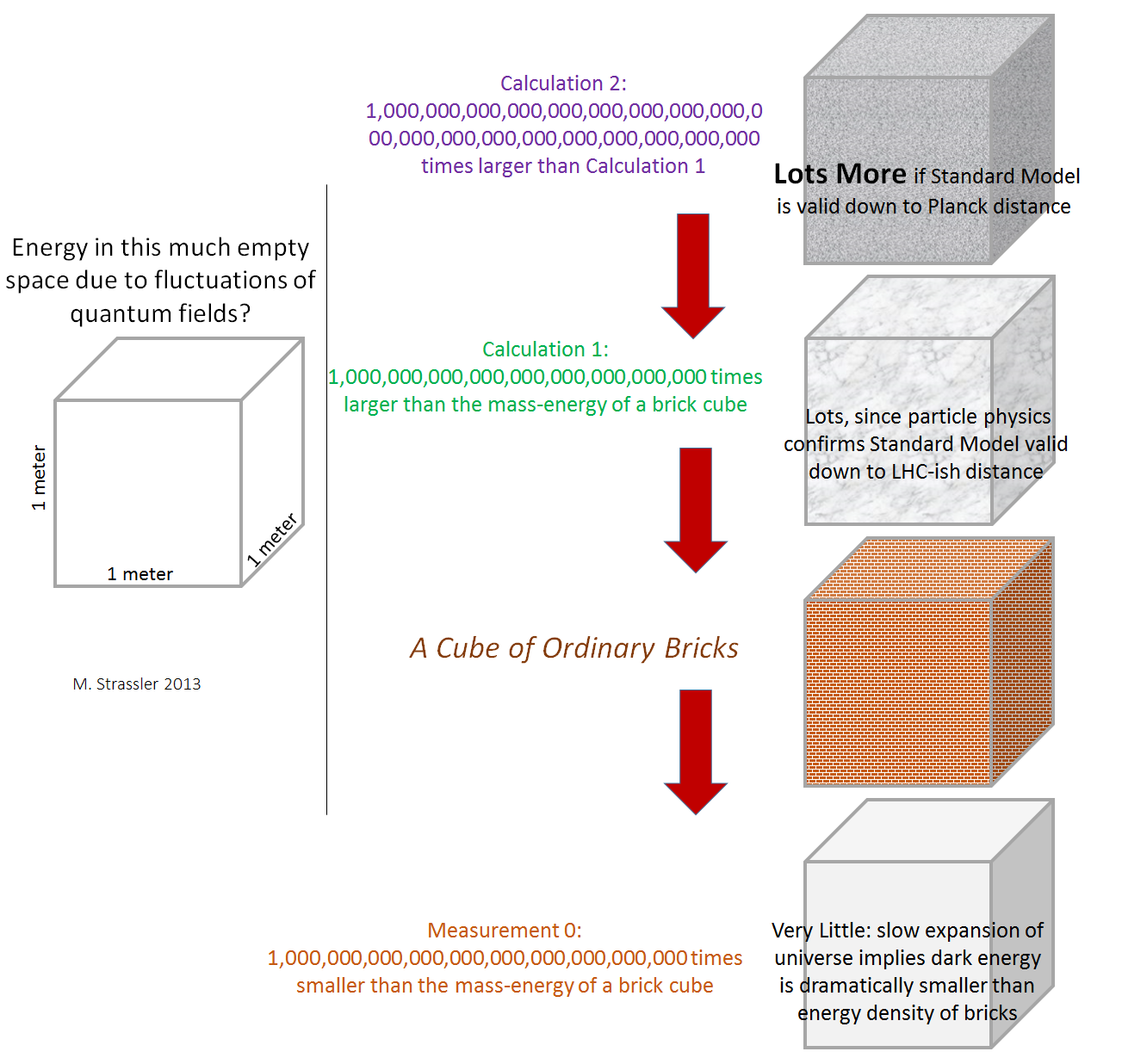 Fig. 3
Fig. 3In general, if the Standard Model (or any typical quantum field theory without special symmetries) is valid up to scales of length L, then the fluctuation energy in a cube of size L
3 is approximately equal to hc / L for each field, where h is Planck's constant, and c - universal speed limit, known as the "speed of light." This means that the energy density is approximately equal to hc / L
4 - if L decreases 10 times, then the energy density increases 10,000 times! That is why the numbers in calculations 1 and 2 turned out so huge.
These statements may seem strange to you. They are strange - but after all, quantum physics is full of oddities. Moreover, neither quantum mechanics nor quantum field theory yet let us down. As I mentioned earlier, we have full evidence that the simplest calculations, similar to those given above, work fine in quantum field theory. The fact of the existence of quantum fluctuations together with their energy is so deeply embedded in quantum mechanics that, in order to declare them false, you will need to explain a whole library of experimental results that quantum mechanics made correct predictions to. So, as with scientists, we have no choice but to take these calculations seriously and try to understand them.
You may have a couple of obvious questions: why can't we just determine if this energy is there or not? Why all this enormous energy does not act in any way on ordinary matter and on ourselves? The first part of the answer: since each cubic meter of space contains the same amount of energy, inside and outside of any cube (Fig. 4), which you can draw. Analogy: there is air pressure inside the house, but the house does not explode because of this, as long as there is equal air pressure outside the house. In the same way, the fact that this density energy of tiny quantum fluctuations is constant throughout space and time means that it does not have any effect on objects that rest or move through it. Only changes of energy in time or in space will act on particles, on atoms consisting of these particles, on people and planets consisting of these atoms. And indeed, this energy of quantum fluctuations is the same everywhere and always, therefore it is impossible to feel, try or use it.
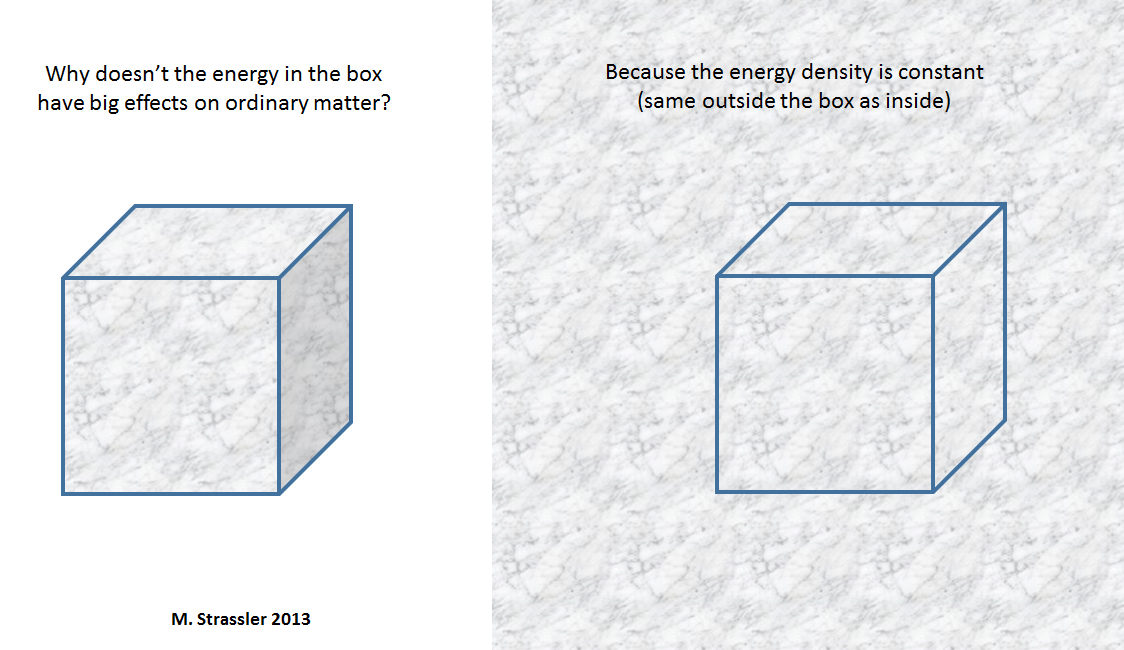 Fig. four
Fig. fourBut! The answer, part 2: although in Newtonian gravity, in which gravity attracts masses, this energy of empty space does not manifest itself, in Einstein's version, where gravity attracts energy and momentum, this will not be the case. Whether counting 1, or counting 2, or something in between, such a huge amount of energy in every cubic meter of space — what is often called “dark energy” —will cause the Universe to expand at tremendous speed! This mechanism led to “cosmic inflation”, a phase through which the universe may have passed a long time ago, which made it so uniform as we see it today. The fact that the Universe does not expand at tremendous speed suggests that the density of the energy of space should be much less than the density of energy of ordinary matter, and not much more. In each cubic meter of empty space there is only the energy of the mass of one atom, and in the cubic meter of solid matter contains the energy of the mass of the set of atoms - approximately 1 with 30 zeros. The fact that in empty space the energy density is apparently very small, in spite of all our calculations of how much it should be due to quantum field fluctuations of which we know - and there is the father and mother of all the great mysteries of quantum physics: cosmological constant problem.
The next obvious question is: are you sure that quantum fluctuations actually have energy, or perhaps it is not there, which could eliminate the problem of the cosmological constant? Answer: Yes, I am sure that quantum fluctuations have energy. It is called zero energy, and it is fundamental to quantum mechanics, thanks again to the uncertainty principle. And this can be verified: in a cunning experiment, energy can be made to work thanks
to the Casimir effect , which was predicted in the 1940s, first observed in the 1970s and more accurately tested in the 1990s. However, there are disputes over whether it is actually related to our topic.
The problem of cosmological constant is very serious. We know experimentally that the Universe is not expanding at an incredible speed; she does it rather slowly; this will be measurement 0 in fig. 3 (bottom). Therefore:
• Or, this calculation (and even calculation 1, which does not make any assumptions about what is unknown to us from the Standard Model) is somehow erroneous, and there is no such energy,
• Or the effect of this energy on the expansion of the Universe is not the same as we think, because we misunderstand gravity,
• Either the calculation is correct, but he answers the wrong question in some way we do not understand.
No one knows for sure. I will talk about possible solutions to this problem in a separate article on the cosmological constant. But I mentioned one interesting solution that definitely does not work, since it will be related to another topic.
Can the energy of different fields be mutually destroyed?
There is such a clever idea of how to get rid of this energy. It turns out that:
• The fluctuation energy of boson fields (fields for photon, gluon, W, Z and Higgs, and even graviton) is positive,
• The energy of fluctuations of fermion fields (fields for an electron, muon, tau, three neutrinos and 6 quarks) is negative!
So, perhaps, although the energy of each field is huge, when you sum up the energy of all fields, then the total energy will be zero - or at least very small?
You can do these calculations, and in the Standard Model you will see that this does not work; there are too many fermions, and there must be a huge amount of negative energy in empty space.
One of the cool things about the theory of
supersymmetry is that it forces you to add exactly the particles that you need (superpartners for each of the known types of particles) so that you automatically get this mutual destruction! And, in fact, it is the only kind of theory known to humanity in which this is possible.
Unfortunately, in reality this does not solve the problem of the cosmological constant. If supersymmetry does not manifest itself explicitly [and in our world it is impossible - the masses of all known particles must be identical to the masses of their hypothetical superpartners, and then we would have found them a long time ago], then this mutual destruction works only partially. A partial annihilation capable of disproving tally 2 still leaves you with a huge amount of energy from tally 1. As noted in fig. 3, this gigantic amount of energy is enough for the Universe to behave quite differently from what we see, if only something is wrong with Einstein's theory of gravity.
In short, today nobody knows the tricky way to automatically mutually destroy the energy density of fluctuations of various fields in the world described by the Standard Model right up to the BAK distances. In fact, no one even knows how to do this in any slightly non-supersymmetric quantum field theory (and still, the combination of supersymmetry with gravity revives this problem).
In other words: even if one admits the existence of a special mutual annihilation between the boson fields of nature and the fermionic fields of nature, it appears that such mutual annihilation can occur only by chance, and in a very, very small fraction of quantum field theories or quantum theories of any type (including string theory ). Thus, only a very, very tiny part of the universes that can be imagined can at least approximately resemble ours with you (or at least that part of it that we can observe with the help of our eyes and telescopes). In this sense, the problem of the cosmological constant is a problem of naturalness, as this term is understood by specialists in particle physics and their colleagues: since the Universe in which we live contains so little dark energy compared to what we expect, our Universe is very unusual. and atypical.