
Hello! Last Saturday, we received the
Belyaev Prize for the publication of the scientific series
"New Science" . In honor of this, we have a 30% discount on this series, and the following is an excerpt from the book Shintan Yau and Steve Nadys “String Theory and Hidden Dimensions of the Universe” - “Loops in Space-Time”.
Sigmund Freud believed that in order to understand the nature of the human mind, it is necessary to study people whose behavior does not fit the generally accepted norms, that is, is anomalous, people obsessed with strange, obsessive ideas: for example, among his famous patients were “man - rat "(which had crazy fantasies, in which people who are dear to him are tied with a buttock to a pot of rats) and a" wolf-man "(who often had a dream, how white wolves sitting on a tree in front of his bedroom eat him alive). Freud believed that the most we learn about typical behavior, studying the most unusual, pathological cases. With the help of such studies, he said, we could eventually come to an understanding of both the norms and deviations from them.
We often use a similar approach in mathematics and physics. “We are looking for areas of space in which classical descriptions do not work, because it is in these areas that we discover something new,” explains Harvard astrophysicist Avi Löb. Whether we argue about abstract space in geometry or more material space, which we call the Universe, areas “where something awful happens to space, where things collapse”, as Loeb says, and these are areas that we call singularities.
Contrary to what you might think of singularities, they are widespread in nature. They are around us: a drop of water coming off and falling from a malfunctioning water tap is the most common example (often seen in my house), a place (well known to surfers) where ocean waves break and crush, newspaper folds (which are shown in the article important or just "water") or place twists on a balloon rolled into a French poodle. “Without singularities, you cannot talk about forms,” notes geometer Heisuke Hironaka, Professor Emeritus, Harvard University. He cites his own signature as an example: “If there are no intersecting lines, sharp corners, then this is just a scribble. A singularity would be intersecting or suddenly changing directions. There are many such things in the world, and they make the world more interesting. ”
In physics and cosmology, two types of singularities stand apart, among other innumerable possibilities. One view is a time singularity known as the Big Bang. I, as a geometer, do not know how to imagine the Big Bang, because no one, including physicists, really knows what it is. Even Alan Guth, the creator of the concept of cosmic inflation, a concept that he says “puts an explosion on the Big Bang,” admits that the term Big Bang has always suffered from uncertainty, probably because “we still don’t know (and may never know) what really happened. ” I believe that in this case modesty does not hurt us.
And although we are rather ignorant when it comes to applying geometry to the exact moment of the birth of the Universe, we, geometers, have achieved some success in fighting black holes. A black hole is essentially a section of space compressed to a point by gravity. All this mass, packed in tiny space, forms a superdense object, the second cosmic velocity (a measure of its gravitational attraction) near which exceeds the speed of light, which leads to the capture of any matter, including light.
Despite the fact that the existence of black holes stems from Einstein’s general theory of relativity, black holes still remain strange objects, and Einstein himself denied their existence until 1930, that is, 15 years after German physicist Karl Schwarzschild presented them as solutions famous Einstein equations. Schwarzschild did not believe in the physical reality of black holes, but today the existence of such objects is a recognized fact. “Currently, black holes are opened with surprising constancy every time someone from NASA needs another grant,” says Andrew Strominger.
And although astronomers have discovered a large number of black hole candidates and have accumulated a lot of observational data confirming this thesis, black holes are still shrouded in mystery.
The general theory of relativity gives a perfect and adequate description of large black holes, but the picture collapses when we move to the center of the vortex and consider a vanishingly small singular point of infinite curvature.
The general theory of relativity cannot fight tiny black holes that are smaller than a speck of dust — here quantum mechanics comes into play. The inadequacy of the general theory of relativity becomes evident in the case of such miniature black holes, when the masses are huge, the distances are tiny, and the curvature of space-time cannot be imaged. In this case, the theory of strings and Calabi – Yau spaces, which have been welcomed by physicists since the creation of the theory, helps, in particular, because they can resolve the conflict between supporters of the general theory of relativity and supporters of quantum mechanics.
One of the most heated debates between supporters of these outstanding branches of physics revolves around the issue of the destruction of information by a black hole. In 1997, Stephen Hawking from the University of Cambridge and Kip Thorn from Caltech made a bet with John Preskill, also from Caltech. The subject of the dispute was a consequence of Hawking’s theoretical discovery made in the early 1970s, namely, that black holes are not completely “black”. Hawking showed that these objects have a very low, but not zero temperature, which means that they must hold a certain amount of thermal energy. Like any other “hot” body, a black hole will radiate energy to the external environment until all the energy is completely exhausted and the black hole evaporates. If the radiation emitted by a black hole is strictly thermal and, therefore, is devoid of informational content, then the information originally stored within the black hole, say, if it absorbs a star with a certain composition, structure and history, it will disappear when the black hole will evaporate. This conclusion violates the fundamental principle of quantum theory, which states that the information of the system is always preserved. Hawking argued that, contrary to quantum mechanics, in the case of black holes, information could be destroyed, and Thorn agreed with him. Preskill defended the view that information would survive.
“We believe that if you throw two ice cubes into a pot of boiling water on Monday and check the water atoms on Tuesday, you will be able to determine that two ice cubes were thrown into the water the day before,” Strominger explains, “not practically, but basically". You can answer this question differently: take a book, for example “451 degrees Fahrenheit”, and throw it into the fire. “You may decide that the information is lost, but if you have enough instruments and computing equipment and you can measure all the parameters of the fire, analyze the ashes, and use the services of the“ Maxwell demon ”(or, in this case, the“ Laplace demon ”) you can reproduce the original state of the book, ”notes physicist Hiroshi Oguri from Caltech.6“ However, if you would throw the same book into a black hole, ”Hawking objected,“ then the data would be lost. ” Preskill, in turn, like Gerard 't Hooft and Leonard Süskind before him, upholds the position that the two cases are not radically different from each other and that the radiation of a black hole in some elusive way must contain information of the classic Ray Bradbury, which, theoretically, can be restored.
The stakes were high because one of the cornerstones of science — the principle of scientific determinism — was at stake. The idea of determinism is that if you have all the possible data describing a system in a specific period of time, and you know the laws of physics, then, in principle, you can determine what will happen to the system in the future, and also conclude what happened to her in the past. But if information can be lost or destroyed, the principle of determinism loses its force. You cannot predict the future, you cannot draw conclusions about the past. In other words, if the information is lost, then you are also lost. Thus, the scene was prepared for a decisive battle with the classics. “There was a moment of truth for string theory, which stated that it could appropriately reconcile quantum mechanics and gravity,” Strominger says. “But could she explain the Hawking paradox?” Strominger discussed this issue with Qumrun Wafa in a 1996 revolutionary article. To solve the problem, they used the concept of the entropy of a black hole. Entropy is a measure of the randomness or disorder of a system, but also serves as a characteristic of the amount of information contained in the system. For example, imagine a bedroom where there are many shelves, drawers and desks, as well as various works of art placed on the walls and hanging from the ceiling. Entropy is understood as the number of different ways in which you can organize or disorganize all your belongings — furniture, clothes, books, paintings, and various knick-knacks in this room. To a certain extent, the number of possible ways of organizing the same elements in a given space depends on the size of the room or its volume — the product of length, width, and height. The entropy of most systems is related to their volume. However, in the early 1970s, physicist Jacob Beckenstein, then a graduate student at Princeton, suggested that the entropy of a black hole is proportional to the area of the event horizon surrounding the black hole, rather than the volume enclosed within the horizon. The event horizon is often called the point of no return, and any object that crosses this invisible line in space will fall prey to gravitational attraction and will inevitably fall into a black hole. But it is probably better to talk about the surface of no return, since in reality the horizon is a two-dimensional surface, not a point. For a non-rotating (or “Schwarzschild”) black hole, the area of this surface depends solely on the mass of the black hole: the larger the mass, the larger the area. The statement that the entropy of a black hole — a reflection of all possible configurations of a given object — depends solely on the area of the event horizon, implied that all configurations are located on the surface and that all information about the black hole is also stored on the surface. (You can draw a parallel with the bedroom in our previous example, where all objects are located along the surfaces - walls, ceiling and floor, and do not float in the center of the room in the inner space.)
Beckenstein's work, along with Hawking's ideas about black hole radiation, gave the world an equation to calculate the entropy of a black hole. Entropy in accordance with the Beckenstein – Hawking formula is proportional to the area of the event horizon. Or, more precisely, the entropy of a black hole is proportional to the area of the horizon divided by four Newtonian gravitational constants (G). This formula shows that the black hole, which is three times more massive than the Sun, has a strikingly high entropy, about 1078 joules per degree Kelvin. In other words, the black hole is extremely disordered.
The fact that a black hole has such a staggeringly high entropy shocked scientists, given that in the general theory of relativity, a black hole is completely described by only three parameters: mass, charge and spin.
On the other hand, giant entropy implies a huge variability of the internal structure of a black hole, which should not be defined by three parameters.
The question arises: where did this variability come from? What other things inside a black hole can change just as much? The answer, apparently, lies in the division of a black hole into microscopic components, just as the Austrian physicist Ludwig Boltzmann did with gases in the 1870s. Boltzmann showed that the thermodynamic properties of gases can be derived from the properties of the constituent individual molecules. (There are actually a lot of these molecules, for example, in a single bottle of ideal gas under normal conditions there are approximately 1022 molecules.) Boltzmann's idea turned out to be remarkable for many reasons, including the fact that he came to it decades before the confirmation of the existence of molecules. Given the huge number of gas molecules, Boltzmann argued that the average speed, or average behavior of individual molecules, determine the general properties of a gas - volume, temperature and pressure, that is, the properties of the gas as a whole. Thus, Boltzmann formulated a more accurate picture of the system, stating that gas is not a solid body, but consists of many particles. A new look at the system allowed him to give a new definition of entropy as the statistical weight of a state — the number of possible microstates (ways) with which one can go into a given macroscopic state. Mathematically, this provision can be formulated as follows: entropy (S) is proportional to the natural logarithm of statistical weight. Or equivalently, the statistical weight is proportional to eS.
The approach that Boltzmann first applied is called statistical mechanics, and about a century later, people tried to interpret black holes using statistical mechanics. Twenty years after Beckenstein and Hawking set this task, it was still not solved. All that was needed to solve it was “the microscopic theory of black holes, the derivation of the laws of black holes from some fundamental principles - by analogy with the Boltzmann derivation of the thermodynamics of gases,” says Strominger. From the XIX century it was known that each system has entropy associated with it, and from the definition of Boltzmann's entropy it followed that the system's entropy depends on the number of microstates of the system components. “It would be a deep and distressing asymmetry if the relationship between entropy and the number of microstates were valid for any system in nature, with the exception of a black hole,” adds Strominger. Moreover, in accordance with Oguri, these microstates are “quantized”, because this is the only way to hopefully obtain a countable number of them. You can put a pencil on the table in an infinite number of ways, just as there are an infinite number of possible settings across the entire spectrum of electromagnetic radiation. But as we mentioned in the seventh chapter, radio frequencies are quantized in the sense that radio stations broadcast on a select number of discrete frequencies. The energy levels of the hydrogen atom are similarly quantized, so you cannot choose an arbitrary value; only certain energy values are allowed. “Part of the reason why Boltzmann was so hard to convince other scientists that his theory was right was that he was ahead of his time,” says Oguri. “Quantum mechanics was developed only after half a century.”
This was the problem that Strominger and Wafa undertook to solve. It was really a test of string theory, since the task involved quantum states of black holes, which Strominger called "the quintessence of gravitational objects." He felt that his duty was to solve this problem by calculating the entropy, or to admit that string theory was wrong.
The plan, which came up with Strominger and Wafa, was to calculate the entropy value using quantum microstates and compare it with the value calculated using the Beckenstein – Hawking formula, which was based on the general theory of relativity. Although the task was not new, Strominger and Wafa used new instruments to solve it, relying not only on string theory, but also on Joseph Polchinsky’s discovery of D-branes and the emergence of M-theory - both events took place in 1995, a year before their articles. “Polchinsky pointed out that D-branes carry the same type of charge as black holes, and have the same mass and tension, so they look and smell the same,” notes Harvard physicist He Ying. “But if you can use one to calculate the properties of the other, for example, entropy, then there’s something more than fleeting similarity.” This approach was chosen by Strominger and Wafa, using these D-branes to build new types of black holes, guided by string theory and M-theory.
The ability to build black holes from D-branes and strings (the latter are a one-dimensional version of D-branes) is the result of a “dual” description of D-branes. In models where the effectiveness of all forces acting on branes and strings (including gravity) is low (what is called a weak coupling), branes can be considered as thin, membrane-like objects that have a weak effect on the space-time around them and, therefore, a little like black holes. On the other hand, with a strong connection and a high interaction force, branes can become dense, massive objects with an event horizon and powerful gravitational influence — in other words, objects indistinguishable from black holes.
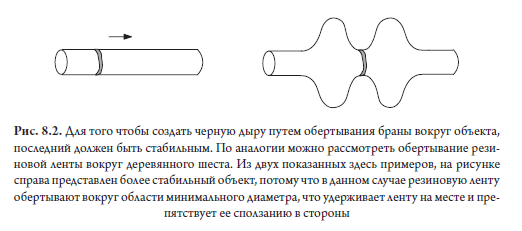
Nevertheless, more than a heavy bran or many heavy branes are required to create a black hole. You also need to somehow stabilize it, which is easiest to do, at least theoretically, by wrapping the brane around something stable that is not compressed. The problem is that an object that has a high tension (expressed as mass per unit length, area, or volume) can shrink to such a small size that it almost disappears, not having the appropriate structure to stop this process, just as ultra-tapping rubber tape is compressed into a tight lump if left on its own.
The key ingredient was supersymmetry, which, as mentioned in the sixth chapter, has the peculiarity of protecting the ground or vacuum state of the system from falling to lower and lower energy levels. Supersymmetry in string theory often implies Calabi – Yau manifolds, because such spaces automatically incorporate this feature. So the challenge is to find stable subsurfaces within Calabi – Yau varieties to wrap them in branes. These subsurfaces, or submanifolds that have a smaller dimension than the space itself, are sometimes called cycles (this concept has already been introduced in the book), which can sometimes be thought of as an incompressible loop around or through part of the Calabi – Yau variety. Technically speaking, a loop is a one-dimensional object, but the cycles include more dimensions, and they can be considered as non-compressing “loops” of a higher dimension.
Physicists tend to assume that the cycle depends only on the topology of the object or hole around which you can wrap, regardless of the geometry of this object or hole. “If you change the shape, the cycle will remain the same, but you will get a different submanifold,” explains Yin. He adds that since this is a property of topology, the cycle itself can do nothing with a black hole. “And only when you wind up one or more branes on a cycle, can you start talking about a black hole.” In order to ensure stability, the object with which you are wrapping - whether it is a bran, string or rubber band, must be tight, without any folds. The cycle around which you are wrapping should be the minimum possible length or area. Putting a rubber band around a uniform, cylindrical pole is not an example of a stable situation, because the tape can be easily moved from side to side. At the same time, if the pole has a different thickness, then stable cycles, which in this case are circles, can be found at points of the local minimum of the diameter of the pole, where the rubber band will not crawl from side to side.
To draw an analogy with the Calabi – Yau varieties, instead of a smooth pole, it is better to imagine another object that we wrap with a rubber band, for example, a grooved pole or a donut of variable thickness, on which the minimum cycles correspond to the places where the diameter has a local minimum. There are different types of cycles around which a brane can be wrapped inside Calabi – Yau varieties: these can be circles, spheres or tori of different dimensions, or high-genus Riemann surfaces. Since the branes carry mass and charge, the task is to calculate the number of ways to place them in stable configurations inside the Calabi – Yau manifold so that their resulting mass and charge are equal to the mass and charge of the black hole itself. “Although these branes are wrapped separately, they still stick together to the [Calabi – Yau] inner space and can be considered as parts of a larger black hole,” explains Yin. There is an analogy that, I admit, looks very unappetizing, but it was not I who invented it. , , , , - . , , , , . , , , . , — , . , D-, , , , .
, , : D- – ? , , : , , –? , , –. , , .
, , , , .
, 3- . , , , D-. . , , «»: , — , . , , , , . , . , .
, – . D- , . , , , , , . « , , , », — . , «, , ».
, . , D- , , , , D- . «, , , ? ? , , , , , ».16 , , , , . , 1996 , , . — , . , , -, . , — - — , , . , . « , –, — . — –».
, , , , . , , «, , », . , , , .
, 1996 , . –, , , — , , . . : « , . , “”. , , , , ».
, 1996 . – . , : , , ? 1997 , — , , (, –) -.
–, , «, , », , «, , , ». , – , , , , , — . , , « » . «» — , — , — , 1997 . , . 2004 , , 1996 , –, , , - . , , , .21 , , , « , , , »22. , : -, , , , , , , .
»
«New Science» 30% —