 Fig. one
Fig. oneThe nucleus of an atom is tiny, its radius is 10,000–100,000 times smaller than the entire atom. Each nucleus contains a certain number of protons (we denote it by Z) and a certain number of neutrons (we denote it by N), held together in the form of a ball, not much larger in size than the sum of their sizes. Note that protons and neutrons together are often called “nucleons”, and Z + N is often called A - the total number of nucleons in the nucleus. Also Z, "atomic number" is the number of electrons in an atom.
The typical cartoon image of the atom (Fig. 1) extremely exaggerates the size of the nucleus, but more or less correctly represents the nucleus as a carelessly connected accumulation of protons and neutrons.
Kernel content
How do we know what is in the core? These tiny objects are simply characterized (and this was just historically) due to the three facts of nature.
1. The proton and neutron differ in mass only by a thousandth part, so if we do not need extreme accuracy, we can say that all nucleons have the same mass, and call it the nucleon mass, m
nucleon :
m
proton ≈ m
neutron ≈ m
nucleon(≈ means "approximately equal to")
2. The amount of energy needed to hold together protons and neutrons in the nucleus is relatively small — about a thousandth of the mass energy (E = mc
2 ) of protons and neutrons, so the mass of the nucleus is almost equal to the sum of the masses of its nucleons:
M
nucleus ≈ (Z + N) × m
nucleon3. The mass of the electron is 1/1835 of the mass of the proton - so that almost the entire mass of the atom is contained in its nucleus:
M
atom ≈ M
nucleusThis implies the presence of the fourth important fact: all the atoms of a certain isotope of a certain element are the same, as are all their electrons, protons and neutrons.
Since the most common isotope of hydrogen contains one electron and one proton:
M
hydrogen ≈ m
proton ≈ m
nucleonthe mass of the atom M is
an atom of a certain isotope simply equal to Z + N multiplied by the mass of the atom of hydrogen
M
atom ≈ M
nucleus ≈ (Z + N) × m
nucleon ≈ (Z + N) × M
hydrogenand the error of these equations is approximately 0.1%.
Since neutrons are electrically neutral, the electric charge Q of the
nucleus of the nucleus is simply equal to the number of protons multiplied by the electric charge of the proton ("e"):
Q
nucleus = Z × Q
proton = Z × e
Unlike the previous equations, this equation holds exactly.
Summing up:
Z = Q
core / e
A = Z + N ≈ M
atom / M
hydrogenThese equations are illustrated in Fig. 2
 Fig. 2
Fig. 2Using the discoveries of the last decades of the XIX century and the first decades of the XX, physicists knew how to measure both the red values in the experiment: the nuclear charge in e, and the mass of any atom in the hydrogen atoms. So these values were already known in the 1910s. However, they could be correctly interpreted only in 1932, when James Chadwick determined that the neutron (the idea of which Ernest Rutherford suggested in 1920) is a separate particle. But as soon as it became clear that neutrons exist, and that their mass is almost equal to the mass of a proton, it immediately became clear how to interpret the numbers Z and N — the number of protons and neutrons. And also a new mystery was born immediately - why protons and neutrons have almost the same mass.
To be honest, physicists of that time were scientifically lucky that it was all so easy to install. The laws of masses and charges are so simple that even the longest riddles were discovered immediately after the discovery of a neutron. If even one of the facts of nature I have listed were wrong, then it would take much longer to understand what is happening inside the atoms and their nuclei.
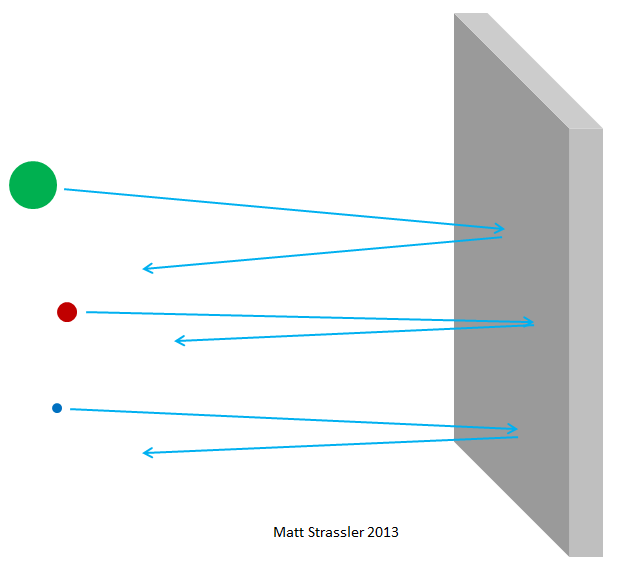 Fig. 3
Fig. 3Unfortunately, from other points of view it would be much better if everything turned out to be more complicated. It was hardly possible to find the worst moment for this scientific breakthrough. The discovery of the neutron and understanding of the structure of the atom coincided with the world economic crisis, known as the Great Depression, and with the emergence of several authoritarian and expansionist governments in Europe and Asia. The race began quickly leading scientific powers in the field of understanding and obtaining energy and weapons from the atomic nucleus. Reactors producing nuclear energy were obtained in just ten years, and in thirteen nuclear weapons. And today we have to live with the consequences of this.
How do we know that the nucleus of an atom is small?
One thing is to convince yourself that a particular nucleus of a certain isotope contains Z protons and N neutrons; the other is to convince oneself that the nuclei of atoms are tiny, and that the protons with neutrons, being squeezed together, do not smear into porridge and do not dissolve into the mash, but retain their structure, as the cartoon image suggests. How can this be confirmed?
I already mentioned that atoms are practically empty. It is easy to check. Imagine aluminum foil; nothing is visible through it. Since it is opaque, you can decide that the atoms of aluminum:
1. So large that there is no gap between them
2. So dense and solid that the light does not pass through them.
As for the first point, you will be right; in solid matter between two atoms there is almost no free space. This can be observed in the images of atoms obtained using special microscopes; atoms look like small spheres (whose edges are the edges of electron clouds), and they are pretty tightly packed. But with the second point you will be mistaken.
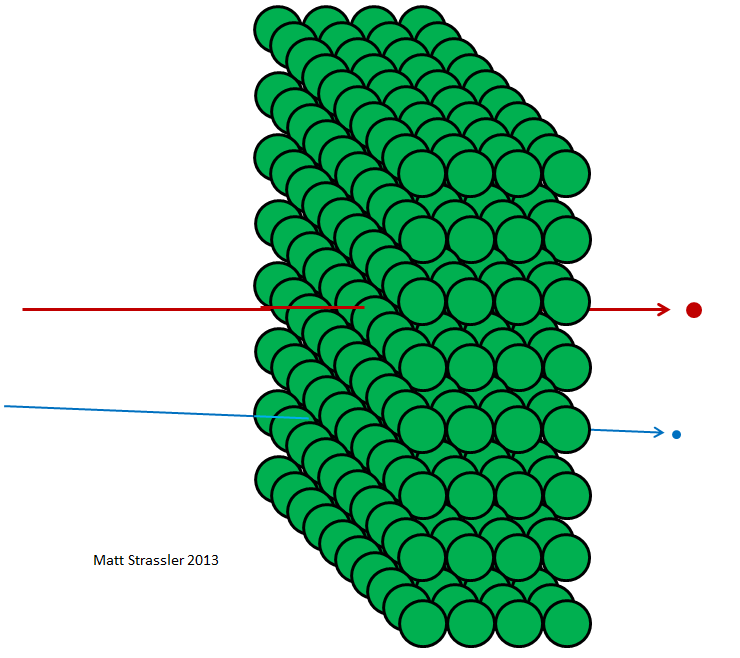 Fig. four
Fig. fourIf atoms were impenetrable, then nothing could pass through aluminum foil — neither photons of visible light, nor x-ray photons, nor electrons, nor protons, or atomic nuclei. All that you would have directed towards the foil would either get stuck in it or bounce off - just like any thrown object should bounce or get stuck in a plasterboard wall (Fig. 3). But in fact, high-energy electrons can easily pass through a piece of aluminum foil, like x-ray photons, high-energy protons, high-energy neutrons, high-energy nuclei, and so on. Electrons and other particles - almost all, more precisely - can pass through the material without losing either energy or momentum in collisions with anything contained inside the atoms. Only a small part of them will hit the atomic nucleus or electron, in which case they may lose most of their initial energy of motion. But most of the electrons, protons, neutrons, x-rays and all that kind of thing just pass easily through (fig. 4). This is not like throwing pebbles into a wall; this is like throwing pebbles into a mesh fence (fig. 5).
 Fig. five
Fig. fiveThe thicker the foil - for example, if you put more and more sheets of foil together - the more likely the particles launched into it, collide with something, lose energy, bounce off, change direction or even stop. The same would be true if you layered one after another wire mesh (Fig. 6). And, as you understand, from how far an average pebble can penetrate the layers of the grid and how large the gaps in the grid are, scientists can calculate, based on the distance traveled by electrons or atomic nuclei, how empty the atom is.
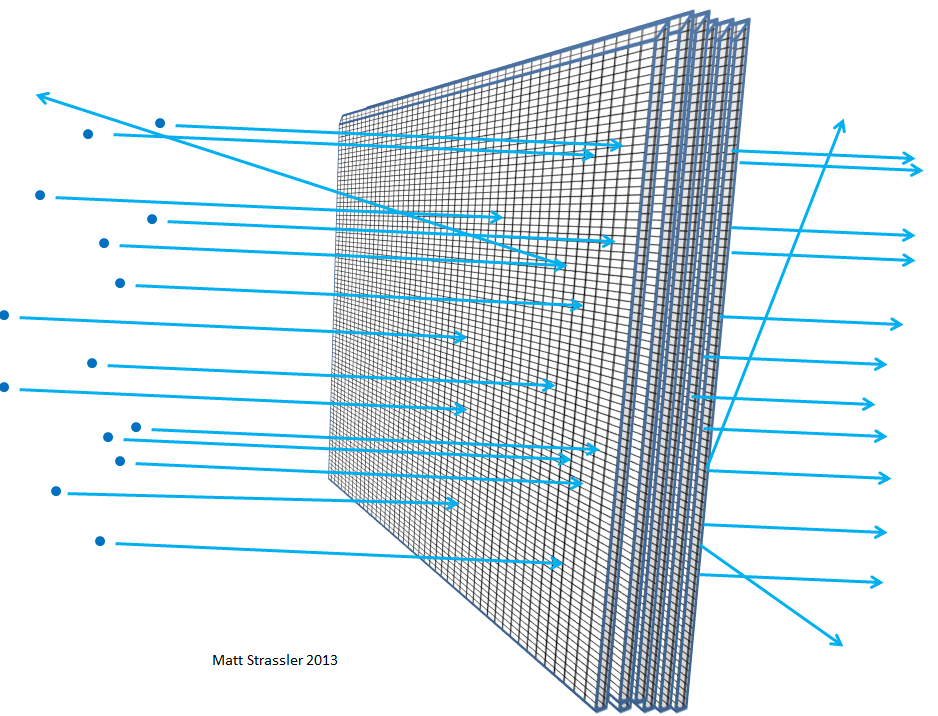 Fig. 6
Fig. 6Through such experiments, physicists at the beginning of the 20th century found that nothing inside the atom — neither the atomic nucleus nor the electrons — can be greater than one-thousandth millionths of a meter, that is, 100,000 times smaller than the atom itself. The fact that the nucleus reaches this size, and the electrons are at least 1000 times smaller, we establish in other experiments, for example, in the scattering of high-energy electrons from one another, or from positrons.
To be even more accurate, it should be mentioned that some particles will lose some of the energy in the process of ionization, in which the electrical forces acting between the flying particle and the electron can pull an electron out of an atom. This is a long-range effect, and the collision is not really. The total energy loss is significant for flying electrons, but not for the flying nucleus.
You may wonder if the way particles go through the foil is similar to how a bullet goes through the paper - pushing the pieces of paper to the sides. Perhaps the first few particles just push the atoms apart, leaving large holes that the next ones pass through? We know that this is not the case, since we can conduct an experiment in which particles pass inside and outside of a container made of metal or glass, inside which there is a vacuum. If the particle, passing through the walls of the container, created holes larger than atoms, then air molecules would rush inside and the vacuum would disappear. But in such experiments, the vacuum remains!
It is also quite easy to determine that the nucleus is not a particularly structured pile, within which the nucleons retain their structure. This is already possible to guess from the fact that the mass of the nucleus is very close to the sum of the masses of the protons and neutrons contained in it. This is done for atoms and molecules — their masses are almost equal to the sum of the masses of their contents, except for a small correction for the binding energy — and this is reflected in the fact that the molecules are fairly easy to break up into atoms (for example, heating them so that they collided more strongly with each other), and knock electrons out of atoms (again, by heating). In a similar way, it is relatively easy to break the nucleus apart, and this process will be called fission, or it will be possible to assemble a nucleus from smaller nuclei and nucleons, and this process will be called fusion. For example, relatively slow-moving protons or small nuclei colliding with a larger nucleus can break it apart; it is not necessary that the colliding particles move at the speed of light.
 Fig. 7
Fig. 7But in order to understand that this is not inevitable, I will mention that protons and neutrons themselves do not have these properties. The mass of a proton does not equal the approximate sum of the masses of the objects contained in it; a proton cannot be broken apart; but in order for the proton to demonstrate something interesting, energy is needed that is comparable to the energy of the mass of the proton itself. Molecules, atoms and nuclei are relatively simple; protons and neutrons are extremely complex.