After the publication of my
article about what the Earth would be like if it were twice as large, the readers had a question: “What about the toroidal Earth”? The question is not the most original, this topic has already been
discussed online and carried out its
modeling . But I love to do everything myself, so I tried to conduct my own analysis.
Can there be a toroidal planet?
The stability of the toroidal planet is not obvious. From a practical point of view, planets can be viewed as liquid balls without surface tension — the strength of a stone cannot be compared with the weight of a planet. They have equipotential gravity surfaces with regard to the centrifugal potential. If this were not so, then there would be places on them that could reduce their energy by flowing to a lower potential. Another obvious fact is the existence of an upper limit of the rotational speed, after which the planet collapses: the centrifugal force at the equator exceeds gravity and the material flies into space.
The equilibrium forms of rotating ellipsoid planets, held by the force of their own gravity, were
comprehensively analyzed . It all began with Newton, at the same time early heroic expeditions were conducted to establish the shape of the Earth,
Maclauren continued his work,
Jacobi discovered that at high speeds of rotation, ellipsoids with unequal axes turn out to be more stable than the flattened Macloraine ellipsoids.
Subramanian Chandrasekar conducted
interesting developments in this area. But since then computers have appeared, and therefore, analytical and numerical calculations of
more complex or
relativistic cases have been carried out.
Equilibrium forms of rotating toroids were analyzed in the same way - this was done by
Poincaré ,
Sofia Kovalevskaya , and
Frank Dyson (
Dyson 1893 ,
Dyson 1893b ). At least
in theory, it is possible to unwind the ellipsoidal planet to the state of a ring, although there are many possibilities for oscillations that destabilize the system, after which a leap into a ring state occurs.
The ring can be unstable, in particular, due to “nodal” instability - an increasing amount of mass can accumulate in certain meridians, as a result of which a break will occur into several separate masses. Dyson analyzed this case and found that it matters when R (the distance from the center of the torus to the center of the pipe) is more than three times the radius of the pipe (radius of the pipe) —that is, the thin hoops are unstable. There is also a lower rotational speed at which the ring becomes unstable and tidal forces
compress it into an ellipsoid . So the total mass and angular momentum must be correctly set from the very beginning.
Apparently, the laws of physics do not prohibit the emergence of toroidal planets. Just the probability of their occurrence is extremely small, and such a planet is likely to be unstable on geological time scales due to external disturbances. So, if we assume that it already exists, perhaps because of the actions of an advanced civilization, the aesthetics of which are stronger than reason - what will be its characteristics?
Directions
We will call two circles parallel to the plane of rotation equators (external and internal). In the case when there will be no fundamental difference between them for the topic under discussion, I will call them just the equator. The poles will be the circles furthest from the equatorial plane.
The direction to the center will indicate the direction to the axis of rotation, to the rim - from the axis of rotation. To the plane - towards the equatorial plane. North - in the direction of the nearest part of the north pole circle, south - in the direction of the nearest part of the south pole circle.
Toroid gravity
How does gravity work on a toroidal planet?
In the case of a very large R, the toroidal planet, in essence, becomes cylindrical. In this case, gravity decreases as 1 / r, where r is the distance from the axis. The impact on any section will be proportional to the total mass (proportional to R) and gravity (proportional to 1 / R), so that the total force will remain constant with increasing R. It will balance a certain rotation. Surface gravity 2G rho / r, where rho is the mass per unit length. So as long as the surface gravity is large enough (with small r), this force will overcome the centrifugal acceleration and nothing will fly away. But for a torus with a small radius, everything is much more complicated.
I decided to use the Monte Carlo method to estimate the equilibrium form. Starting with the total mass of the planet and the angular momentum, I distributed a multitude of massive, infinitely thin rings (the potential I took from this
exercise is good that in classical physics the electric and gravitational potential are the same). I calculated their total potential and added centrifugal. This allows one to approximate equipotential surfaces and to “fill” the potential closer to the center of the torus with more and more rings until their mass corresponds to the mass of the planet. I recalculated the angular velocity based on the new mass distribution. Then he repeated the process until either the planet scatters, or shrinks into a ball, or a lot of iterations take place. This is not the most elegant method (decomposition in a series of toroidal harmonics is used in the literature), but it was enough for me.
The main result - a toroidal planet realistically allows for a fairly large mass and angular momentum. The section is neither round nor elliptical, but resembles an egg, with a slightly sharper inner curvature than the outside.
Why the planet does not flatten into a disk? Rotation is trying to flatten the planet, but he has to work against local gravity, which is trying to squeeze it into a ball (or cylinder).
Although in my simulation such planets turned out to be stable, the spread of permissible values was low: most of the combinations of mass and angular momentum were unstable. I have not analyzed the complex issue of nodal instability.
I will consider here a plump toroid with a mass equal to the mass of the Earth and a small central hole ("Donut"), as well as a wider, hoop-like toroid with a mass of 6 terrestrial, but more close to earth gravity ("Hoop").
Donut
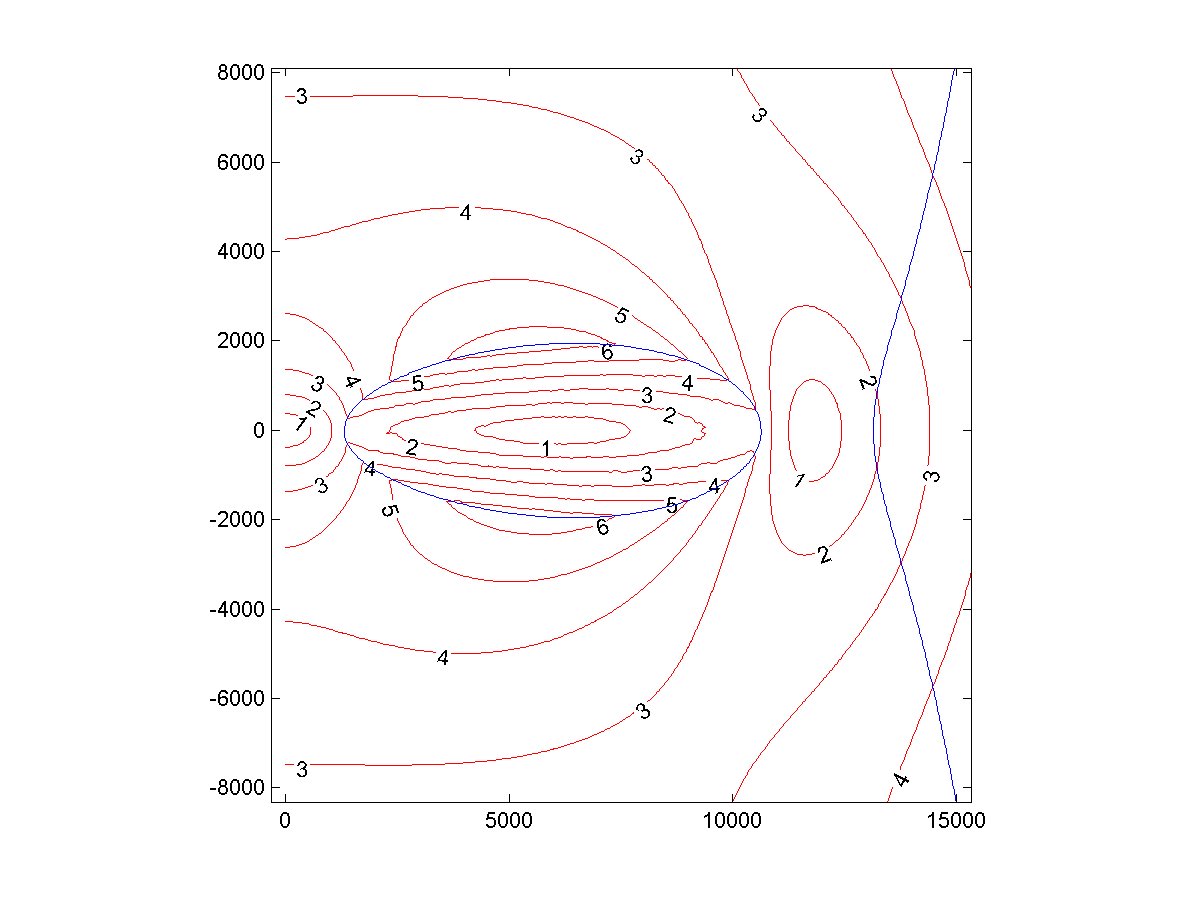 Fig. 1: local gravitational acceleration (m / s 2 ) around the Donut, experienced by an object rotating together with it
Fig. 1: local gravitational acceleration (m / s 2 ) around the Donut, experienced by an object rotating together with itThe inner equator of the Ponchik is 1305 km from the center, and the outer equator is 10663 km. The diameter of the equator - 9328 km.
The planet extends a distance of 1953 from the equatorial plane, and the diameter from north to south is 3906 km. The diameter ratio is 2.4.
The circumference from north to south is 21587 km (0.54 terrestrial), and from west to east - 66809 km (1.7 terrestrial). The total area is 8.2 x 10
8 km
2 (1.6 terrestrial). Total volume = 1.1 x 10
12 km
3 , differs from the earth no more than by 1% (after all, Donut was chosen as a planet of the earth’s mass). The ratio of volume to area - 1300, 61% of Earth - per unit volume of area more.
The day lasts 2.84 hours.
Hoop

Fig. 2: local gravitational acceleration (m / s
2 ) around the Hoop, experienced by an object rotating together with it
The inner equator of the Hoop is 8633 km from the center, and the outer one is at 19937 km. The diameter of the equator 11304 km.
The planet extends from the equatorial plane to 4070 km, the diameter from north to south is 8141 km. The aspect ratio of the cross section is approximately equal to 4: 3, as with older monitors. The radius of the circle of the center of mass is 14,294 km.
The circumference from north to south is 30,794 km (0.77 Earth), and from west to east - 125270 (3.1 Earth). The total area is 2.5 x 10
9 km
2 , 4.9 times the size of the earth, and the total volume is 6.5 x 10
12 km
3 , 6 times the size of the earth. The ratio of volume to area = 150, 70% of the earth.
The day lasts 3.53 hours.
Environment
What is life like on a toroidal earth?
Gravity
Surface gravity depends on location. It is the weakest along the inner and outer equators, and the strongest is near the poles, a little towards the center. This is one of the main differences.
Donut
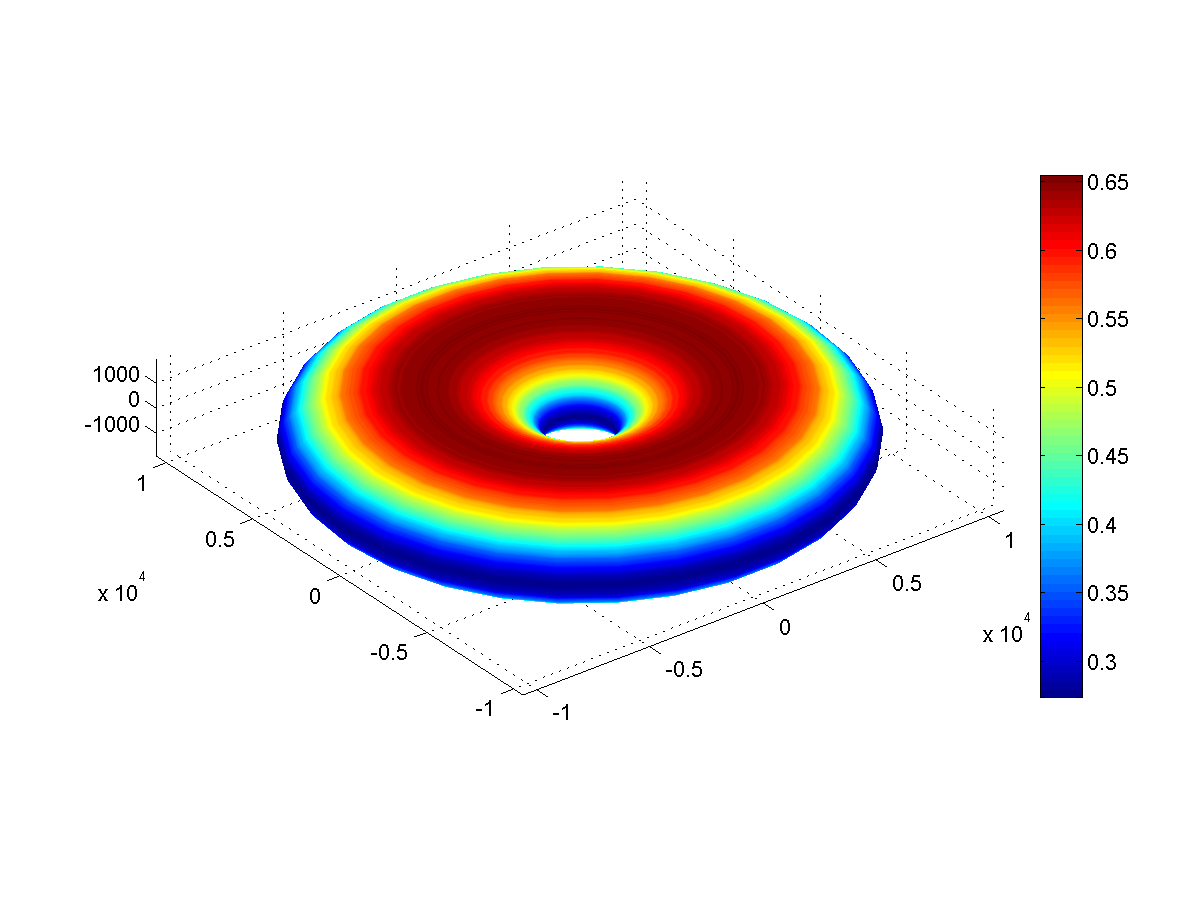 Fig. 3: gravity on the donut surface (m / s 2 )
Fig. 3: gravity on the donut surface (m / s 2 )On Ponchik, gravity along the equators is only 0.3 G, and 0.65 G along the poles. The speed of escape is not too different from Earth, and is equal to 11.4 km / s.
The geosynchronous orbit around Ponchik is very close to the external equator, less than 2000 km. The satellite flying over it will remain above one place, but, unlike the Earth, it will not be able to cover the whole hemisphere with its gears, only a small region.
On the other hand, the peripheral speed at the equator is 6.5 km / s, and the launches are easier. A rocket launched to the east requires a speed of just 4.9 km / s in order to escape.
In the middle of the hole there is an unstable Lagrange point. The satellite there will be attracted to the equatorial plane, but any deviation from it will increase.
Hoop
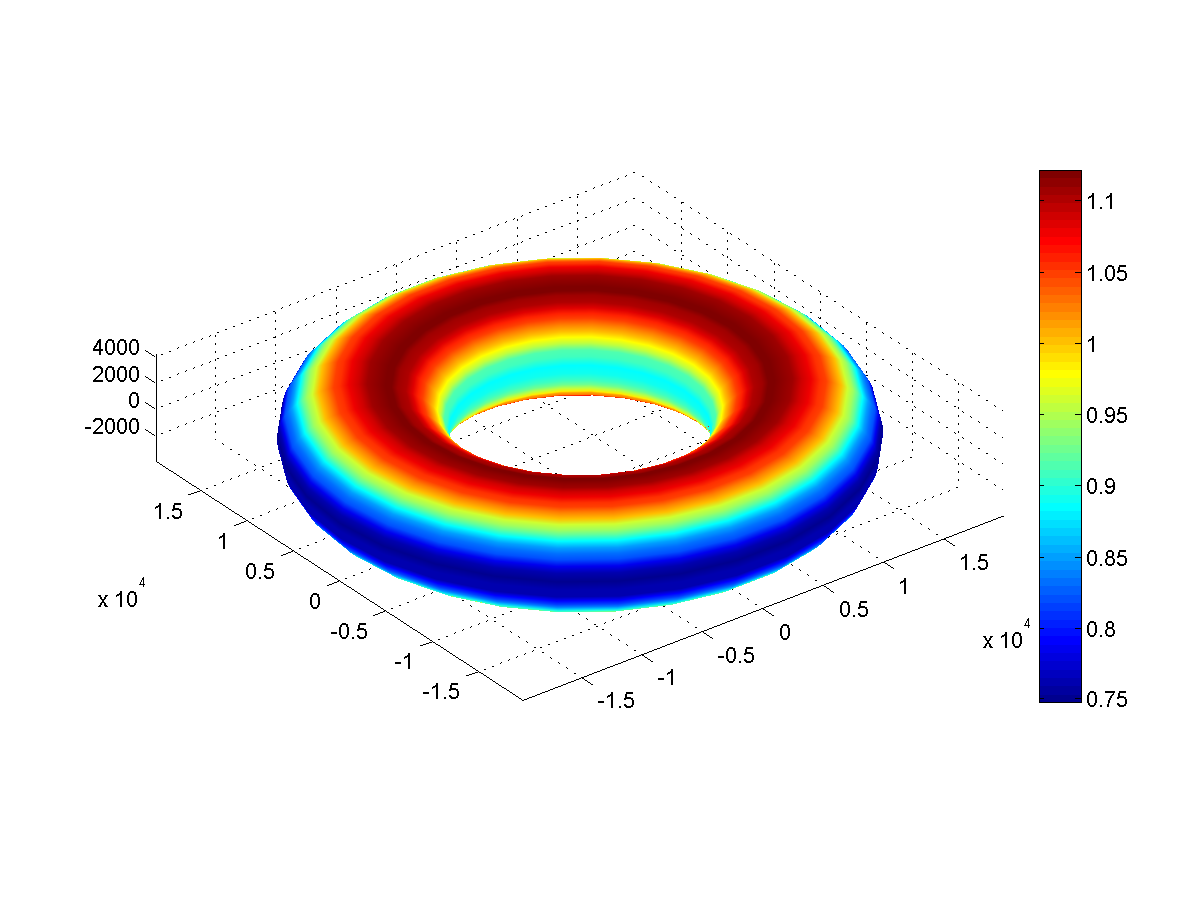 Fig. 4: surface gravity (m / s 2 ) Hoop
Fig. 4: surface gravity (m / s 2 ) HoopAt the Hoop, gravity along the poles is 1.1 G, and along the outer equator - just 0.75 G. At the inner equator, it is slightly larger, about 0.81 G.
The speed of escape is 19 km / s (remember, the planet weighs 6 times more than the Earth). At the outer equator, the escape velocity is 9.9 km / s - a rocket launched to the east will need to be given a speed of 10 km / s.
Once again, low gravity at the equator and high at the poles does not mean that things will roll or creep to the poles: as already mentioned, the surface will be equipotential, so gravity, along with centrifugal correction, will always be perpendicular to it.
Air masses flowing to the poles will flatten. The difference in gravity will create a horizontal pressure difference, which will, in conjunction with the temperature difference, create non-trivial flows.
Shine
Nights and days on such worlds will be very short. The environment will not have time to cool or warm during daily cycles. What matters is the difference in the amount of light produced during longer periods, that is, seasons. If these worlds move in an orbit similar to that of the earth, around a sun-like star, it will matter.
If the orbit is smaller, tidal forces will soon make these planets unstable. Since the brightness of the star grows approximately as the fourth degree of its mass, and the radius of the residential zone grows as the square root of brightness, in the residential zone the scale of tidal forces will be equal to M / (√ (M
4 ))
3 = 1 / M
5 . That is, bright stars will have much less tidal effects - perhaps Donut and Hoop better rotate around a white-blue F-class star, rather than around a G-class star, like our Sun, just in case.
The outer part of the toroidal planet is not too different from the surface of the normal ellipsoid. The day comes when the sun rises over the eastern horizon, and sunset occurs over the western. The sun passes in a large circle, slowly moving from north to south and back throughout the year, which ensures the presence of seasons. However, on the inner side of the planet everything is different. Other parts of the planet may cover the sun - in the first approximation, you can expect less energy.
We can consider three different cases: zero axis tilt, 23 degrees (like that of the Earth) and 45 degrees.
Zero slope
At zero slope, the inner side of the sun will not see: it will always be hidden behind the horizon or beyond the world arch. At the poles the sun moves along the horizon, and a little closer to the center there will always be dusk. Temperature differences will be large, the inner part of the planet will be subject to subarctic temperatures - this is not much different from the world with
synchronous rotation , and in principle in these places water (and possibly carbon dioxide) should always be condensed. As a result, at the outer equator there should be arid (perhaps not too hot places), possibly inhabited twilight circumpolar regions, and an icy inner part.
23 degree slope
 Fig. 5: Seasons on Ponchik in spring, summer, autumn and winter
Fig. 5: Seasons on Ponchik in spring, summer, autumn and winterFor a slope of 23 degrees, coinciding with the earth, spring and autumn will coincide with zero slope - light along the equator and dark inside, near the hole. In the summer and winter, the sun will have a chance to penetrate the rim, on the opposite side of the hole. There will also be large areas with the sun at midnight or with eternal night in summer or winter. On Earth, the polar regions are small, but here they will be long continuous circles.
Spring sunrises and autumnal twilight on the inside should give amazing deep colors, as the sun will rise through the atmosphere on the other side of the planet (pre-ascended or setting, so to speak). All this, together with local atmospheric optical effects will give very deep reds and gradients. Immediately before or after sunset or dawn, parts of the solar corona will be visible.
This spectacle would have been more impressive if it had not been so short. On Earth, the sun passes about 15 ° per hour. In the fastest case, the sun passes one of its diameter in 2.1 minutes. On the Ponchik, the sun will pass 127 ° per hour, and on the Hoop - 102 °. Sunrise and sunset will take 15 or 19 seconds, respectively. Inclined angle and atmospheric delays will prolong the spectacle a little, but for the inhabitant of the earth it will be too short.
If you stand on the inside of the surface and look up, the other side will occupy 20 degrees of the sky on the Hoop and 30 degrees on the Donut - a huge arch across the sky.
Why is the Donut not much wider? It is very flat, so it looks shortened in the sky. This, by the way, means that during the refraction of sunlight through the atmosphere of the other side, at sunrise or sunset, the red colors will be much deeper than on the Hoop.
Inside, the illuminated opposite part of the torus will illuminate everything in the manner of moonlight. But the surface area will be larger, so the nights will be much brighter. At the Hoop, the light will be 16,000 times stronger than the Earthly (8000 lux), when the entire opposite part is lit (we will take the albedo equal to the Earthly), and the night will be similar to a cloudy day. On the Donut, the lighting will reach a dim day (12,000 lux). But this is the situation of the fully illuminated opposite side - during the equinox only a thin strip will be visible.
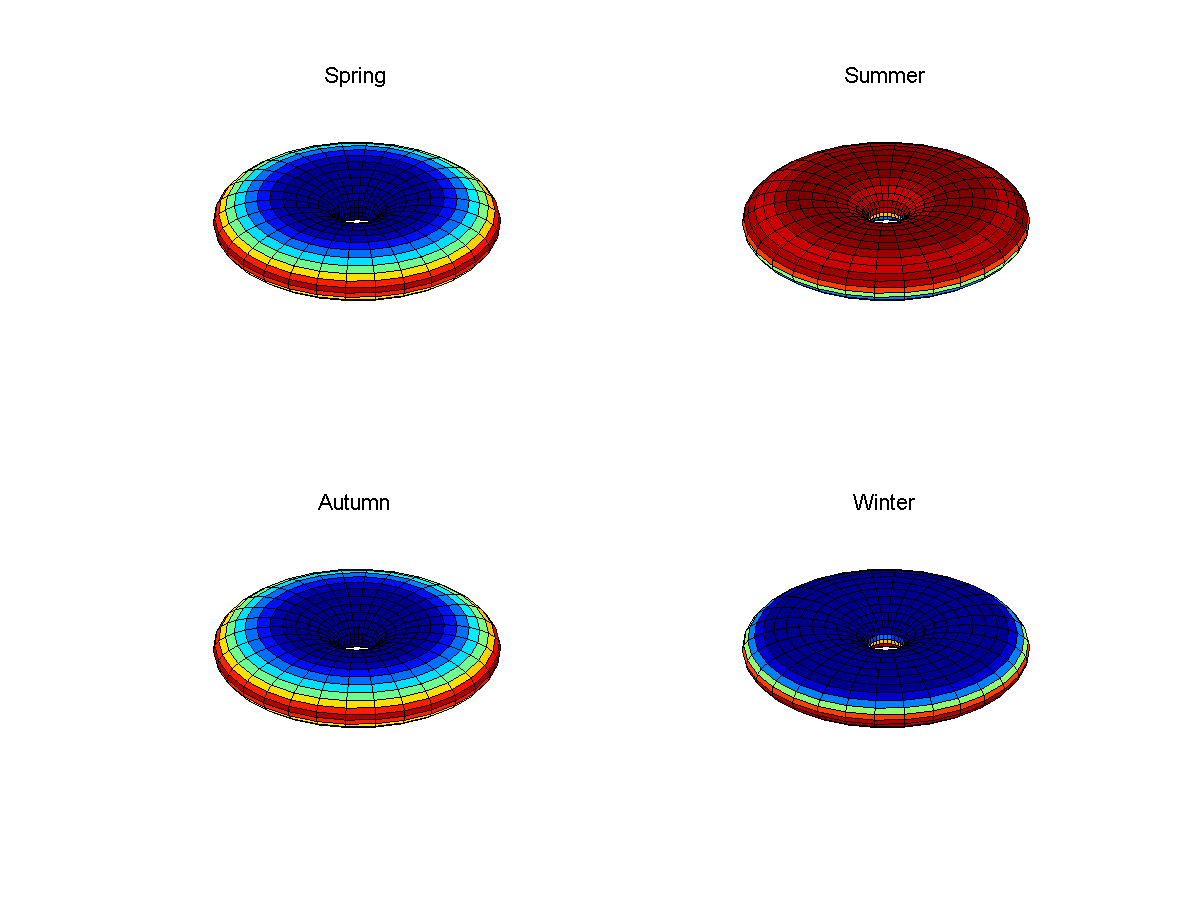 Fig. 6: the average illumination per day on the Donut during spring, summer, autumn and winter for a case with a slope of 23 degrees
Fig. 6: the average illumination per day on the Donut during spring, summer, autumn and winter for a case with a slope of 23 degreesIn the case of Ponchik, a rather flat surface means that the northern or southern hemisphere (hemispheric) will get a lot of sunlight. The total warming up of the planet will be large during these seasons than during spring and autumn, unlike Earth, where it is constant, as the area receiving light remains constant. Nontrivial effects due to angles between the surface and sunlight will also be observed, and temperate zones will receive slightly less energy than the polar regions and the tropics.
On the outer tropics there will be approximately the same influx of solar energy. Towards the poles, seasonality is felt stronger: the tropics receive more energy in summer than the equator at any time. Winters will be just as dark. At the poles and behind them, on the inside in places with maximum gravity, the sun will be visible for half a year, and then there will be a polar night. Here the climate will change dramatically - at least in the outer tropics there will be 1.5 hours nights, and here they will last for 6 months. Finally, closer to the inner equator next to the hole, day and night will be equal in winter (and the light reflected by the other side will also be added), so the temperature will be slightly higher.
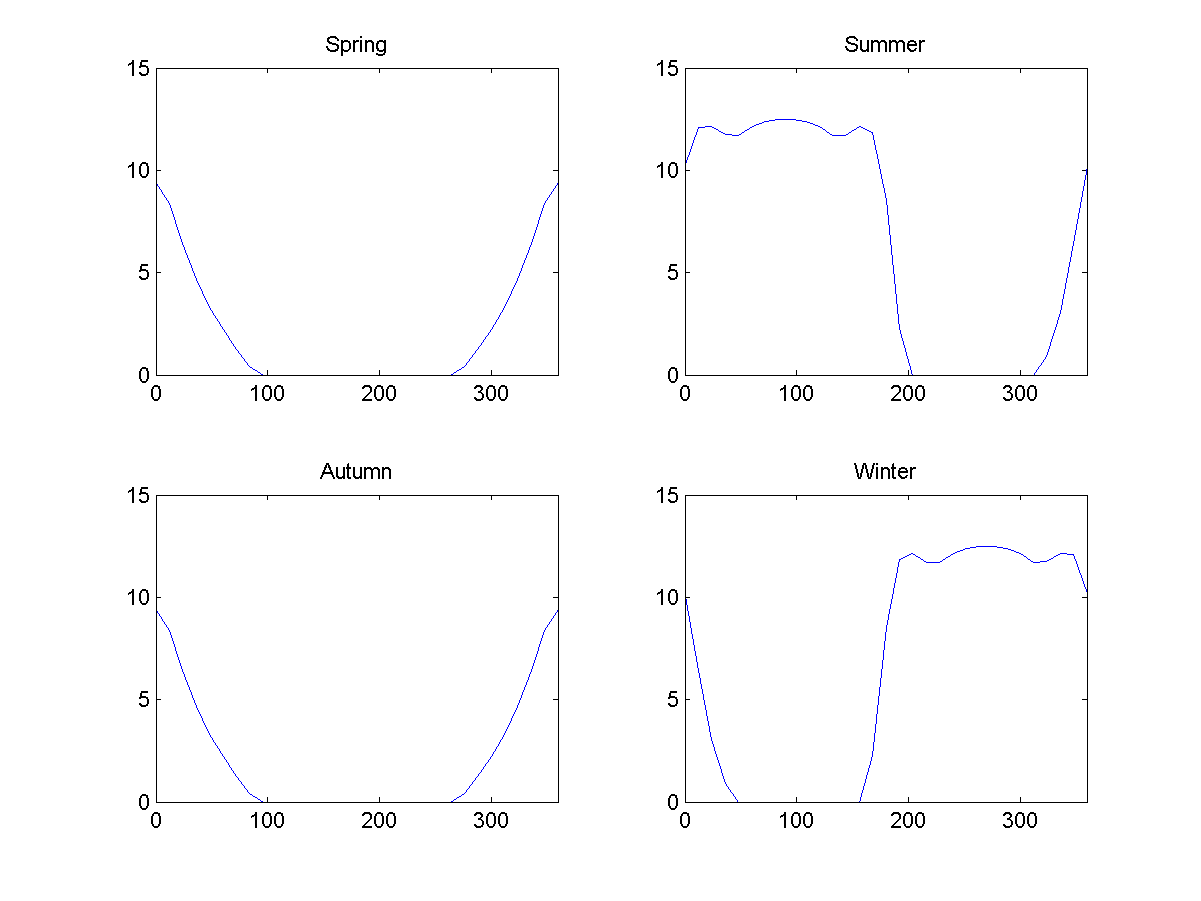 Fig. 7: Average illumination during different seasons on Ponchik, as a function of latitude in the case of 23 degrees. 0 means the outer equator, 90 - the north pole, 180 - the inner equator, 270 - the south pole.
Fig. 7: Average illumination during different seasons on Ponchik, as a function of latitude in the case of 23 degrees. 0 means the outer equator, 90 - the north pole, 180 - the inner equator, 270 - the south pole.A big difference in the amount of energy received on the sunny summer side of the hole and on the dark winter side of the hole will lead to the emergence of severe weather - but due to other oddities of these worlds, it will be harder to balance energy differences than on Earth.
On average, the equatorial exterior will receive 2.5 times more energy than the polar parts, and the interior will receive four times less energy than the surrounding areas.
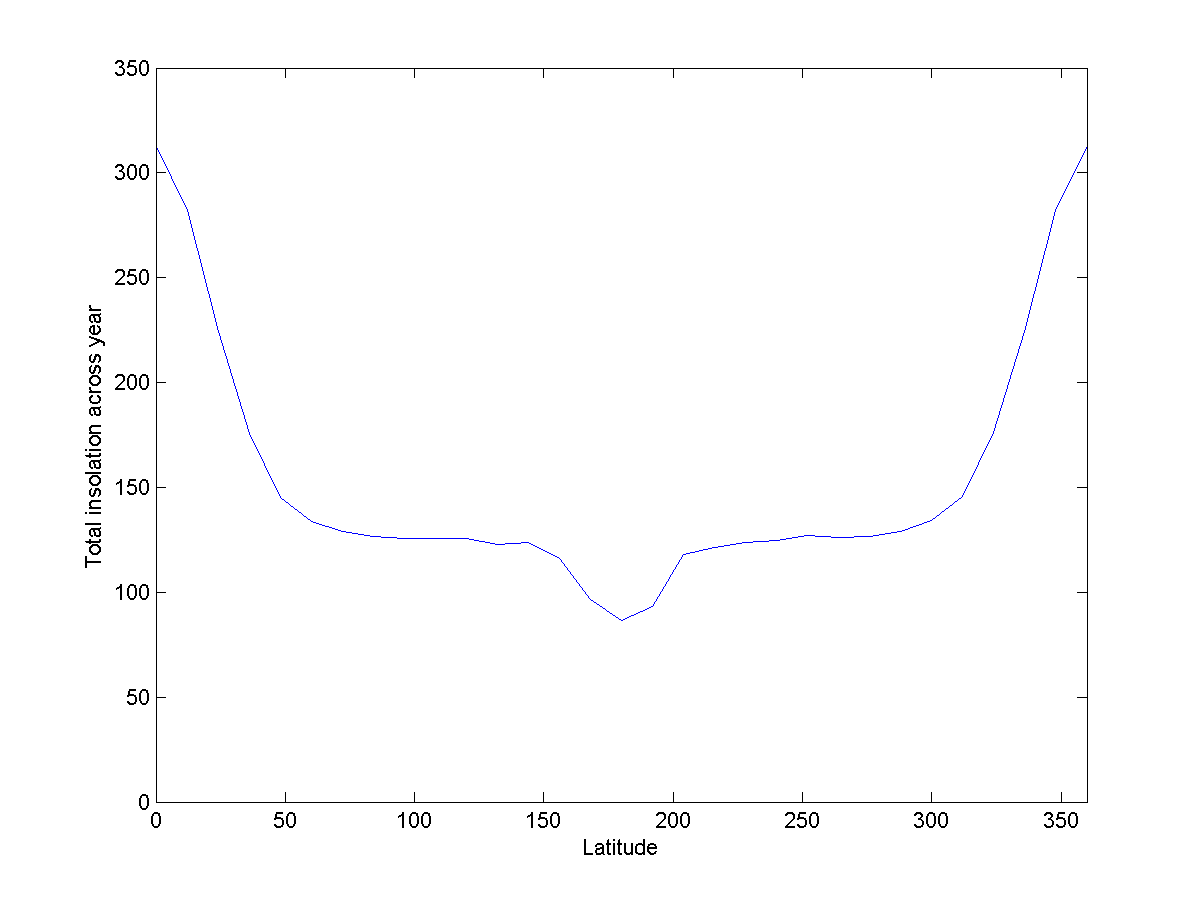 Fig. 8: energy at different latitudes of the Donut
Fig. 8: energy at different latitudes of the DonutA hoop casts less shadow on itself. More importantly, it is not as flat as Donut.
 Fig. 9: average coverage during the day on the Hoop, 23 degrees
Fig. 9: average coverage during the day on the Hoop, 23 degrees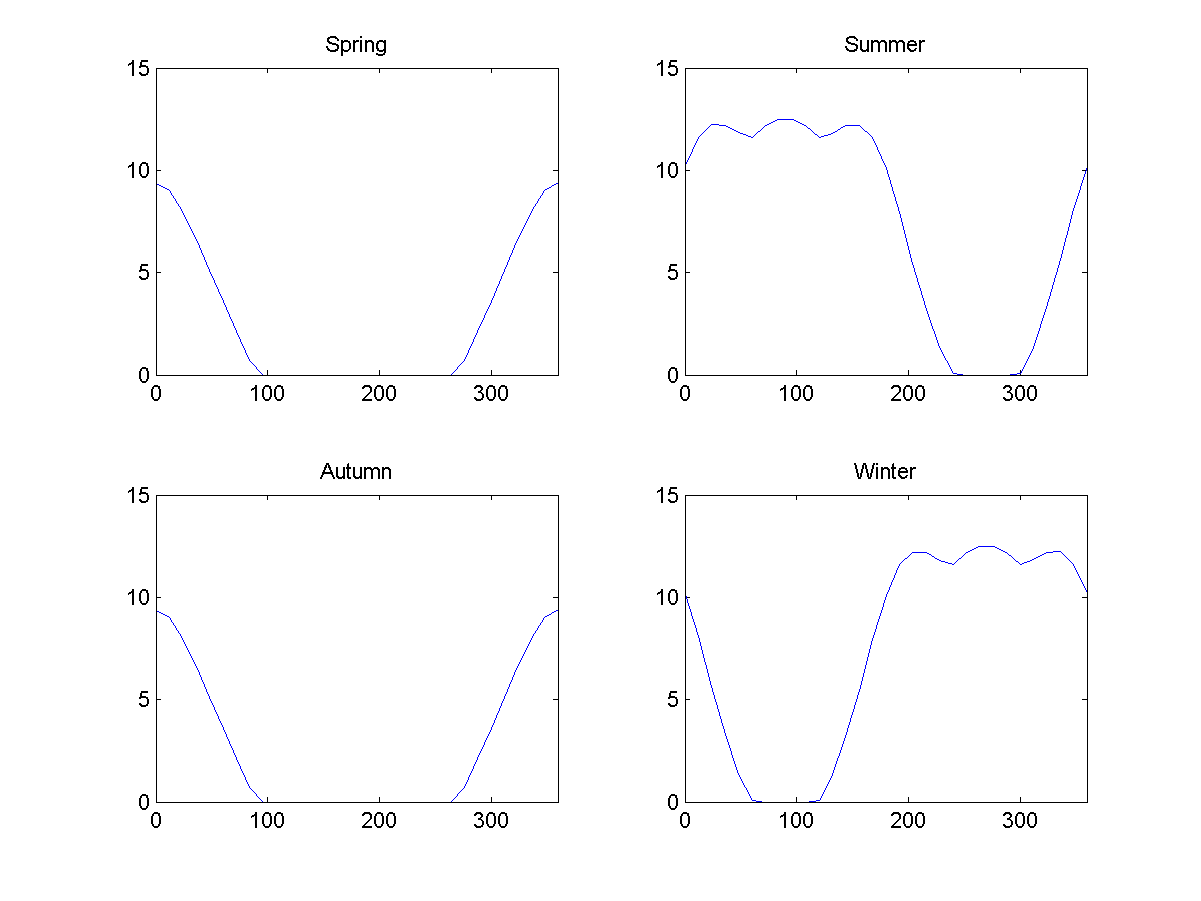 Fig. 10: Average illumination during different seasons on the Hoop, as a function of latitude in the case of 23 degrees. 0 means the outer equator, 90 - the north pole, 180 - the inner equator, 270 - the south pole.
Fig. 10: Average illumination during different seasons on the Hoop, as a function of latitude in the case of 23 degrees. 0 means the outer equator, 90 - the north pole, 180 - the inner equator, 270 - the south pole.At first glance, the seasons look expected. In spring and autumn, the inner parts will be hidden in the shade, in summer and in winter one polar region is more lighted, and the other is weaker, and the inner parts will get their light. This will lead to the presence of a seasonal cycle in the inner part of the planet, going two times faster than on the outside (it will be the same as on the Donut): the warm weather will be in “July” and in “January”.
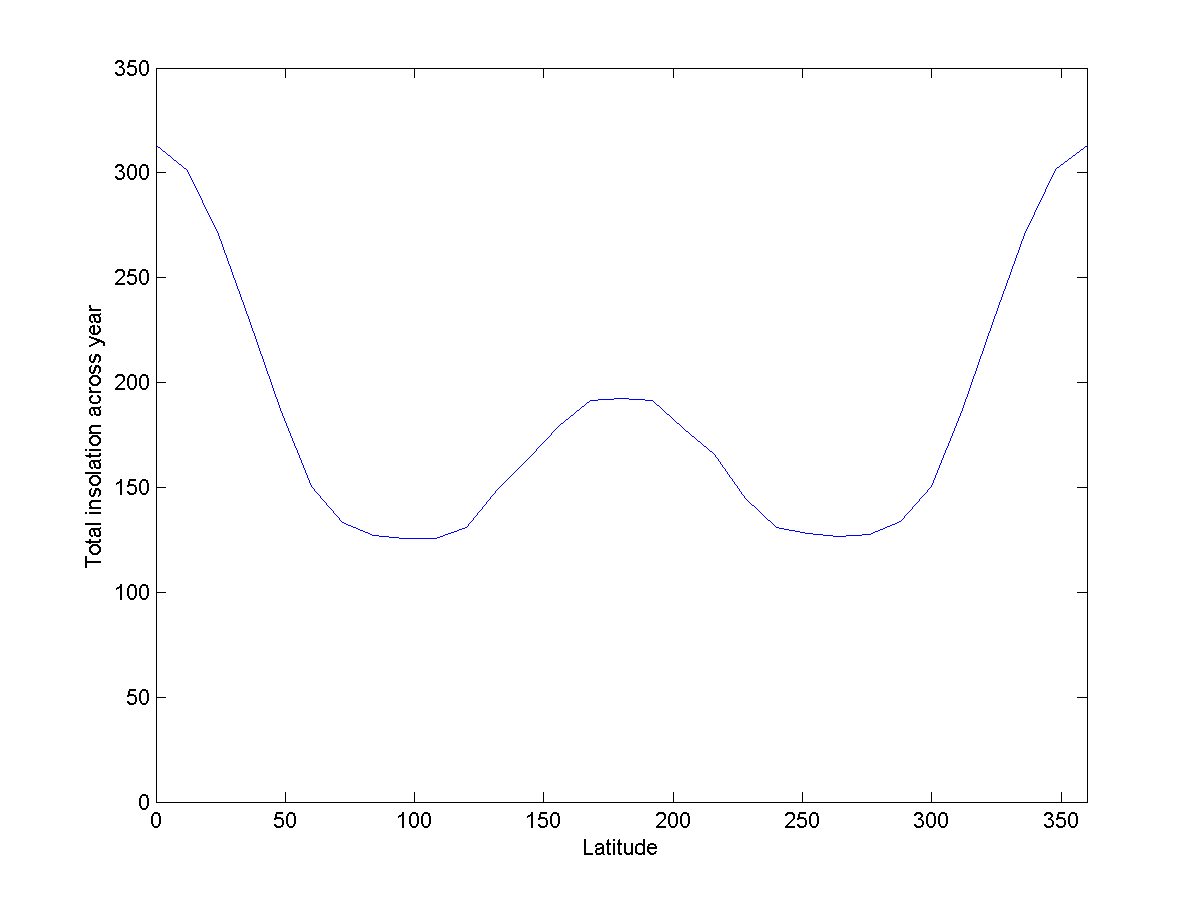 Fig. 11: energy received during the year at different latitudes of the Hoop
Fig. 11: energy received during the year at different latitudes of the HoopCompared to Donut, it will be non-intuitive — the inner equator receives more light during the year than the polar regions. It can be expected that the climate will resemble the Earth - the polar regions are colder, the equatorial ones are warmer. But at the outer equator of the sun there will still be 60% more.
45 degree slope
Perhaps the most surprising discovery awaits us when tilting to a sufficiently large degree - it turns out that in this case there will be four cold and four hot zones on the planet!
The easiest way to imagine this is to think about a spherical planet with an axis tilted at 90 degrees - such as Uranus. Half a year the north pole is turned toward the sun, and most of the hemisphere is constantly lit. As the equinox approaches, the axis begins to look sideways, and the planet is illuminated evenly. The end result - the poles heat up more than the equator. On the toroidal world, the same thing will happen, but the polar regions will be circular there.
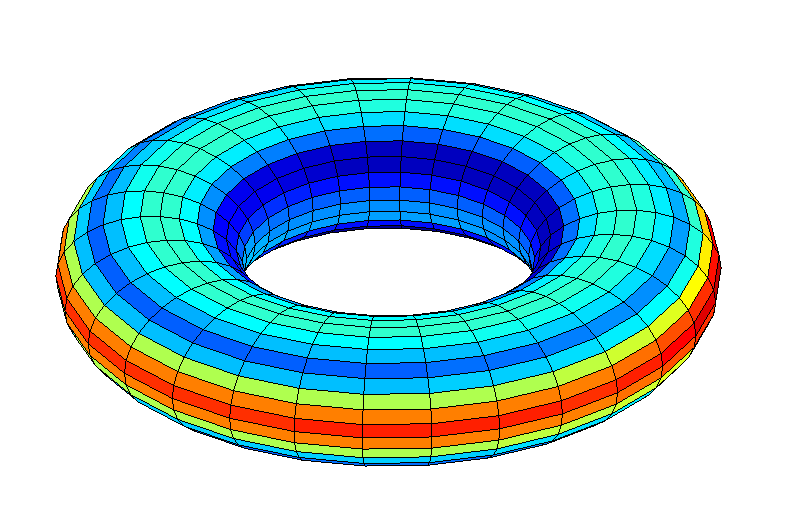 Fig. 12: energy received during the year at different latitudes of the Hoop in the event of a 45 degree tilt
Fig. 12: energy received during the year at different latitudes of the Hoop in the event of a 45 degree tiltAt the Hoop, the difference will not be so big, about 10% of the total coverage. The outer equator is slightly warmer than the polar regions and the inner equator.
A donut has a bigger difference, but in practice medium warm polar regions prevail on most of the surface. The outer equator is only slightly warmer than its neighboring temperature zones.
Geosphere
The surface area is larger than that of the Earth, and the ratio of the volume to the area is less (at the donut it is 1300 km, at the Hoop 1500 km, at the Earth - 2124 km). In this regard, it can be expected that more thermal energy will leak out, with the result that volcanic and tectonic activities will not be as strong. However, even a small amount of tidal heating due to the influence of the sun can release quite a lot of angular momentum energy. In the case of a Hoop inside the planet, there will be 6 times more radioisotopes than on Earth, but only 5 times the surface.
The continental drift will be affected by the difference between the external and internal radii. A circle located on r closer to the center from a circle of radius R will be shorter by 2 π r km, and the relative change will be expressed in terms of r / R. Therefore, on the hoop of the continental plate, moving from the outer equator through the pole to the inner one, it will be necessary to shrink to 43% of the original size. The effect on the Donut is even bigger - it will shrink to 12% of the size! Therefore, continental plates moving to the center will fold, and plates moving to the outskirts will split. So closer to the inner equator the landscape will be very crossed.
Gravity affects the height of the mountains. The difference between the Hoop and the Earth will be small, but at the Ponchik the mountains at the poles can be 1.5 times larger (up to 12 km), and near the equators 3 times more (24 km). Given the overall wrinkled surface next to the hole, the landscape can be quite impressive.
Fast rotation will result in a strong magnetic field. But unlike the Earth, there will be no polar lights in the polar regions, since the lines of the fields will not cross the surface. Counting toro dynamo currents may be interesting, but this is not my level.
Atmosphere
We found that the illumination will change much faster, so the planet must have quite strong winds, transmitting heat from the hot illuminated areas to the cold and dark. But rapid rotation means that the Coriolis force will have a significant effect on wind and current.
The Coriolis force causes the air moving to or away from the axis of rotation to bend, because its speed is different from the speed of the surface. The air section “resting” near the equator actually has a large impulse, because the equator moves rapidly around the axis of rotation: if this air flows to the pole, it will have a noticeable speed directed to the west or east. Therefore, the total air flow is not limited to simple convection from the equator to the poles: when heat is transferred by air, it moves to the pole, twists and creates trade winds.
On toroidal worlds, the rotation speed is 8 times faster than the Earth's, and the difference in speeds is greater. The air turns much stronger, creating narrower climatic zones than on Earth. It is difficult to say how narrow they will be without conducting detailed atmospheric calculations, but this will be more like Jupiter than Earth. This means that heat transfer will be less efficient - there will be more temperature differences between hot and cold areas.Most likely, there will be an intratropical convergence zone.(Intertropical Convergence Zone, ITCZ) around the external equator, where winds converging from the north and south will blow to the west (trade winds), and warm air will rise, move away from the equator, cool and descend at high or low latitudes (where there must be big deserts). Perceptible seasonality, especially on Ponchik, will shift ITCZ north and south, which in some regions will lead to the appearance of monsoons. However, the fast rotation will make the Hadley cell thinner than 30 degrees on Earth (how thinner it is quite difficult to estimate, since it still depends on the gravity changing on the breadth).A large change in temperature at short distances indicates the presence of severe weather conditions, although it is rather difficult to understand exactly what they will be. Especially closer to the hole on the Donut, the seasonal weather will be very wild: warm air from the lighted side will flow through it, twisting into a large funnel, and it will be balanced by a cold wind from the dark side circulating in the opposite direction.Height scales, pressure drop with height, proportional to gravity. Therefore, on Ponchik, the clouds will be 1.5–3 times higher than the terrestrial ones, and on the Hoop they will not differ much from the terrestrial ones.Like on Earth, cyclones can form at middle latitudes. The greater influence of the Coriolis force will lead to the appearance of denser hurricanes - about four times less. However, on Ponchik they will last longer (since a large scale of height gives them more air for development). Wind speeds depend on temperature differences between the surface of the ocean and the upper part of the atmosphere, which can vary greatly throughout the year.Hydrosphere
The amount of water on both worlds is not much different from the earth, although on the Hoop, with a mass of 6 times more, the area will be only 5 times larger, so the volume of water on it will be 20% more due to the initial accretion (therefore, with the same areas of the oceans will be deeper by 20%). Increased mass may attract more comets, but it is difficult to assess how much.Greater seasonal fluctuations in temperature will be more pronounced further from the oceans: the continents at the poles will have more extreme weather than at the equator. Their ability to maintain polar caps during polar summer depends on their configuration and background temperature; since the ice effectively reflects the sun's rays, and the Coriolis force can keep these areas from warming up, the presence of such caps is quite likely. The same can be said about sea ice, although warm sea currents may appear here. Since the flow of water in the ocean is limited to the shape of the basin, the Coriolis force will simply provide circular rotation and will not prevent flows from north to south. Large oceans, such as the Pacific, will be more stretched from west to east.Low gravity near the equator will lead to the appearance of high waves on the Ponchik: you can expect them to be three times the size of the earth. At the poles of the Donut the waves will reach 150% of the earth. The hoop will be closer to the usual waves (133% at the equator, 90% at the poles). Bad weather in the period of summer and winter closer to the center of the Donut will lead to the appearance of giant storm waves.Biosphere
Based on these considerations, it is possible to imagine the presence on the Ponchik and the Hoop of a biosphere that is quite similar to the earth one. On Earth, creatures have adapted well to storms, bad weather, and long winters. Ecosystems can vary in an interesting way depending on the latitude, since there are more differences between the belts than on Earth (gravity, seasonality, temperature). Also, at least on the Hoop, each belt will have much more area - more space for a variety of species in each ecological niche.The moon
Can these worlds hold the moons?A moon orbiting in the equatorial plane in a circular orbit near the toroid will not feel different from a round planet. However, when acquiring eccentricity, everything will become more complicated. When approaching the planet, the potential field falls more slowly than 1 / r, as in normal planets: the Kepler ellipse is no longer suitable as a solution. With the inclination of the orbit, the system becomes even more complex - now the moon will feel the flatness of the planet.In a sense, satellite developers are already facing a similar problem: the Earth is sufficiently flattened at the poles to make it noticeable. This problem was solved in the early stages of space flight (Wikipedia, (Tremaine & Yavetz 2013) or (Nielsen, Goodwin, & Mersman 1958)).In fact, the elliptical orbit is subject to precession - it gradually changes direction, and in the case of the Earth it depends on the inclination of the orbit. Eccentricity can also swim. In any case, for a toroid, these effects will be more pronounced. They will be so strong that the standard calculation methods no longer work, and we will have to carry out computer simulations.I am sure that the moons in fairly distant circular orbits will behave quite stably. Most likely, they will be subject to precession, so their orbit will be more like an outlet than an ellipse, but they will not fly off the coils. Of course, if the moon's orbit is closer, everything will be different.In the simulation (I did not use the full torus, but a ring of 30 masses) I had several possibilities. Equatorial elliptical orbit looks neat and stable, but the precession turns it into a socket.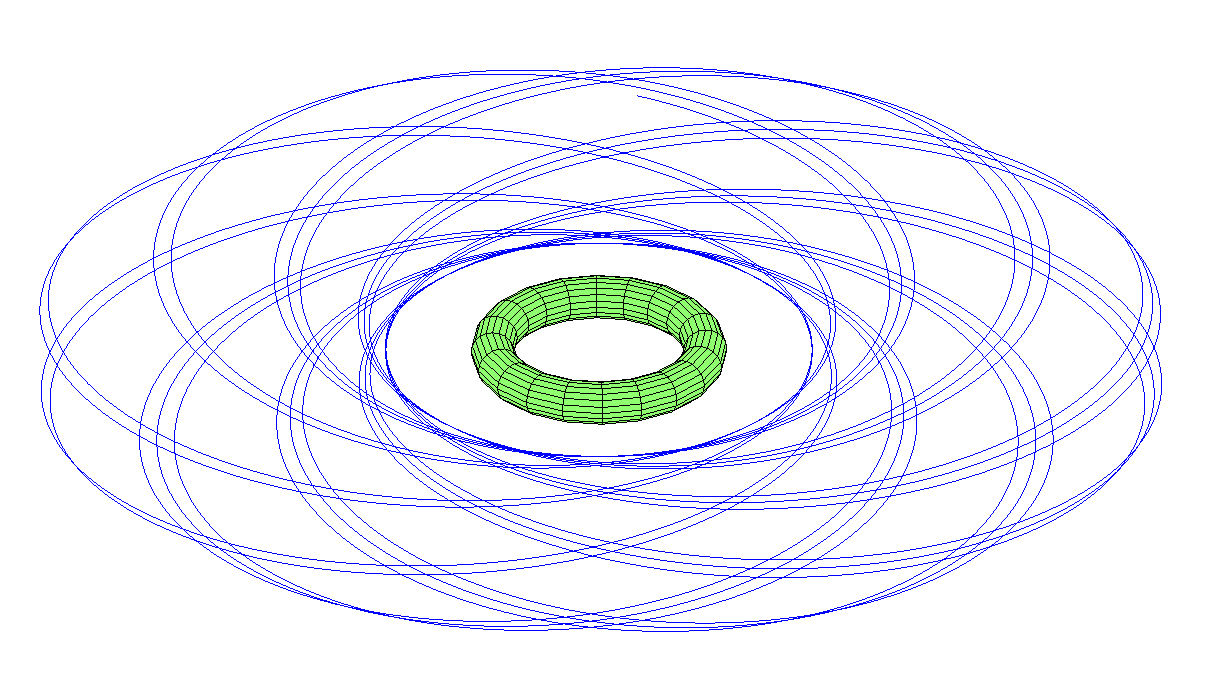 The circumpolar orbit precesses even more; not only the socket appears, but also the precession of the plane. The moon in the sky can appear in any constellation.
The circumpolar orbit precesses even more; not only the socket appears, but also the precession of the plane. The moon in the sky can appear in any constellation.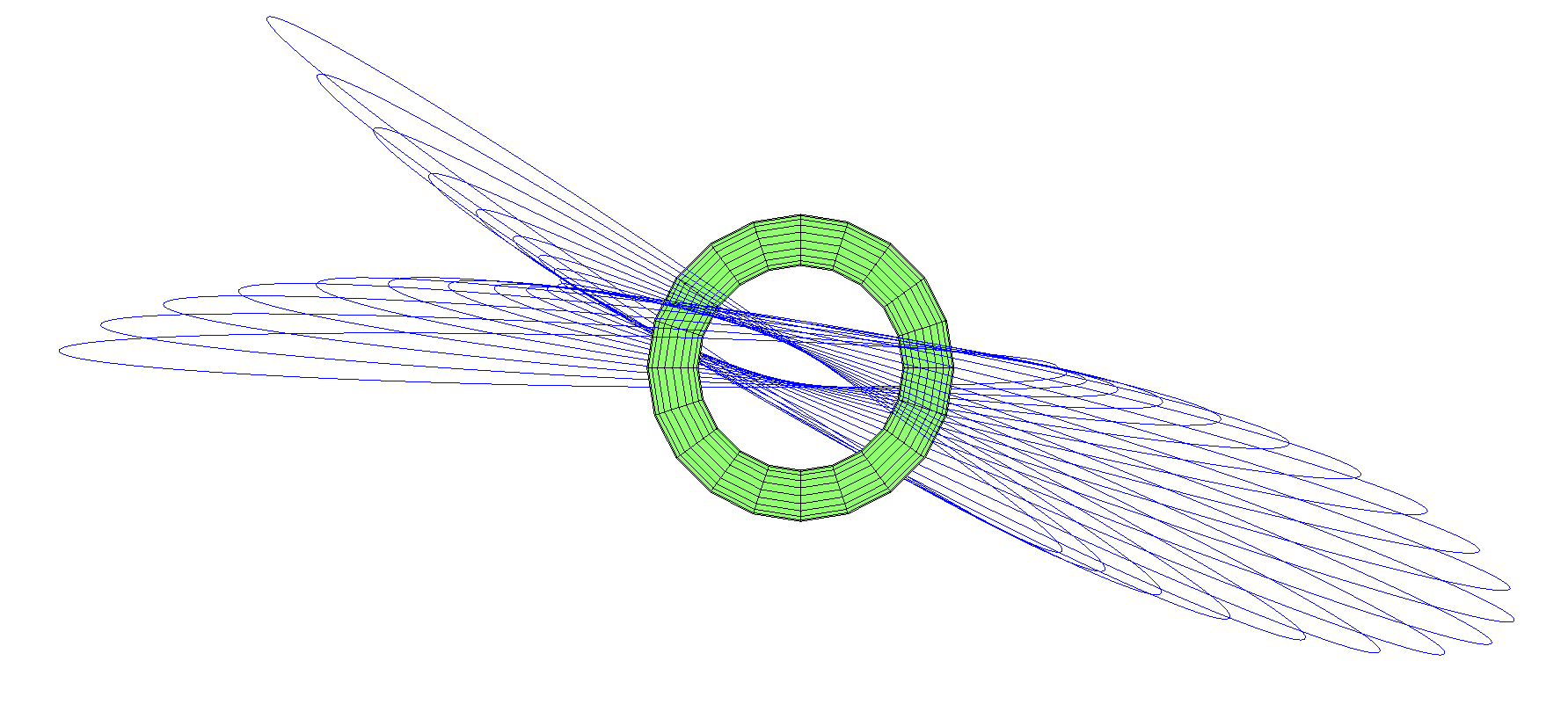 What about orbits passing through a hole? As I noted earlier, the geometric center is an unstable Lagrange point. If you place the moon there, then any blow will knock it out. But there are stably looking orbits through the center (more precisely, with any impact they will turn into another orbit of a similar shape). The simplest option is the moon, dangling to and fro through a hole, like a pendulum:
What about orbits passing through a hole? As I noted earlier, the geometric center is an unstable Lagrange point. If you place the moon there, then any blow will knock it out. But there are stably looking orbits through the center (more precisely, with any impact they will turn into another orbit of a similar shape). The simplest option is the moon, dangling to and fro through a hole, like a pendulum: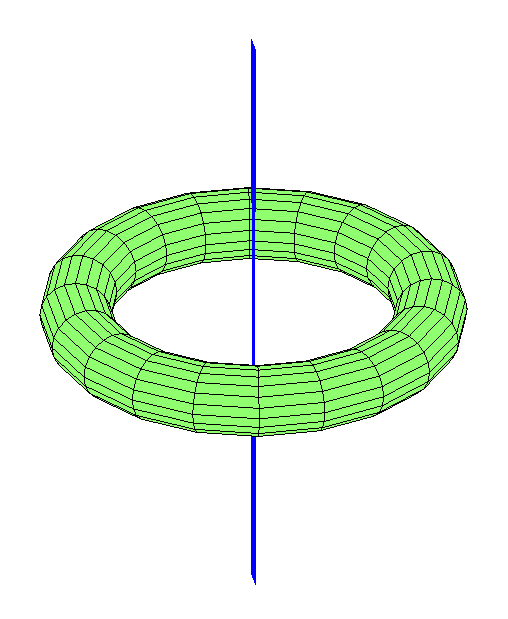 You can imagine the moon flying at a certain longitude:
You can imagine the moon flying at a certain longitude: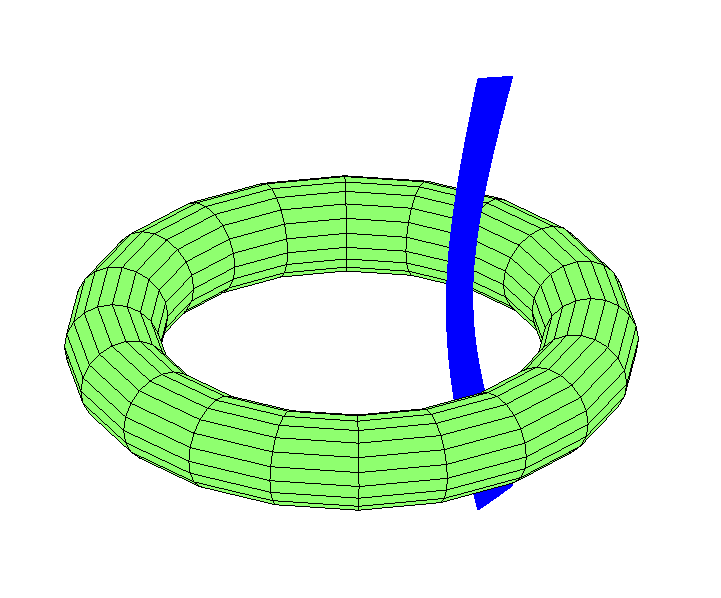 With the acquisition of speed in longitude, it will move in the hole:
With the acquisition of speed in longitude, it will move in the hole: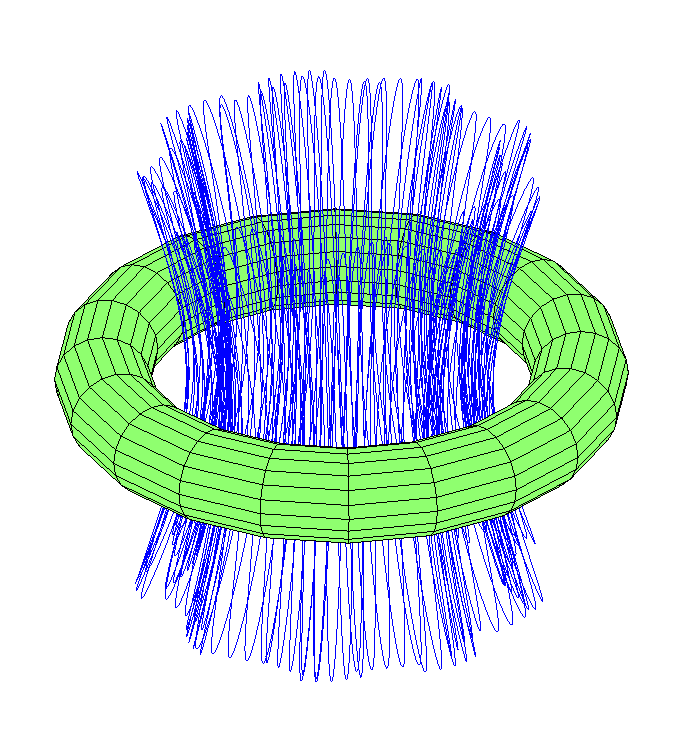 What about the trajectories passing through a hole in one direction? It turned out that there are quite a few eight-orbits that draw a large toroidal tangle.
What about the trajectories passing through a hole in one direction? It turned out that there are quite a few eight-orbits that draw a large toroidal tangle.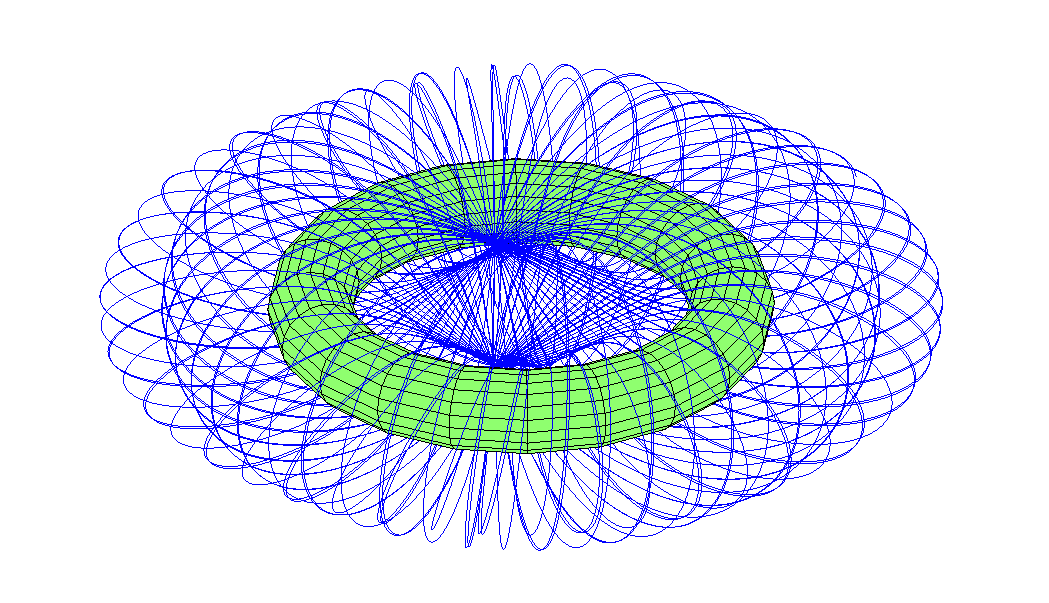
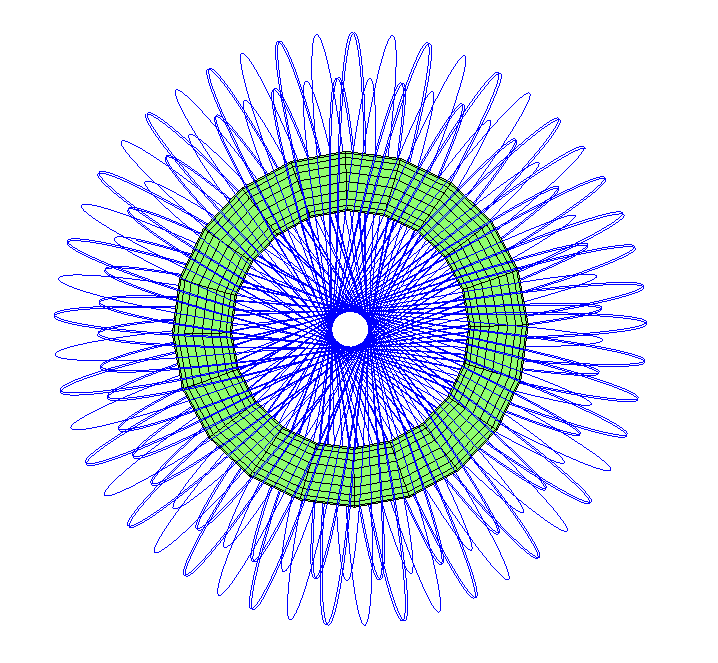 Note that the orbit is slightly elongated. From the "apogee", above the external equator, it passes through a hole, appears on the back side, where it experiences perigee at the point opposite to the initial one. Then it again passes through the hole, and comes out near the place where the movement began - but the precession twists it along the torus.These simulations should be perceived as primary drafts — real calculations require more precision. My numerical accuracy is not enough to assess long-term stability. The gravitational fields of the Donut and Hoop look even more complicated due to their flattening, and the sun and other planets will also contribute.
Note that the orbit is slightly elongated. From the "apogee", above the external equator, it passes through a hole, appears on the back side, where it experiences perigee at the point opposite to the initial one. Then it again passes through the hole, and comes out near the place where the movement began - but the precession twists it along the torus.These simulations should be perceived as primary drafts — real calculations require more precision. My numerical accuracy is not enough to assess long-term stability. The gravitational fields of the Donut and Hoop look even more complicated due to their flattening, and the sun and other planets will also contribute.Tidal forces
Tidal forces are a problem. Imagine the moon moving around a toroid. Behind it are bloated water and stone. Rapid rotation will push the swelling forward of the moon (if the moon moves in the direction of rotation of the planet and is above the geostationary orbit). The attraction of the bulge will itself drag the moon forward, giving it an acceleration - and in space it forces the moon to move in a higher orbit. That is how the Moon took a lot of the angular momentum of the Earth, slowed its rotation and moved away from it. In the case of rapid rotation, like our toroids, the effect will be more noticeable: the moons will fly away from the planet and probably get lost.What will happen to the moons that are close, below the geostationary orbit? They will move faster than a bulge that will slow them down. Orbit will decrease. Soon they spiral down and turn into giant meteors. The same thing happens with moons moving in the opposite direction. Of course, if the moon is big enough, tidal forces can break it and turn it into a ring.Wider orbits passing through a hole are likely to lose stability. Pendulum orbits will acquire an angular momentum due to swelling, and the moon will move faster and faster until it flies away from the planet, or falls. Some G8 orbits can come into resonance and acquire and lose energy in equal shares, but they will be lurked by a similar problem. So, most likely, toroids will not have truly exotic moons. However, no one forbids launching artificial satellites with orbit support. Pendulum orbits can be useful for communication satellites on the inner surface of a torus.Total
Toroidal worlds are unlikely to appear naturally. But if they do, these will be amazing places to look for adventures. Large surface area. Regions with a very different climate, seasons, gravity and ecosystems. Amazing sky on the inside. Unchecked weather. The moons in strange orbits.It would be nice to learn how to create them not only in simulations.Anders Sandberg is a researcher, scientific debater, futurologist, transhumanist, and writer. He received his Ph.D. in computational neuroscience at the University of Stockholm, and is currently a research fellow at the James Martin Research Society at the Institute for the Future of Humanity at Oxford University.