 This is hohlraum
This is hohlraumThe National Ignition Equipment, a unique complex of the National Ignition Facility in the Livermore Laboratory named after Lawrence (USA), provides experiments with inertial thermonuclear fusion. It is the most powerful laser system in the world and a unique laboratory complex. Everything related to equipment and technical solutions deserves top marks and is very expensive.
The place where the thermonuclear microexplosion should occur is called the German word hohlraum. A gold chamber, which should provide uniform heating of a thermonuclear tablet by electromagnetic energy emitted by the walls. Something similar with the same name and for the same has a "hydrogen" bomb. Only larger, and the source of photons is X-rays from the primary nuclear explosion, penetrating the hohlraum through the radiation channel (interstage).
Through the two inlets, the interior of the gold chamber is illuminated by 192 ultraviolet laser beams with a total power of up to 500 Terawatts. In 3–5 nanoseconds, 2–4 MJ of energy comes in, which must be re-emitted by the walls in the X-ray range. A thermonuclear tablet contains 15 micrograms of deuterium and tritium at a temperature of 18 K, as well as gas injected into the internal cavity. The capsule has a spherical shell with a diameter of 2 mm. Its ablating coating can be made of beryllium or has a composite structure based on polyethylene. It absorbs up to 100 KJ of energy, resulting in a radiation implosion of the capsule. The density of the substance reaches 1000 g / cc, and the temperature of the deuterium-tritium filling rises to hundreds of millions of degrees. After that, she is left with only one thing. Explode like a thermonuclear bomb or light up like a star - someone you like more.
The estimated yield of a microexplosion can reach 20 MJ, which is equivalent to 5 kg of TNT. Formally, efficient, controlled, inertial, thermonuclear fusion will take place. In fact, taking into account the efficiency of the laser system no more than 1%, this technology will not lead to a practical source of energy. Only for charging the capacitors that feed the laser amplifiers, 420 MJ is required. But the goal of NIF is not power generation, but fundamental science.
However, the energy efficient reaction, i.e., “thermonuclear burning” stubbornly fails. Although the reaction takes place to be. The New York Times published on October 6, 2012 a critical note that the
NIF program
did not achieve the stated goals and is not a fact that it will ever reach . Today we can conclude that the goals of the NIF are not achieved. Thermonuclear fusion stubbornly does not burn, on what tricks did not go Livermore!
It can be assumed why this
should have happened. Spherically symmetric compression of the capsule is possible only in the state of thermodynamic equilibrium. In this case, the surface temperature of the capsule at each point is the same, which provides a symmetrical ablation. Suppose that events in hohlraume-e occur as theorists of the NIF project imagined.
Then, soon after the start of X-ray irradiation (we are talking about fractions of a nanosecond), the surface of a spherical capsule is heated to tens of millions of K and an ultrathin plasma layer is formed, which is in (quasi) equilibrium with radiation. This means that the near-surface plasma layer emits about as much electromagnetic energy as it receives, but also radiates it inwards. The latter leads to the heating of the capsule in depth and, accordingly, to the thickening of the plasma layer. As the distance from the outer surface increases, its temperature decreases until the radiation inwards becomes negligible. In this case, the radiation to the outside becomes equal in intensity with the radiation falling on the capsule, i.e. balance will come. At the same time, the plasma layer expands due to pressure, which is the most essential part of the ablation process for implosion.
Fundamentally important is the fact that in the process of ablation, the surface of the capsule is in thermodynamic (quasi) equilibrium with radiation. This allows you to estimate the amount of energy entering the capsule using the Stefan-Boltzmann law to emit a black body:
Where
- radiation intensity (W / m2) from the surface or falling on the surface heated to the temperature
Kelvin
- Stefan-Boltzmann constant (in SI).
It follows that the radiation incident on the capsule has a Planck spectrum corresponding to the temperature
capsule surface. This is what this spectrum looks like at
K where
- the proportion of photons with energy
in the total number of photons emitted per second (we are talking about the energy distribution density of the number of photons).
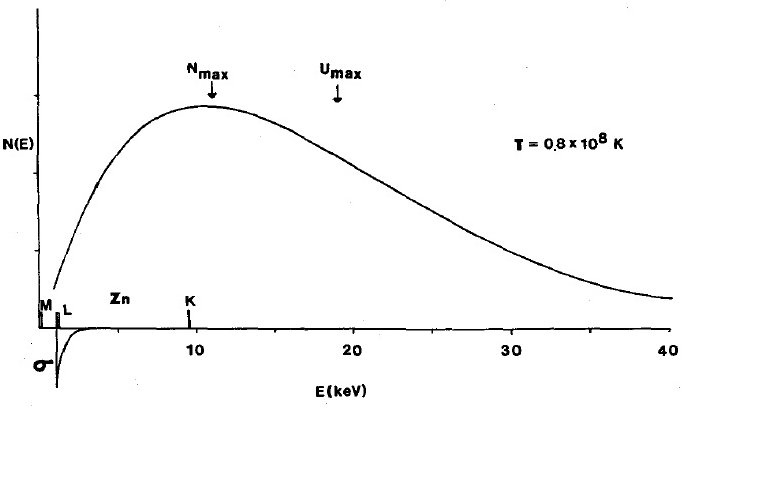
In this spectrum, the highest photon flux density falls on energy slightly above 10 KeV, which corresponds to X-rays with a wavelength of about 1 Angstrom. This is a typical radiation spectrum in the zone of radiation diffusion in a nuclear bomb explosion (approximately 0.5 microseconds after the start of a chain reaction, about a meter from the zero point, there is still no dazzling flash).
But where do the photons of such a hot Planck spectrum come from, watering the capsule outside? There are almost no such photons in laser beams. They emit the walls of the hohlraum, heated by the rays of a mega-laser. At least that's what the NIF theorists thought.
However, here they came into conflict with the very concept of hohlraum, since this term means a chamber whose inner walls are in equilibrium with radiation. But the lower ultraviolet (essentially optical) laser radiation falling on the chamber walls cannot be in thermodynamic equilibrium with thermal radiation obeying the Stefan-Boltzmann law.
At the same time, a plasma layer with a temperature is also formed at the wall surface.
close to 100 million K. The plasma emits and absorbs radiation, like a completely black body. Consequently, the radiation absorbed by the plasma layer at the chamber walls has a Planck spectrum at
. But this is not so if only because the incident radiation is laser. In addition (and this is more important!) - among the photons in the laser beams there are no energies of ~ 10 KeV. The energy of photons arriving at the hohlraum outside is 3–4,000 times smaller. Therefore, the walls of the hohlraum cannot be in equilibrium with the radiation. But thermodynamic (quasi) equilibrium will inevitably occur as the plasma layer forms and heats up, just as described above for a capsule. There is a contradiction!
Here a reasonable question may arise: but do I not contradict myself when, on the one hand, I consider the near-surface plasma layer to be thermodynamically balanced, and on the other hand I assert that its temperature falls in depth. No, I do not contradict, because it is quasi-equilibrium. In other words, a sufficiently thin outer plasma layer can be considered equilibrium with radiation and therefore radiating as well as absorbing energy in the Planck spectrum. That is why I often write about the thermodynamic (quasi) equilibrium of a
surface with radiation. Someone may ask: why does this thin layer radiate in both directions for as much energy as it receives from one c to one? Is there a contradiction with the law of conservation of energy? There is no contradiction, because This thin layer also receives energy from the adjacent layer of plasma lying deeper.
 This is what the NIF building looks like. Almost everything is filled with a laser machine.
This is what the NIF building looks like. Almost everything is filled with a laser machine.Thus, the picture of the events in the gold chamber, drawn by the imagination of the theorists from Livermore, does not correspond to reality. Where did they get the idea that in this way you can arrange in hohlraum something similar to what happens in a thermonuclear bomb, where it is by no means optical, but x-ray photons from the first-
stage explosion
water the second ?
They took it from successful experiments on laser X-ray generation in thin foil, illuminated by a super-powerful optical laser, and others like that, which were many carried out in the 90s. But, apparently, there was no blackbody radiation, corresponding to a temperature of about 100 million K, and the plasma as a whole was not heated to such a temperature. In other words, these processes were thermodynamically nonequilibrium. It is worth noting that the energy of laser radiation, which was observed in this case, was negligible compared to the heating energy.
That is why, despite the concentration of colossal and seemingly sufficient energy, thermonuclear fusion “does not burn”, although the reaction takes place (synthesis is possible in principle even at room temperature, since the tail of the Maxwell distribution approaches zero, that's all detect such a reaction is unlikely to work) Apparently, with the help of NIF, in principle, it is impossible to achieve uniform heating of the capsule to a sufficiently high temperature, as it does in a thermonuclear bomb.
But what happens in this case? Where does the energy of the laser beams, which theoretically should have heated the substance of the capsule to 100 million K? It can be assumed that there is a premature expansion of the capsule and mixing it with the golden plasma. Or mixing deuterium and tritium with a capsule substance. As a result, even if the temperature in hohlraum-e reaches the desired values, the pressure required for the synthesis in the reaction zone is absent. But perhaps more importantly: the thermodynamic equilibrium of the chamber walls and the surface of the capsule with radiation is not achieved, which leads to uneven heating. Spherical implosion does not work!
As can be seen from the previous arguments, in order for inertial thermonuclear fusion to work, it is necessary to irradiate the capsule with X-ray photons. That is, you need to reproduce in thumbnail. radiation implosion mechanism used in a thermonuclear bomb. An X-ray source with sufficient intensity is a
hypothetical X-ray laser pumped by a nuclear explosion. Since photons with an energy of ~ 10 KeV are needed, the pumping power should be hundreds of kilotons or, possibly, megatons. Of course, the idea to set fire to synthesis in a volume of ~ 1 cube. mm by the explosion of a megaton is absurd.
Today, experiments with free-electron X-ray lasers are actively conducted. For generation at a wavelength of 1 Angstrom, they must be coupled with large electron accelerators. This is no less a cyclopean structure than an NIF. But maybe in this way it will turn out to light a thermonuclear bomb or a star in miniature - as you like. Although X-rays reflect very poorly, it will be very difficult to focus them.
Final remarks.
- Quasi-equilibrium is called the instantaneous state of a nonequilibrium process, which can be considered an equilibrium state with a negligible error.
- The proposal to use an X-ray laser to heat up a thermonuclear tablet does not contradict the statement that radiation should fall on the capsule wall should have a Planck spectrum. It will have approximately the same spectrum due to the inelastic scattering of x-ray photons on the walls of the hohlraum.
- Surely in my reasoning you can find a lot of formal inaccuracies. This is still not a scientific, but a popular science article. But still, it seems to me, the essence of the main problem of NIF in this article is reflected correctly.
- In particular, if in NIF it is intended to irradiate the capsule not with X-ray, but soft X-ray (or hard ultraviolet) photons at a temperature of several million K (that is, far from 100), then in this case the above arguments against NIF remain valid. Namely: Planck's emission spectrum of the hohlraum walls with a peak of ~ 1 KeV or even ~ 0.1 KeV cannot occur with a laser absorption spectrum with photons of ~ 1 eV if there is thermodynamic (quasi) equilibrium. If it does not take place, then a spherically symmetric implosion is impossible.