 Particles of the standard model, with masses indicated in the upper left corner. Three left columns occupy fermions, two right - bosons
Particles of the standard model, with masses indicated in the upper left corner. Three left columns occupy fermions, two right - bosonsThere are only two types of fundamental particles in the entire Universe: fermions and bosons. Each particle, in addition to the usual properties known to you, such as mass and electric charge, has its inherent amount of angular momentum, known as spin. Particles with half-integer spins (± 1/2, ± 3/2, ± 5/2, ..) are known as fermions. Particles with whole spins (0, ± 1, ± 2, ..) are bosons. There are no other particles, fundamental or composite, in the Universe. But why does it matter? Our reader asks:
Could you explain the difference between fermions and bosons? What changes when moving from a whole spin to a half-integer?
At first glance, the breakdown of particles into categories according to such properties seems random.
 Known particles in the Standard Model. These are all fundamental particles, directly discovered. A graviton, while unopened, has a spin of 2.
Known particles in the Standard Model. These are all fundamental particles, directly discovered. A graviton, while unopened, has a spin of 2.After all, a particle is a particle, isn't it? Of course, there is more difference between quarks (exposed to strong interaction) and leptons (not exposed to it) than between fermions and bosons? Of course, the difference between matter and antimatter means more than spin? Is the presence or absence of mass much more than something as trivial as the angular momentum?
It turns out that several small, significant, differences are associated with spin, but there are two serious differences that have much more significance than most people think, and even most physicists.
 Photons, particles and antiparticles in the early universe. It was filled with bosons and fermions, as well as with all representable antifermions.
Photons, particles and antiparticles in the early universe. It was filled with bosons and fermions, as well as with all representable antifermions.The first is that only fermions have copies among antiparticles. Antiparticle for quark - antiquark. The antiparticle of an electron is a positron, while a neutrino has an antineutrino. Bosons, on the other hand, are antiparticles of other bosons, and many bosons are antiparticles themselves. There is no such thing as antiboson. Face photon with another photon? Z
0 with another Z
0 ? This is the same from the point of view of the interaction of matter and antimatter, as the annihilation of the electron and positron.
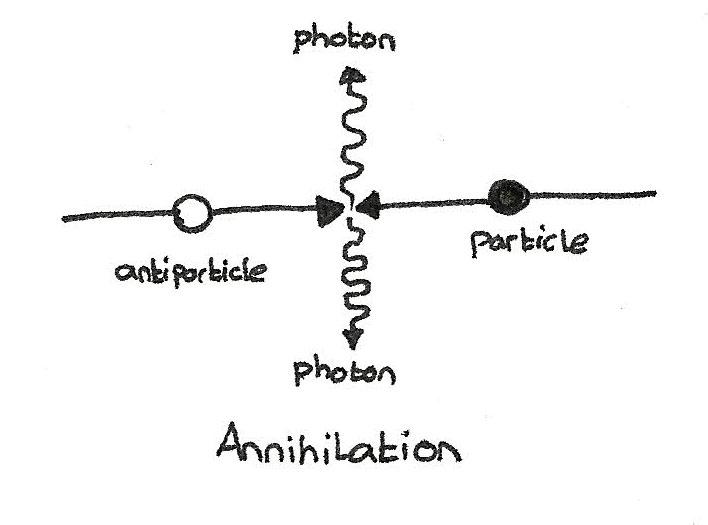 A boson - such as, for example, a photon - may be an antiparticle itself, but fermions and antifermions are different (like an electron and a positron)
A boson - such as, for example, a photon - may be an antiparticle itself, but fermions and antifermions are different (like an electron and a positron)Fermions can create composite particles: the two upper quarks and one lower give a proton (fermion), one upper and two lower quarters give a neutron (ferimon). Because of the peculiarities of the spin work, if we take an odd number of fermions and link them together, then a new, composite particle will behave like a fermion. That is why there are protons and antiprotons, and therefore the neutron differs from the antineutron. And particles consisting of an even number of fermions, for example, the quark-antiquark combination (known as the meson), behaves like a boson. The neutral peony π
0 is itself an antiparticle.
The reason is simple: each of these fermions is a particle with a spin of ± 1/2. If you add two particles together, you get an object with a spin of -1, 0, or +1, that is, a whole (and therefore it is a boson). If you add three, you get a spin of -3/2, -1/2, +1/2, or +3/2, that is, a fermion. So the difference in particles and antiparticles is quite large. But there is a second difference, perhaps even more important.
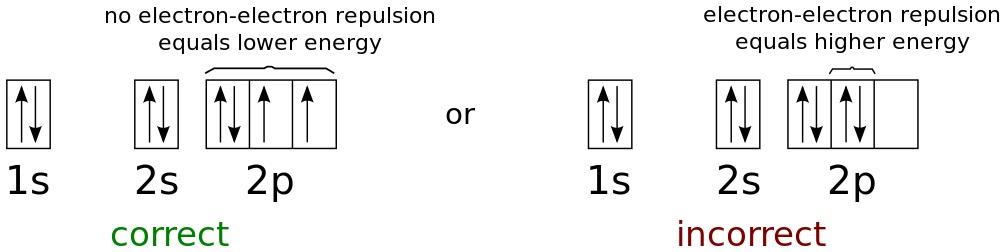 Energy levels for the lowest possible energies in a neutral oxygen atom. Since electrons are fermions, not bosons, they all cannot exist on the first level, even at arbitrarily low temperatures.The Pauli exclusion principle
Energy levels for the lowest possible energies in a neutral oxygen atom. Since electrons are fermions, not bosons, they all cannot exist on the first level, even at arbitrarily low temperatures.The Pauli exclusion principle applies only to fermions, not bosons. He postulates that in any quantum system two fermions cannot occupy the same quantum state. Bosons have no such restrictions. If you take the nucleus of an atom and start adding electrons to it, the first electron will go to the ground state - the state with the lowest energy. Since this is a spin 1/2 particle, its spin state can be either +1/2 or -1/2. If you add a second electron to the atom, its spin will be in the opposite state, and it will also go into the state with the lowest energy. But if you add more electrons, they will not be able to go to the ground state, and they will need to settle at the next energy level.
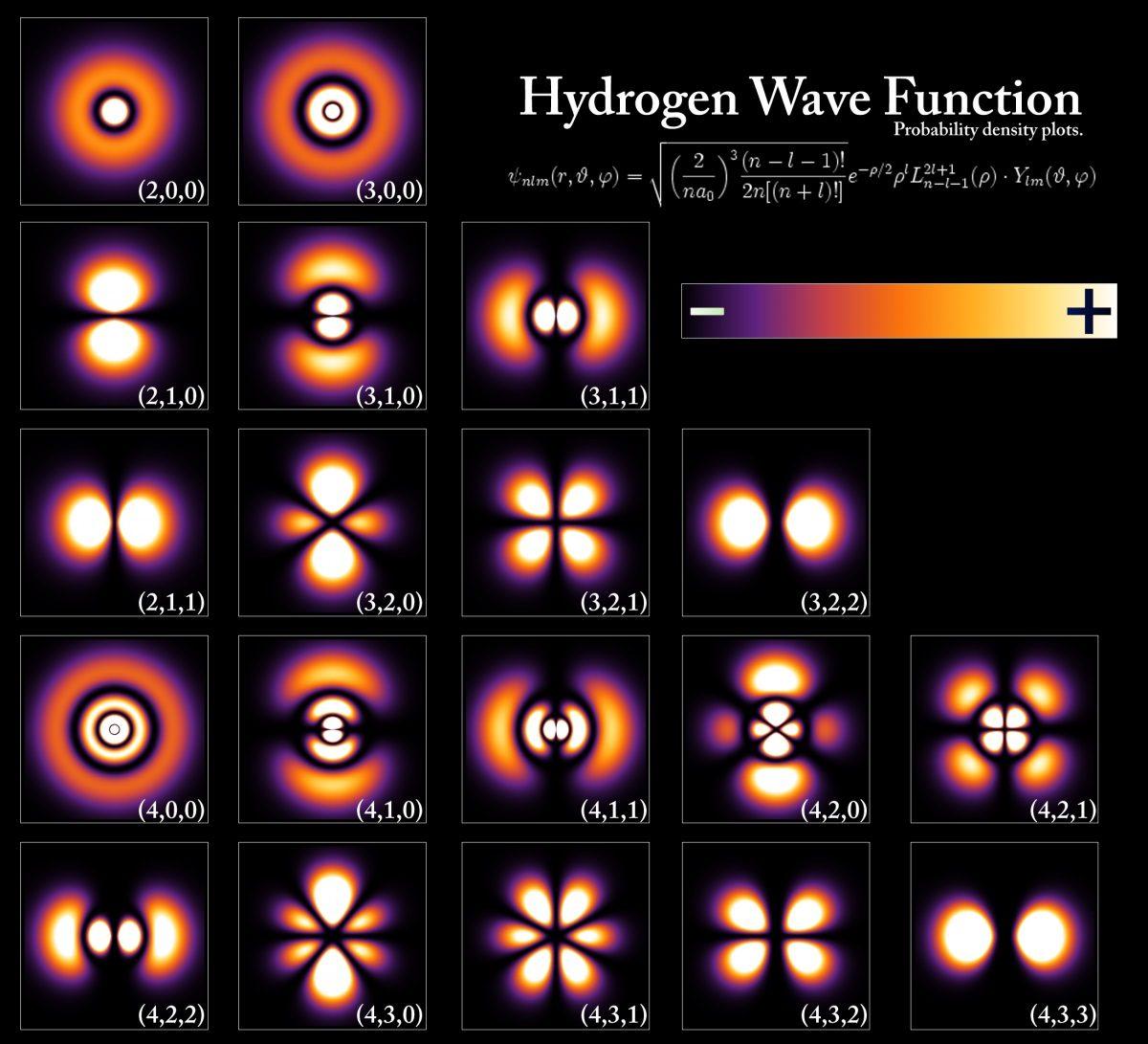 The energy levels and wave functions of electrons corresponding to different states of the hydrogen atom.
The energy levels and wave functions of electrons corresponding to different states of the hydrogen atom.That is why the periodic system of elements of Mendeleev is arranged in this way. Therefore, atoms have different properties, they are connected together in such complex combinations, and therefore each element of the table is unique: the configuration of electrons in each atom is different from all the others. The fact that two fermions cannot be in the same quantum state leads to the appearance of certain physical and chemical properties of elements, to a huge number of molecular combinations and to fundamental connections, due to which complex chemical reactions and life are possible.
 The way atoms bind and form molecules, including organic ones, is possible only due to the Pauli exclusion principle.
The way atoms bind and form molecules, including organic ones, is possible only due to the Pauli exclusion principle.On the other hand, as many bosons can be brought into the same quantum state! This allows you to create special bosonic states, known as Bose-Einstein condensates. By cooling the bosons so much that they go into a state with the least energy, you can place any number of them in one place. Helium (consisting of an even number of fermions, therefore behaving like a boson), at low temperatures turns into superfluid - the result of Bose-Einstein condensation. To date, gases, molecules, quasi-particles, and even photons have been brought into such a state. Active research is still under way in this area.
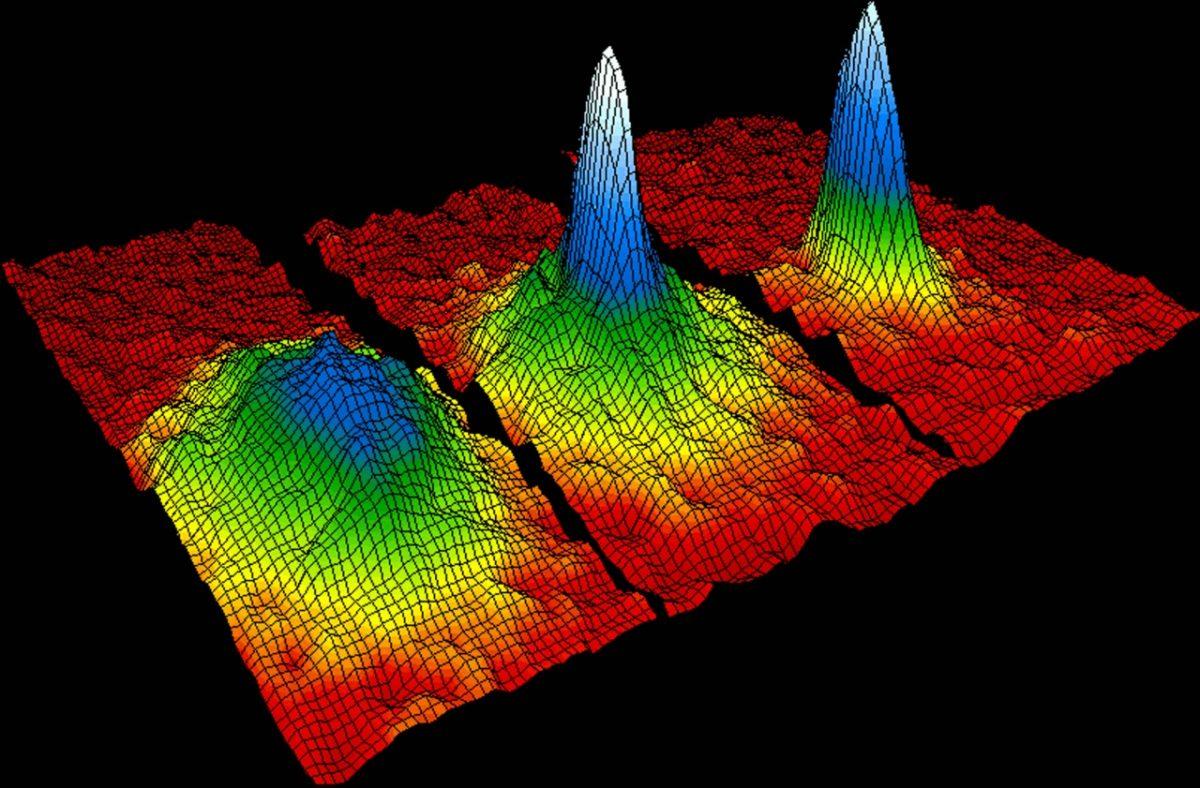 Rubidium atoms before (left), during (in the middle) and after (right) transition to the Bose-Einstein condensate state. The graph shows how atoms condense from less dense red, yellow and green areas into more dense blue and white
Rubidium atoms before (left), during (in the middle) and after (right) transition to the Bose-Einstein condensate state. The graph shows how atoms condense from less dense red, yellow and green areas into more dense blue and whiteThe fact that electrons are fermions leads to the fact that dwarf stars do not collapse under their own weight; the fact that neutrons are fermions, leads to the fact that the collapse of neutron stars stops at some moment. The prohibition principle of Pauli, responsible for the atomic structure, keeps the densest of physical objects from becoming black holes.
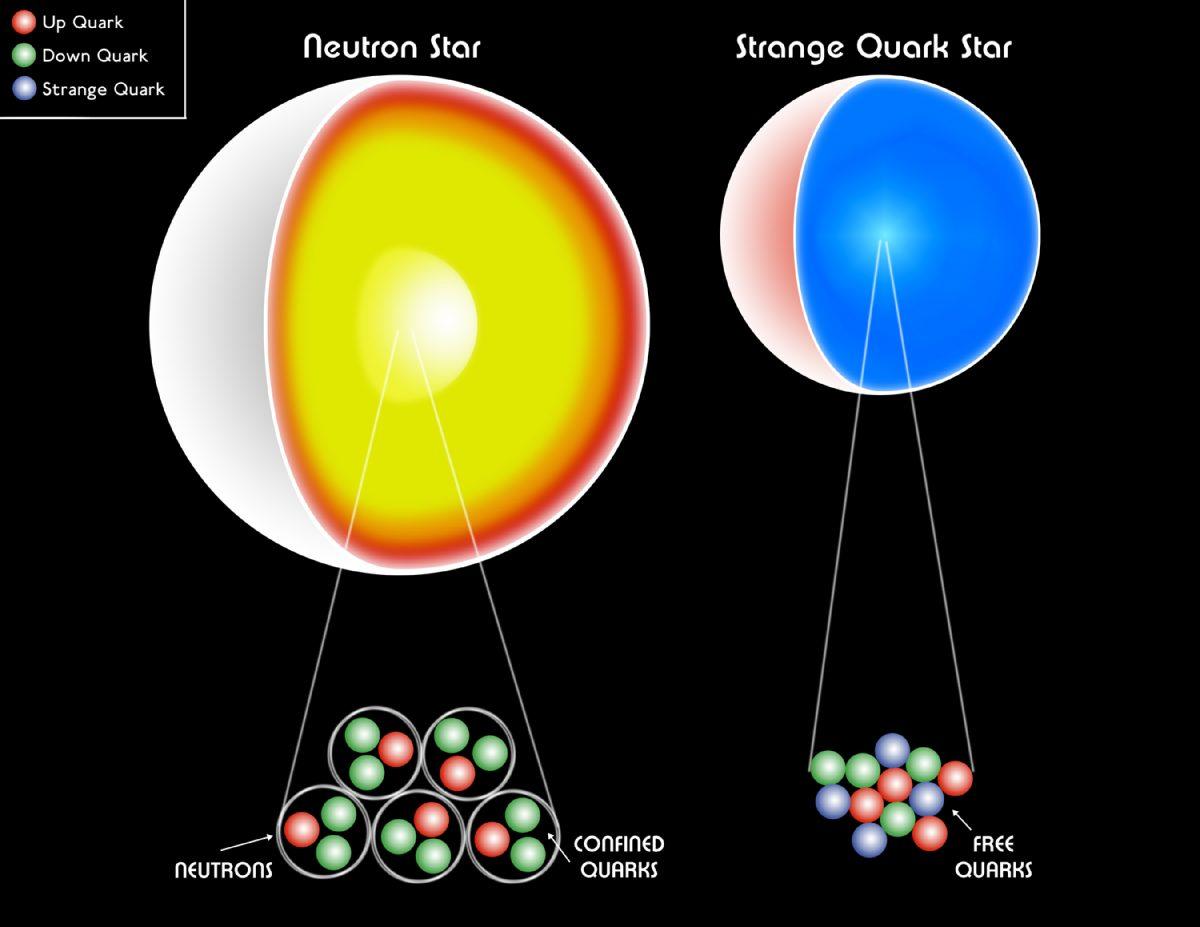 A white dwarf, a neutron star, and even a quark star are still composed of fermions.
A white dwarf, a neutron star, and even a quark star are still composed of fermions.When matter or antimatter annihilates or decays, they heat the system to temperatures depending on whether the particles obey the
Fermi-Dirac statistics (for fermions) or
Bose-Einstein (for bosons). Therefore, today the temperature of the CMB is 2.73 K, and the background neutrino radiation is 0.8 K less: this was due to the annihilation of these statisticians who worked in the early Universe.
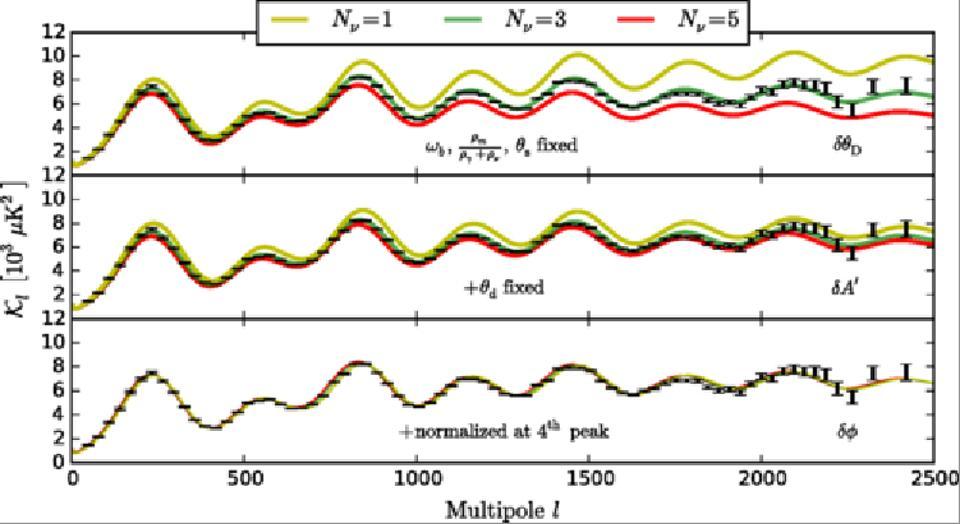 Adjusting the number of neutrinos to coincide with the data on the background radiation fluctuations. The data coincides with neutrino radiation, the energy equivalent temperature of which is 1.95 K - much less than that of the photons of the CMB
Adjusting the number of neutrinos to coincide with the data on the background radiation fluctuations. The data coincides with neutrino radiation, the energy equivalent temperature of which is 1.95 K - much less than that of the photons of the CMBThe fact that fermions spin half-integer, and bosons - whole, is interesting in itself, but it is much more interesting that these two classes of particles obey different quantum rules. At a fundamental level, these differences make our existence possible. This is a good result for such trifles as the difference in ± 1/2 in the internal angular momentum. But the extensive consequences of the seemingly pure quantum rule illustrate how important spin can be, and the difference between bosons and fermions.
Ethan Siegel - astrophysicist, popularizer of science, blog Starts With A Bang! He wrote the books Beyond The Galaxy , and Treknologiya: Star Trek Science [ Treknology ].