When I talk to a person who is far from physics about possible additional dimensions of space, unknown to us, then one of the most frequent questions asked to me is: “How do you imagine additional dimensions? I can only imagine three, and do not understand how to go further; it's meaningless to me. ”
What we, physicists, do not do (at least none of my friends claimed to be doing this), so we don’t imagine additional dimensions. My brain is limited in the same way as yours, and although this brain easily creates a three-dimensional image of the world in which I can move, I cannot make it present an image of a four- or five-dimensional world like you. My survival did not depend on the ability to represent something like that, so it is perhaps not surprising that my brain is not tuned to this.
Instead, (and, judging by our exchange of ideas, most of my colleagues, too) I develop intuition based on a combination of analogies, tricks with visualization and calculations. We omit the calculations here, but many analogies and tricks are not so difficult to explain.
Reflections on additional dimensions can be learned in two stages.
- The simple stage is to learn to represent or describe the world with additional dimensions. You already know several ways to do this, even if you are not aware of it - and you can learn some more.
- The stage is more difficult - to learn how everything in the world with additional dimensions works. How to work with a needle in four dimensions, and not in three; will the planets move in orbits around the sun in six spatial dimensions; will protons and atoms form? Here you will need to learn unfamiliar stunts, presenting the differences between the world with only one or two dimensions and three-dimensional, known to us, the world, and working by analogy.
So let's start by helping you to imagine the world with additional dimensions. To do this, you need to think about how we represent any dimension at all. Start over.
- A world with zero measurements is a point. There is very little to say about him now, but we will return to him.
- One-dimensional world is already quite interesting.
- Much more interesting happens in two-dimensional worlds.
- It is important to avoid confusion between spatial dimensions and the more general meaning of the word “dimension” in ordinary language, as well as in mathematics and statistics.
- And further various examples of additional dimensions will follow, with a focus on what exactly “additional” means, and how it can be that there are dimensions in our world about which we know nothing.
- We will also look at how you can detect these inconspicuous measurements.
One-dimensional worlds
A world with one spatial dimension is much simpler than a world with three, but there is also something in it that can be discussed. For example, there are several types of one-dimensional worlds. They have not only certain common properties, but also interesting differences.
For the first example, let's consider the measurement not as a physical, but as a more general concept. It will help you in many ways, for example, to distract your intuition from natural misconceptions about what measurements are and how they work. Let's talk about annual earnings - how much money a person gets in a certain year. This is the same measurement that is suitable for the study, like all others.
Income measurement
Your last year’s income is a certain number in your local currency. It can be positive or negative, large or small; it can be represented as a point on the line, as in fig. 1, which we will call the "point of income." Each point on the line represents a potential return.
 Fig. 1: income line of infinite length, the left side of which represents losses, the right - income.
Fig. 1: income line of infinite length, the left side of which represents losses, the right - income.What makes an annual income a one-dimensional property is (very roughly) the following:
• Position in space is indicated by one unit of information: in our case, income.
Also note that it is continuous (or almost continuous) - if two people have different incomes A and B, we can find a third one whose income is between A and B.
Two of these facts imply that income can change continuously along the income line, moving to the right or left — either to higher or lower income. There are no other options.
Of course, the income line has nothing to do with the physical space in which we can walk with you, but it is still a measurement. And (at least in principle) he has no end in either of the parties: there is (in principle) no limit on how much money a person can earn or lose in a year. This one-dimensional world is not so diverse, but still we can ask a few sensible questions about it:
- How are annual revenues distributed in the USA?
- What is the average annual income in Japan?
- How do the answers to these questions change over time?
These questions acquire meaning in the one-dimensional world of the income line.
Rainbow measurement
And here is another, a completely different world. The colors of the rainbow form a single dimension, from red, through orange, to yellow, from there to green, [blue], blue and to purple [English-speaking people have six colors in the rainbow, they do not emit blue / approx. trans.]. From this point of view, colors form a one-dimensional world of finite size. Outside of red or purple there are invisible forms of flowers, but from the point of view of your eyes, the measurement ends with them. Now it is presented not in the form of an infinite line, but in the form of a segment - the “rainbow line” in fig. 2. Please do not confuse it with the color wheel - if it is closed, then our measurement starts from red and ends in purple. Again, the position on the rainbow line is determined by one unit of information (color), and it is continuous.
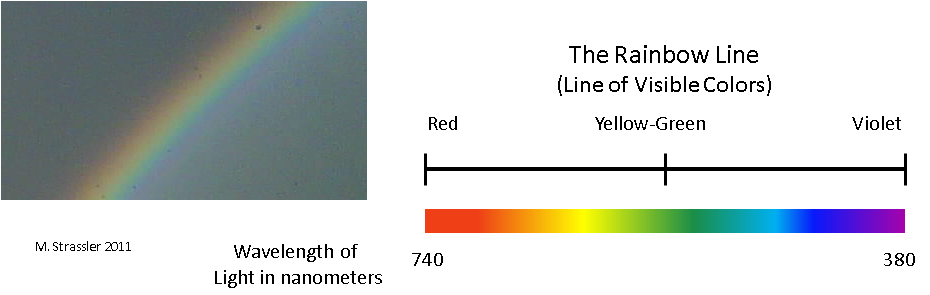 Fig. 2
Fig. 2This is obviously not a measurement of physical space either! You can throw a ball from your house to your neighbor's house, but you cannot imagine how you throw a ball from green to orange — this does not make sense. Still, it will also be a measurement. Here you can ask many meaningful questions: how does the color of the apple move along the rainbow line in the process of turning an apple from green to red? How many sunshine does each color have? If the orange star begins to turn red, will it turn yellow at first?
Wind direction measurement
But the third measurement option, and again another. If you listen to the weather forecast, you will be told that the wind will soon start to blow from the north, or from the north-west, or from the south-west. Possible wind directions are also measurement. Please note that this is not a spatial dimension! In this dimension, you can not throw the ball as you throw it up, left or forward. This is a measurement of directions in space!
 Fig. 3
Fig. 3How can you imagine this measurement? There are at least two natural methods for this, shown in fig. 3. One uses a segment — the “eolian line” (
Aeolus is a demigod, the lord of the air elements of the Ancient Greeks) —but the eolian line differs from the rainbow line in its periodicity. Wind direction may change from north to east, then to south, then to west, and then again to north, continuously. And in our view, the line can be cut anywhere - compare the two lines at the top of fig. 3, which equally well represent the eolian line. The bottom line is that the wind can go from the right end of the line right to the left end, and vice versa, so no matter where it is cut. Or perhaps it is easiest to represent this periodic line as a circle. This is what we do with a compass or weather vane!
Three different one-dimensional worlds
And here's one-dimensional worlds. See how rich they are in details! Different sizes, different properties. On the income line, income can grow or shrink forever. On the rainbow line, your eyes can only move to purple, or to the other side, only to red. And on the aeolian line the wind can make a full circle as long as necessary - but at the same time it will always return to one of the directions.
These varieties of one-dimensional worlds — infinite, finite, and finitely periodic, represented by an infinite line, segment, and a circle — are the basic ingredients for understanding worlds of higher dimensions. I will refer to them again and again. In fig. 4 they are presented, as well as the fourth type, which extends infinitely only in one direction. An example of such a measurement can be temperature: it can be arbitrarily large, but there is the lowest possible temperature — absolute zero — so the temperature forms a line starting at absolute zero and going from there upwards, but not downwards.
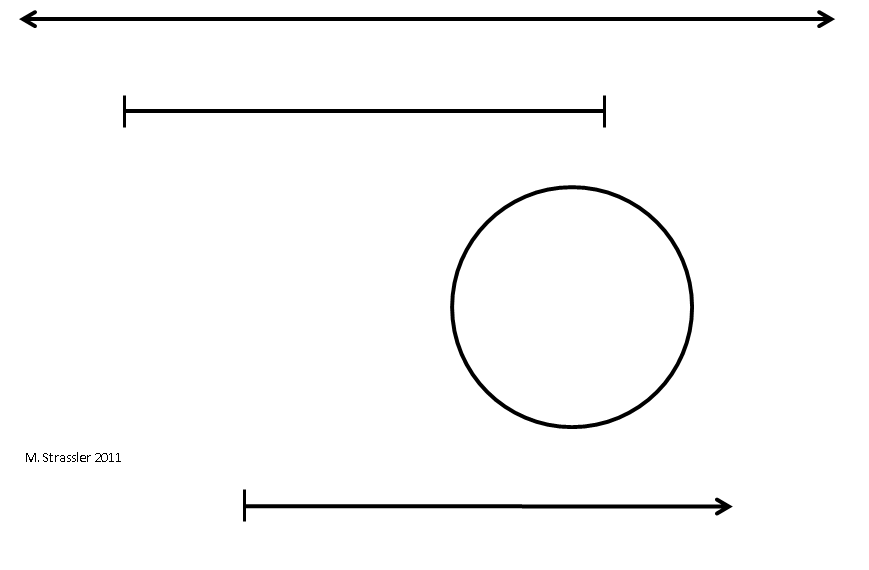 Fig. four
Fig. fourHow to depict measurements, spatial and other
I casually mentioned or used several different methods of representing measurements. Revenue can be represented by a number or an infinite line. The visible rainbow can be represented as a segment, or as a color, as well as using a number — the wavelength of the photons corresponding to a specific color. The wind direction can be represented by a circle, or a segment, whose left end is connected to the right - or words like north, east, south, west - by a number defining the direction in degrees, going from 0 to 360 and back to 0. What we can presenting one dimension in many different ways gives us tremendous flexibility to train intuitive work with additional dimensions.
To illustrate these types of dimensions, I chose concepts that were not related to physical space — income, rainbow color, wind direction — to show that spatial dimensions are concrete examples of a more general concept of measurement. Understanding this fact greatly facilitates attempts to present worlds with more than three dimensions. Remember, I mentioned two parts of the process of learning to think about additional dimensions? First, learn to represent them; secondly, understand how everything works and works in them. Spatial dimensions have features related to how some things work in them, but not with their presentation.
Spatial worlds with one effective dimension
Given all this, we will consider the spatial worlds that we regularly encounter with one effective dimension. Or, more precisely, such situations in which a certain aspect of our world behaves as if space has only one dimension. Then we say that the world for certain participants or objects becomes effectively one-dimensional.
 Fig. five
Fig. fiveImagine a tightrope walker balancing on a high rope. The world of the ropewalker is effectively one-dimensional (although it, of course, actually remains three-dimensional), since it is not able to safely move in any direction other than from right to left or left to right. This world is like a rainbow world - it is finite in length, and when the ropewalker reaches the end, he has to turn around and go back (or leave the rope, ending a situation in which the world becomes effectively one-dimensional). What more can be said? The position on the rope can be determined by one unit of information (for example, the distance from the left pole to the rope walker). Two tightrope walkers can meet on the same line, but do not pass by each other.
We can turn the rope world into an eolian line, closing it into a circle (Fig. 6). In it, two rope walkers, too, could not pass by each other - this is the main feature of one-dimensional worlds. And that would still be the final dimension. But the tightrope walker in such a situation could already walk in a circle continuously and endlessly, without stopping.
 Fig. 6
Fig. 6Other one-dimensional worlds known to us (effectively):
- Narrow road - one-dimensional world for cars;
- A narrow path with a cliff is for a tourist climbing uphill;
- The floors of the high-rise building - for the elevator.
In general, the world remains three-dimensional, but to describe a car, a tourist or an elevator, only one dimension needs to be presented.
Further remember: we live in the seeming three-dimensional world, and everything that we meet, it seems to us three-dimensional. But sometimes our three-dimensional world (more precisely, its part) can behave as effectively one-dimensional, or two-dimensional (can you think of examples?) Or even zero-dimensional! (Anyone who is unlucky to ever get stuck in a traffic jam that does not move anywhere, knows what this world has with zero measurements!) This intuition will later be very useful to us.