In an
article on one-dimensional worlds, I wrote about various one-dimensional worlds (income line, rainbow line, aeolian line) - and all of them did not have physical dimensions of space. What is the difference between measurement in general and an honest spatial dimension? That is, what is meant when they say that measurement is somehow related to physical space?
This is to some extent an elementary question with an elementary answer, and some of you who feel familiar with such concepts may be bored. But one of the interesting facts is that the obvious answer, which will be given in this article, in the more complicated case will not be entirely true. And when we get to the wonderful topic of how quantum field theory and quantum string theory are interconnected, we will see that this answer will not be enough, and for a very clever reason. So read this, but do not dismiss as too obvious - because in the future there may be completely unobvious things.
It is probably best to understand this topic in comparisons and contrasts. Take the rainbow line (Fig. 2 from the article on one-dimensional worlds). What makes it non-spatial?

Fig. one
Suppose I have two flashlights capable of emitting light with a custom color. Each color can be represented by a dot on the rainbow line. In fig. 1 I presented the light of a black lantern with a black dot on a rainbow line, and a white dot - a white dot. Suppose a black flashlight emits green light, and a white one - blue. Now take a white flashlight and gradually adjust its color until it starts to shine yellow, as shown in fig. 1. At some point, the two lanterns will have the same color of the emitted light - the points on the rainbow line will converge. Will anything happen at this moment? Obviously not. When two points converge on the rainbow line, it does not have any physical effect on any of the flashlights. Points can pass through each other without collision, and not even exchanging greetings.
Compare this with what happens if, as in fig. 2, I will leave the colors alone, but I will try to move the white flashlight to the left, or the black one to the right. Obviously, when they get too close, they will collide - noise will occur, both flashlights will collide, and possibly damage, and their movement will change. This will happen even though they are represented by different points on the rainbow line!
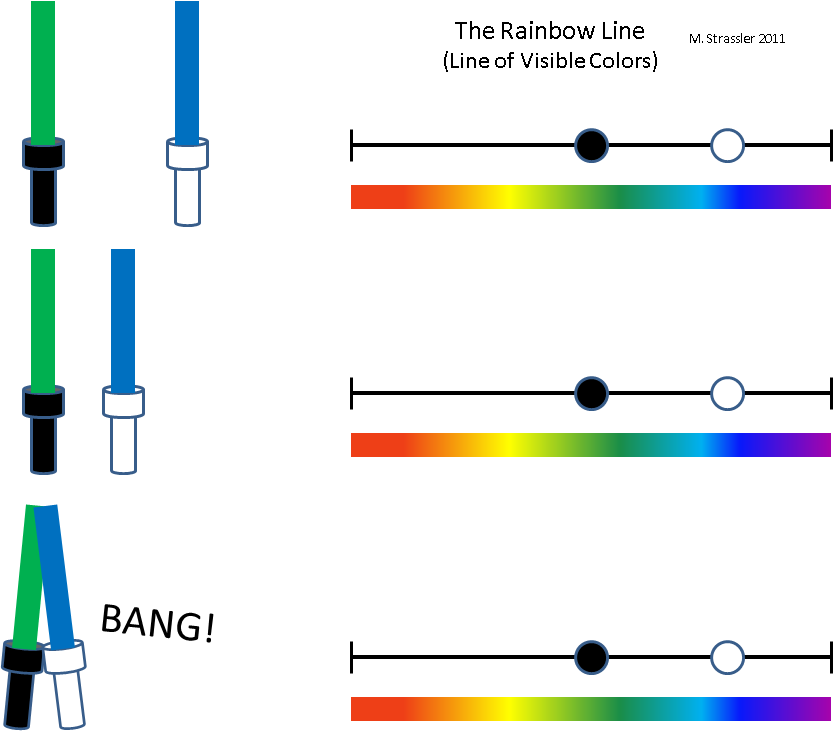
It is intuitively clear that the space in which the lanterns are located, as physical objects, is physical. In physical space there are concepts of near and far, and there are consequences of convergence. Two objects located far from each other in the physical dimension will not affect each other in the same way as two close objects. At least two close objects will be attracted by gravity more than if they were far away. If these objects are as we imagine “solid” objects, then the electrical forces inside their atoms will prevent them from passing through each other. There are no analogies to these effects due to the fact that they emit light of the same color, does not exist. Although the rainbow line is a measurement useful for representing the color of the emitted light, nothing important happens in it.
Another example: two people with different incomes can be represented as two points on the income line. If one of them gets an increase and overtakes the second, then it can affect them psychologically, but not physically! However, two rope walkers on the wire (Fig. 5 in the article on one-dimensional worlds) cannot get around each other; this is physically impossible because of the forces arising as they approach each other. In other words, you can kick someone, even if he earns 100 times more money, but you cannot kick a person 100 km away from you, even if he earns as much money as you do.
In the physical spatial dimension, concepts close and far are extremely important, more important than they can be for measurements of a more general sense. More formally, physicists call this the property of the fact that physical effects occur locally in space.
There are many subtleties associated with this concept that deserve a separate article. For example, quantum mechanics significantly complicates and enriches this concept, but does not reject it. Moreover, this is not all: there are other things that contribute to making the measurement physical. But for now this will be enough.
I so seriously approached such a seemingly simple concept, because when people talk about additional dimensions that can appear at the Large Hadron Collider, they mean additional spatial dimensions - sharing with dimensions that we can see, a feature of that measurements physical effects are local. This is not just some additional dimension of another variety. And it is very important to predict the effects of the presence of these measurements in experiments!
One non-expert asked me if thought could be considered a measurement. Another said that he believes that emotions are just as important for people's lives as space and time. And these statements are not false; the psychologist could describe some aspects of thoughts or emotions as occurring in some dimension. But it must be remembered that these measurements are qualitatively different from the physical measurements that physicists are talking about. We can think with you one thought, share one emotion, without hurting each other. But please, regardless of your thoughts or feelings, I would be very grateful if you avoided stepping on my foot!