Scientists and engineers can profitably use the long-abandoned approach to computing.
 This analog mechanical computer was used to forecast tides. He was known as the “old brass brain,” or, more formally, “The tide prediction machine # 2.” She served as the Coastal and Geological Survey of the United States for calculating tide tables since 1912, and did not retire until 1965 when she was replaced with an electronic computer.
This analog mechanical computer was used to forecast tides. He was known as the “old brass brain,” or, more formally, “The tide prediction machine # 2.” She served as the Coastal and Geological Survey of the United States for calculating tide tables since 1912, and did not retire until 1965 when she was replaced with an electronic computer.When Neil Armstrong and Buzz Aldrin descended on the moon in 1969 as part of the Apollo 11 mission, this was probably the greatest achievement in the engineering history of mankind [not counting, of course, the launch of the first satellite and the first man into space space, as well as the creation of an automatic spacecraft reusable / approx. trans.]. Many people do not realize that the important ingredient in the success of the missions of Apollo and their predecessors were the analog and hybrid (analog-digital) computers that NASA used for simulations, and in some cases, even for flight control. Many of the people living today have not even heard of analog computers, considering that computers, by definition, are digital devices.
If analog and hybrid computers were so valuable half a century ago, why did they disappear almost without a trace? This is due to the limitations of the 1970s technologies: in fact, they were too difficult to develop, build, manage, and maintain. But analog and hybrid analog-digital computers built with the help of modern technologies would not have such flaws, so now there are numerous studies on analog computing in the areas of machine learning, machine intelligence and
biomimetic circuits.
In the article, I will focus on another application of analog and hybrid computers: effective scientific computing. I believe that modern analog computers can complement their digital colleagues in solving equations related to biology, fluid dynamics, weather prediction, quantum chemistry, plasma physics, and many other areas of science. And that's how these unusual computers could do it.
An analog computer is a physical system that is configured to operate according to equations that are identical to what you want to solve. You assign initial conditions corresponding to the system you want to explore, and then you allow variables in an analog computer to evolve over time. As a result, you get a solution to the corresponding equations.
Let's take, to the point of absurdity, a simple example: a hose with water and a bucket can be regarded as an analog computer that performs integral calculations. Adjust the amount of water flowing in the hose to match the function you are integrating. Direct the flow into the bucket. The solution will be the amount of water in the bucket.
And although some of the analog computers actually used flowing fluids, the earliest of them were mechanical devices containing rotating wheels and gears. They include the 1931 Vannevar Bush differential analyzer, based on principles born in the 19th century, mainly based on the work of William Thomson (who later became Lord Kelvin) and his brother James, who developed mechanical analogue computers for calculating tides. Analog computers of this type were used for a long time for such tasks as controlling guns on battleships. By 1940, electronic analog computers began to be used for this, although in parallel, mechanical computers continued to remain in service. And none other than Claude Shannon, the father of formal information theory, published in 1941 a fruitful theoretical study of analog computing.
Around that time, extensive development of analog computers began in the USA, USSR, Germany, Britain, Japan, etc. They were produced by many manufacturers, for example, Electronic Associates Inc., Applied Dynamics, RCA, Solartron, Telefunken and Boeing. Initially they were used in the development of shells and aircraft, as well as in flight simulators. Naturally, the main client was NASA. But their use soon spread to other areas, including the management of a nuclear reactor.
 This electronic analog computer, PACE 16-31R, manufactured by Electronic Associates Inc., was installed at the Lewis Jet Flight Laboratory at NASA (now the Glenn Research Center) in Cleveland in the mid-1950s. Such analog computers were used, among other things, for such comic programs by NASA as Mercury, Gemini, Apollo.
This electronic analog computer, PACE 16-31R, manufactured by Electronic Associates Inc., was installed at the Lewis Jet Flight Laboratory at NASA (now the Glenn Research Center) in Cleveland in the mid-1950s. Such analog computers were used, among other things, for such comic programs by NASA as Mercury, Gemini, Apollo.Initially, electronic analog computers contained hundreds or thousands of electron tubes, which were later replaced by transistors. At first they were programmed by manually setting contacts between different components on a special panel. They were complex and fancy machines, they needed specially trained personnel to start up - all this played a role in their demise.
Another factor was the fact that by 1960 digital computers were developing by leaps and bounds due to many of their advantages: simple programming, algorithmic work, simplicity of storage, high accuracy, the ability to handle tasks of any size with time. The speed of digital computers quickly increased over the decade, as well as the next, when MOP (metal oxide semiconductor) technology was developed for integrated circuits, which allowed to place a large number of transistors operating with digital switches on a single chip.
Manufacturers of analog computers soon incorporated digital circuits into their systems, which gave rise to hybrid computers. But it was already too late: the analog part of these machines could not be integrated on a large scale using the technology of development and production of that time. The last major hybrid computer made in the 1970s. The world switched to digital computers and never looked back.
Today, analog MOS technology is extremely advanced: it can be found in the receiving and transmitting circuits of smartphones, in complex biomedical devices, in all consumer electronics, and in many smart devices that make up the Internet of things. Analog and hybrid computers built using such advanced modern technology could be very different from those that existed half a century ago.
But why consider analog electronics as applied to computing? The fact is that ordinary digital computers, albeit powerful ones, may already be approaching their limit. Each digital switching circuit consumes energy. Billions of transistors on a chip, switching at gigahertz speeds, generate a tremendous amount of heat, which must somehow be removed before it reaches a critical temperature. YouTube is easy to find videos demonstrating how to fry an egg on some modern digital computer chips.
Energy efficiency is especially important for scientific computing. In a digital computer, the passage of time must be approximated using a sequence of discrete steps. When solving certain complex differential equations, it is necessary to use extremely small steps to ensure that the solution is obtained as a result of the algorithm. This means that it takes an enormous amount of computation, which is time-consuming and energy-consuming.
About 15 years ago, I wondered: can an analog computer, developed with the help of modern technology, offer something valuable? To answer this question, Glenn Cowan [Glenn Cowan] - then a graduate student, whom I supervised in British Columbia, and now - a professor at the University of Concordia in Montreal - developed and created an analog computer on a single chip. It contained analog integrators, multipliers, function generators, and other blocks arranged in a
user -
programmable gate array style. Various blocks were connected by a sea of wires, which could be configured to create contacts after the chip was manufactured.
 Many scientific problems require solving systems of coupled differential equations. For simplicity, we consider two equations with two variables x 1 and x 2 . An analog computer finds x 1 and x 2 using a circuit in which the current through the two wires obeys the same equations. When using a suitable circuit, the currents in the two wires will represent the solution to the original equations.
Many scientific problems require solving systems of coupled differential equations. For simplicity, we consider two equations with two variables x 1 and x 2 . An analog computer finds x 1 and x 2 using a circuit in which the current through the two wires obeys the same equations. When using a suitable circuit, the currents in the two wires will represent the solution to the original equations. This requires analog integrators, branching units, DC sources (the summation of currents requires a simple connection of wires). To solve nonlinear differential equations, an analog computer on a chip uses continuous time circuits to form blocks capable of creating arbitrary functions (pink)
This requires analog integrators, branching units, DC sources (the summation of currents requires a simple connection of wires). To solve nonlinear differential equations, an analog computer on a chip uses continuous time circuits to form blocks capable of creating arbitrary functions (pink)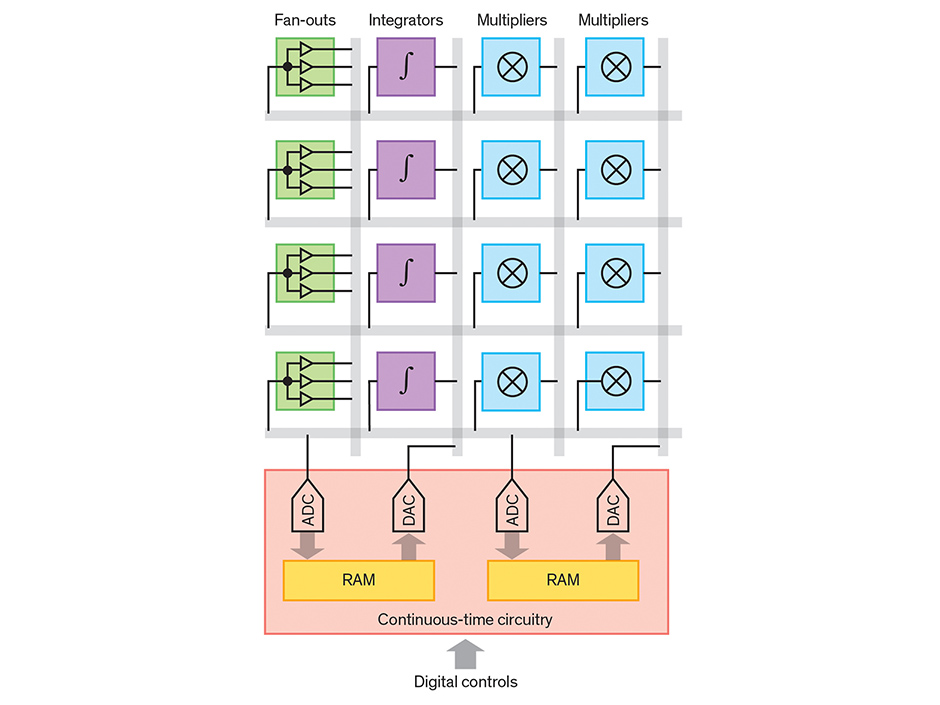 It turns out that an analog general-purpose computer can be created on the basis of a user-programmable gate array containing a number of analog elements operating under digital control. Each horizontal and vertical gray bar indicates several wires. When higher accuracy is required, the results of an analog computer can be fed to a digital computer for clarification.
It turns out that an analog general-purpose computer can be created on the basis of a user-programmable gate array containing a number of analog elements operating under digital control. Each horizontal and vertical gray bar indicates several wires. When higher accuracy is required, the results of an analog computer can be fed to a digital computer for clarification.Digital programming allowed us to combine the input of a given analog block with the output of another, and create a system controlled by the equation to be solved. The timer was not used: voltage and currents developed continuously, rather than in discrete steps. Such a computer could solve complex differential equations with one independent variable with an accuracy of the order of several percent.
For some applications, this limited accuracy is enough. In cases where such a result is too rough, it can be fed to a digital computer for clarification. Since the digital computer starts with a very good guess, the final result can be achieved in a time 10 times less, which also reduces power consumption by the same amount.
Recently, in British Columbia, two students, Ning Guo [Ning Guo] and Yipeng Huang, Mingoo Seok, Simha Sethumadhavan, and I created an analog computer on a second generation chip. As in the case of early analog computers, all units of our device worked simultaneously, and processed the signals in a way that would require a parallel architecture from a digital computer. Now we have larger chips consisting of several copies of our second generation design, capable of solving larger problems.
The new circuit of our analog computer is more efficient in energy consumption and it is easier to pair with digital computers. The advantages of both worlds are available to such a hybrid: analog for approximate calculations with high speed and low power consumption, and digital for programming, storage and high-precision calculations.
Our latest chip contains many contours used in the past for analog computing: for example, integrators and multipliers. A key component of our new scheme is the new contour capable of continuously calculating arbitrary mathematical functions. And that's why it matters.
Digital computers operate with signals that accept only two types of voltage levels, representing values of 0 or 1. Of course, when switching between these two states, the signal must also take on intermediate values. A typical digital circuit processes signals periodically, after the voltages have stabilized at levels clearly representing 0 or 1. These circuits operate using a system timer with a period sufficient for the voltage to switch from one stable state to another before it starts the next round of processing. As a result, such a scheme produces a sequence of binary values, one at a time.
Our function generator instead works with our developed approach, which we call the digital continuous time process. In it appear timeless binary signals that can change the value at any time, and not at a clearly defined clock. We built converters from analog to digital and from digital to analog, as well as digital memory capable of processing such digital signals of continuous time.
We can feed an analog signal to such a converter from analog to digital, and it will convert it to a binary number. This number can be used to find the value stored in memory. The output value is then fed to the digit-to-analog converter. The combination of such continuous-time circuits provides a function generator with analog input and output.
 The author and his colleagues used modern production technologies to pack a powerful analog computer into a small case.
The author and his colleagues used modern production technologies to pack a powerful analog computer into a small case.We used our computer to solve various complex differential equations with an accuracy of a few percent. This can not be compared with a conventional digital computer. But accuracy is not everything. In many cases, approximate values are sufficient for operation. An approximate calculation - an intentional limitation of the accuracy of calculations - is sometimes used in digital computers, for example, in areas such as machine learning, computer vision, bioinformatics and big data processing. This makes sense when, as is often the case, the input data itself has errors.
Since the core of our computer is analog, if necessary, it can directly connect to sensors and power drives. High speed allows it to interact with the user in real time in computing tasks that would normally be extremely slow.
Of course, our approach to computing has flaws. One of the problems is that especially complex tasks require a multitude of analog computing units, which is why the chip is large and expensive.
One of the ways to solve this problem is to divide the computational problem into small subtasks, each of which will be solved by an analog computer running digital. Such calculations will no longer be completely parallel, but at least they will be possible. Researchers studied this approach several decades ago, when hybrid computers were still in vogue. They did not go far, because this kind of computers was abandoned. So this technology requires further development.
Another problem is that it is difficult to configure arbitrary connections between remote circuit blocks on a large analog chip. A network of contacts may acquire prohibitively large size and complexity. However, some scientific problems will require such connections so that they can be solved on an analog computer.
This limitation can help circumvent the three-dimensional production technology. But so far the analog core of our hybrid design is best suited for those cases where local connectivity is required - for example, to simulate a set of molecules that interact only with molecules that are close to them.
Another problem is the difficulty in implementing the functions of many parameters and the related problem of low efficiency of processing partial differential equations. In the 1970s, several technologies were being developed to solve such equations on hybrid computers, and we plan to start from where the earlier developments ended.
Also, the analog has disadvantages with increasing accuracy. The accuracy of the digital circuit can be increased simply by adding bits. Increasing the accuracy of an analog computer requires the use of a much larger chip area. That is why we focused on applications with low accuracy.
I mentioned that analog computing can speed up calculations and save energy, and I want to add more details. Analog processing on a computer of the type that we did with colleagues usually takes one millisecond. Solving differential equations with one derivative requires less than 0.1 µJ of energy. Such a chip with a conventional production technology (65 nm CMOS) will occupy an area the size of a square millimeter. Equations with two derivatives take twice as much energy and chip area, and so on; the time for their decision remains unchanged.
For some critical applications with an unlimited budget, you can even consider the integration of the scale of the substrate - the entire silicon substrate can be used entirely as one giant chip. A 300 mm substrate will allow more than 100,000 integrators to be placed on the chip, which will allow simulating a system of 100,000 paired nonlinear dynamic equations of the first order, or 50,000 of the second order, and so on. This may be useful for simulating the dynamics of a large array of molecules. Decision time will still be calculated in milliseconds, and energy dissipation - tens of watts.
Only experiments can confirm that computers of this type will be really useful, and that the accumulation of analog errors will not prevent them from working. But if they make money, the results will surpass everything that modern digital computers are capable of. For them, some of the complex tasks of this order require huge amounts of energy or time to solve, which can stretch for days or even weeks.Of course, in order to find answers to these and other questions, a lot more research will be needed: how to distribute tasks between the analog and digital parts, how to break big tasks into small ones, how to combine final solutions.In search of these answers, we and other researchers engaged in analog computers can get a big advantage by taking advantage of the work of very intelligent engineers and mathematicians, which was done half a century ago. We do not need to try to reinvent the wheel. We should use the results obtained earlier as a springboard, and move much further. At least, we hope so, and if we don’t try, we’ll never know the answer.Janis Tsividis - Professor of Electrical Engineering at Columbia University