I have already
given you
several examples of how
additional dimensions can be represented in nature - dimensions in space, which we are not aware of. But so far I have not yet explained how scientists can learn about their existence.
Here you can use several basic strategies, but for now I will focus on one simple consequence of the existence of additional dimensions. It is very general in nature and leads to a strategy for studying particle physics that is relevant to many studies, including experiments at the Large Hadron Collider.
My explanation will go in two stages. At the first stage, with the help of the simplest physics, I will give you an intuitive understanding, simple but imperfect (since it will not take quantum mechanics into account), and will provide a partially incorrect answer. In the second step, I will correct the inaccuracy, which will require another additional complication, and then you will see the entire answer.
But before you begin the explanation, I will first give you an answer right away so that you understand that I will need to explain to you. Here it is - in several versions, so that you can understand.
Any particle moving in dimensions that are additional to those already known to us will seem to us, naive observers who have no idea about additional dimensions, particles of several types, each of which moves only in dimensions known to us, and the differences between them very small, except for their masses.
In other words: if a particle of a certain type can move in all dimensions, then to an uninformed observer it will seem that in nature there is not only this particle (moving only in measurements known to it), but a whole set of accompanying particles, “KK-partners”, each of which also moves in known directions, slightly different from the original particle, except that they will be heavier. “KK” denotes the
Kaluza-Klein theory , which will be discussed later.
Suppose we live in four spatial dimensions, three of which are large (known to us), and the fourth is very short (such as the width of the strip, which I used in the previous examples). By short is meant a really short distance, smaller than the diameter of a proton. Let's call this distance L.
Now imagine that there is a particle, very, very small, smaller than L, which can move freely in all four spatial dimensions. We also assume the existence of clever observers who know that this particle can move in four dimensions and has a mass m. Now consider the naive observers, us who are not aware of the small spatial dimension, who believe that they live in a three-dimensional world. After some experiments indicated in fig. 1, we can say: “here is one type of particle that can move in three dimensions, and it has mass m; but look, another type of particle, also capable of moving in three dimensions, and it is similar to the first, only its mass M is much larger than m; and, wow, here is another type of particle capable of moving in three dimensions, similar to the first, only it has a mass M ', more than M; and one more type of particle, mass M "; and more and more ... "
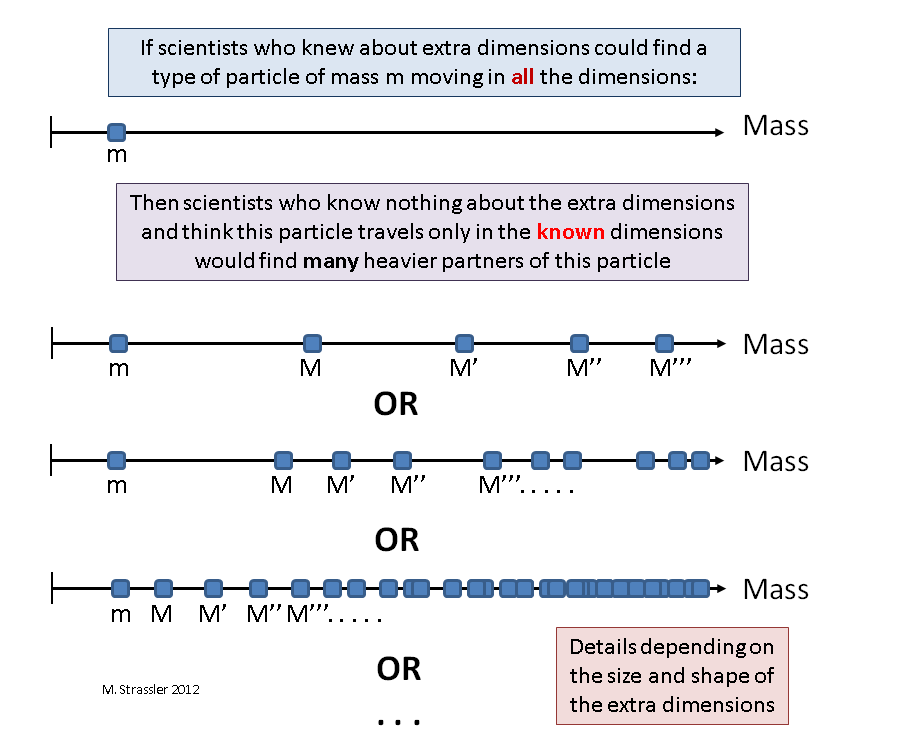 Fig. one
Fig. oneThe masses M, M ', M ”and so on determine the combination of the fundamental mass m and the geometry of the additional spatial dimensions - in particular, M, M', M” and so on are inversely proportional to L. The smaller L, the larger M, M ', M ”and so on, and the more difficult it is to find heavy KK-partners. Moreover, the sequence of masses appearing in KK partners gives a direct indication of the number, size and shape of the additional dimensions. You can give a musical analogy - this fact is due to the fact that the exact harmonics produced by the instrument can give information about its shape and size.
For example: if photons could move in one or several additional dimensions, like a boat in a channel, then an observer who would be aware of additional dimensions would describe them as massless particles (m = 0) moving in all dimensions . But a human scientist, who so far only knows a massless photon moving in three known dimensions, would discover a set of heavy particles similar to photons. The smaller the size of the additional measurement, the greater the mass of KK photons, and the more difficult it is to open them - the more precisely, the heavier they are, and the more energy the particles accelerator will need to generate them.
It may well be that several types of particles can move in additional dimensions, in which case scientists will open heavy KK partners for each of these types of particles (see Fig. 2). The discovery of a small number of heavy particles that resemble some of the known light particles, whose mass distribution will show similar to Fig. 2 distribution will clearly indicate that new particles are KK-partners, and that we have one or several additional dimensions.
 Fig. 2
Fig. 2This is the simple answer: a particle moving both in additional dimensions and in known dimensions will reveal itself to us through the detection of its heavy KK partners. Later I will describe more precisely how you can try to produce and open KK partners in the experiment. In the
following articles, I will describe why this particular answer would be the right one - and I will give a simple and complex explanation.