 Fig. 1: a small boat in the canal can move up and down
Fig. 1: a small boat in the canal can move up and downIt's time to learn something with the help of
two-dimensional space that we could not find out using
one-dimensional . In particular, let us turn to a strip — a space that looks like a ribbon, with one very long dimension (perhaps infinite), and one very short. Much of what belongs to the strip will be true for the pipe, but I will limit myself to a strip, since it is easier to draw.
First, let me remind you of the concept I introduced at the end of the
article on one-dimensional worlds . Even if a physical world is three-dimensional, for example, our familiar world is with you, for certain aspects of it it is possible to behave as if they are one-dimensional. For example, a person walking along a rope exists in three dimensions, but his movements will be essentially one-dimensional. In this case, his world makes one-dimensional restrictions necessary for its security. On the strip, we have one more reason why this world can be effectively one-dimensional. It has a large dimension and a small one, and whether you can move along a small one depends on your shape and size compared to the distance describing the small dimension.
Here is an example of a strip: the shipping channel. A long strip of water allows the small boat to move in two dimensions: it can move up and down through the channel, or across it, back and forth. But a giant cargo ship, barely placed in a canal, is only able to move forward or backward. For a cargo vessel, the channel is effectively one-dimensional. If you watched his movement, you would not find signs of a two-dimensional channel. The movement of a large object — large compared to the width of a strip — reveals a long measurement for us, but shows no signs of a second, short one; the second dimension is opened only by the movement of a small object, such as a small boat. This is a very important lesson!
 Fig. 2: A giant cargo ship can only move forward and backward along the canal.
Fig. 2: A giant cargo ship can only move forward and backward along the canal.Another example of the same? For us, the surface of a human hair is, in fact, a one-dimensional object, if you look at it with the naked eye. Hair can be cut into two pieces in half the length, but it will be very difficult for us to cut the hair along: in English there is even such a thing as “splitting hair”, meaning an activity that is not worth the time and effort. But a tiny dust mite is able to crawl along the surface of the hair as if it were a giant pipe. For a tick, the surface of the hair appears to be two-dimensional, just as for us the surface of the flagpole looks two-dimensional.
Returning to the cargo ship. Imagine that this vessel would be a rational being, with a brain that receives information from the sense organs, as it does in animals, but with a single sense organ that allows it to determine only its own movement.
Why do I appeal to consciousness? It does not matter for the spatial dimensions that we are discussing - they are regardless of whether the vessel has a consciousness or not. I am trying to explain to you how a rational being - such as you - can be misled by its senses and brain about the true properties of nature, and may not have an idea of spatial dimensions.
The only information going from such an organ of sense to the brain of a ship will be something like “forward at a speed of five kilometers per hour” or “back at a speed of two kilometers per hour” or “motionless” [on water, speed is usually measured in nodes, i.e. . nautical miles per hour; in addition, there is a difference in velocity relative to the surface of the water and relative to the bottom. But in this case it can be neglected. trans.]. What picture of the world would a ship's brain build? Without any information coming from outside about the presence of the second dimension across the strip, he naturally would have created a one-dimensional picture of the world in which the channel had one dimension. The vessel would not have information about the second dimension, although it would have been easily detected by a small boat.
 Container Ship Panama Canal
Container Ship Panama CanalThis is one example of how “extra dimensions” can work (but not the only one, as we will see later). Under the "additional" means that this dimension, the existence of which the freighter did not know and could not know, given his senses.
Now imagine that something similar applies to us. Suppose we live in a strip, which, in addition to the three large spatial dimensions, within which we usually move, which we recognize with our senses and represent in our head, there is also a fourth spatial dimension, so incredibly small that we fill it with cargo ship, and can not move in it. Moreover, our organs of sight, hearing, touch, smell, or taste are not able to detect the presence of this additional dimension. As far as our brain knows, it is not there. But maybe, in fact, it is there, and quite small creatures could move along it and feel it.
The assumption of the existence of one or several additional dimensions is merely reasoning, pure fiction. We do not know whether it is true. But I try to explain to you that we do not know that it is false.
So the next question is this: can people-scientists, whose feelings and brains are not able to distinguish the fourth dimension of space, find it? It is at this moment that the mix of human intelligence and advanced scientific instruments enters.
As we will see later, studies show that, although one or more additional dimensions of this type can exist in nature, they must be extremely small. The transverse dimension of such a measurement cannot be greater than 1/10 000 of the diameter of a proton, or 1/1 000 000 000 of the diameter of an atom, or 0.000 000 000 000 000 1 meters. Studies carried out at the Large Hadron Collider are gradually adjusted to this size.
One more example
The additional measurement example described above is only one of several common features. Here is another example. Instead of a vessel with an enormous width occupying the whole canal, we consider a narrower vessel firmly docked to one side of the canal so that although, in principle, it can move across the canal, in practice it will not work. The relationship between the boat and the additional dimension is different, but the effect of this is that the small dimension of the two-dimensional channel cannot be detected by the movement of the boat is the same.
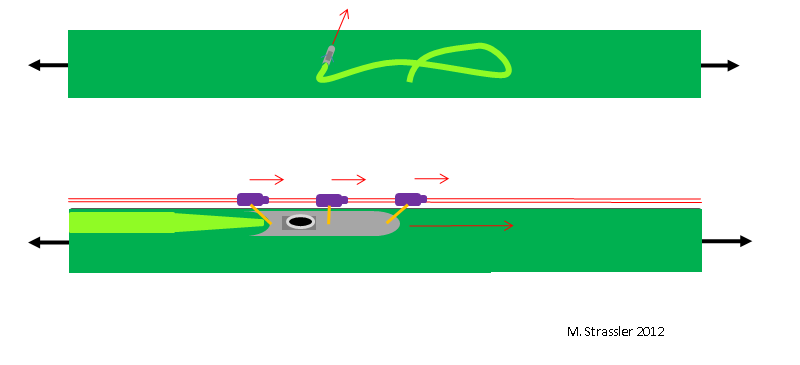 Fig. 3
Fig. 3More specifically, imagine a boat that, like in fig. 3, moving forward or backward along the canal, using both its own engine and the assistance of vehicles moving along the rails along the canal — a modern form of
shoreline . Unlike a large container ship, this boat does not fill the entire width of the channel. In principle, it could move across the channel, from one side to the other. But in practice there are forces — exerted by ropes connecting it with devices moving on rails — which hold it against the left wall of the channel. And these forces are so strong that the boat never moves away from the left wall. And since it moves forward and back along the canal, its movement is purely one-dimensional. As with a large ship, we can imagine that if this boat were conscious, and her feelings would give her only information about her movement, her brain would create a one-dimensional picture of the channel, despite the fact that if you cut the ropes, the boat could would turn and move to the center, or even to the right wall of the channel!
The same is true for us. We - more precisely, every particle that makes up our body, and everything that we can see, feel, discover with the help of modern scientific tools - can be attached by forces of extraordinary magnitude, which we cannot overcome, and about which we have no idea , to a three-dimensional wall of space with four spatial dimensions. And, since our movements are limited by a wall, and our senses register only objects limited by it in a similar way, our brain builds a three-dimensional picture of the world for us, despite the fact that in fact there is an additional dimension in our world.
Again, there is no guarantee that this is actually the case. This is all pure reasoning. But we cannot be sure that this is not the case. The only way to find out is to develop and conduct scientific experiments, whose nature I will soon explain. It turns out (as was shown, to everyone's shock and distrust, in the
famous work of 1999, authored by Nim Arkani-Hamed, Savas Dimopolus and Gia Dvali) that this additional dimension of the second type can be much more than what I described earlier - maybe as big as the width of a human hair! (In fact, when this work was written, experiments still did not prohibit additional measurements to be made up to a millimeter. But since then new ones have been carried out, and they have imposed new restrictions on this possibility.) And this is surprising. Despite all the experiments conducted with the help of microscopes and tiny electronic equipment built into our computers, we still may not be aware of the existence of an additional dimension of a small, but still macroscopic size.
More examples
When we begin to reason in a similar direction, we can find even more possibilities than the two described.
For example, there is no reason for not having more than one additional dimension. We can give an example using our ship channel - after all, if it is deep enough, we can talk about it as three-dimensional, very long in one direction, but of finite width and depth. Then we can come up with many different objects for which the channel has zero, one or two additional short dimensions, as shown in Fig. four
 Fig. four
Fig. fourThe submarine can move in the channel in three dimensions. A small boat is tied to the two-dimensional surface of the channel, and moves without having a clue that the channel has depth [in reality, to the boat skipper, who has no idea about the depth of the channel, various questions arise / approx. trans.]. Her two-dimensional perception of the world does not take into account one additional dimension. And three different types of ships will not be aware of two of the three dimensions. One example is a boat in tow tied to a wall and surface. Another example is a wide barge that fills the channel to its full width and is attached to the surface. And, finally, the third example is a gigantic ship, reaching the keel of the canal, and, in fact, filling it entirely. For three completely different reasons, the movement of these three vessels would show no signs of the depth and width of the channel, and if they were thinking beings, they might be surprised to learn that there are two additional dimensions in their world.