In the
previous article, I explained why naive observers who are not aware of the presence of an additional dimension, it would seem that a particle capable of moving in additional dimensions has Kaluza-Klein's partners (KK), heavier versions of the original particle. I pointed out that when the primordial particle of mass m moves in the direction of an additional dimension, to the naive observer it seems stationary and heavier than it should be, that is, as if it were a particle of another type. Such a class of supposedly new particles, similar to the original, but heavier ones, is called KK-partners.
In the case of a
strip , if a particle of mass m moves across the strip with a moment p
across , the observer, who considers the strip as a line, will assume that the particle is a QC partner with zero momentum and mass M, where
Although this is generally true, it follows from this that for each mass M greater than m, there must be its own QC partner. But this is not so - our world is quantum (see Fig. 1 of the previous article). Now we find out exactly how quantum mechanics changes the whole picture.
The key feature of quantum physics that we need is that for a quantum “particle” moving in a finite size dimension, not all possible values of p
across are permissible. In a more general formulation: quantum mechanics says that a “particle” moving in a finite size measurement can have only certain values of momentum in this direction.
This is one of the most important and strange consequences of quantum mechanics! At first glance, this is completely counterintuitive, because what can prevent you from setting a “particle” with impulse p to a slight acceleration so that its impulse is slightly different from p?
What is a quantum?
You could have noticed that I started to take the word “particle” in quotation marks, because in the current context we need to distinguish the term “particle”, used to describe electrons, muons, quarks, gluons and all other known elementary particles, from the intuitive concept particles that we inherit from our experience with dust, sand, salt and gravel. It would be better to call such “particles” as an electron, photon, Quark, etc., quanta, more cunning objects. These quanta are field perturbations, they are much more like waves than particles. The best way to understand a quantum is to imagine waves. This is another important linguistic moment: saying “wave”, I do not mean something like a separate wave in the ocean breaking on the shore - I mean a sequence of waves with many crests and hollows.
An example of such waves would be electromagnetic waves, to which the light waves that are visible to our eyes also belong. Imagine that we took such a wave — for example, a laser light — and dim the light, more and more. How can it be muffled? It turns out that in our quantum world there is the dimmest possible flash of light, which we call the quantum of light, or photon. A photon is a wave of light whose wave height and intensity is the smallest possible. We owe all of these concepts and names to Einstein, who - despite all his well-known dissatisfaction with the conceptual implications of quantum mechanics - was one of the founders of this theory.
There is nothing intuitive - from my point of view - that light waves consist of quanta, since this is not manifested in any of the processes we observe directly. But our bodies, thanks to processes that we do not realize, use this fact all the time. The light of the lamp seems continuous to our brain, but our eyes actually absorb photons one by one. Moreover, I saw with my own eyes the confirmation that light consists of quanta — I know about this not only from books.
We physicists often call these light quanta "particles of light," because in many ways they behave like particles. Any photon moving in a straight line by itself has a certain energy and momentum; all photons have the same mass value (specifically, zero); the photon cannot be divided into smaller parts; photon can be emitted or absorbed only entirely. These properties roughly correspond to what our intuition would expect from particles such as grains of sand, glass beads, dust particles, etc.
But the word “quantum” is better for many reasons than the word “particle”, since some properties of quanta are similar to the properties of particles, and some are like properties of waves. A well-known example of wave behavior is a quantum way to go through two doors at the same time and interact (in the same sense that waves interact with each other and ridges with hollows mutually destroy each other) with themselves. And then we will see another example.
It must be remembered that what is carried out for a photon is also fulfilled for all known "particles." And indeed, each of them is a type of quantum - a wave of the minimum possible height in the corresponding field. Electron - quantum of electronic field. Quark - quantum of the quark field. A Z-particle is a quantum of a Z-field, and so on.
Quanta - KK-partners
It is time to find out what I promised to explain to you: why the wave nature of quanta implies that the masses of particles of QC partners take on certain values, and not all possible values, large masses m of the original “particle”. The famous physicist
Louis de Broglie , in the wake of Einstein's first ideas, for the first time clearly determined that the relationship between waves, particles and quanta implies that for a quantum there is a relationship between:
• Its impulse (a property resembling particle properties),
• And its wavelength (a property resembling the properties of waves) [and again, here the “wave” refers to a sequence of waves, and the wavelength is the distance between the crests of the waves in the sequence].
And this dependence is expressed simply: impulse = h / wavelength
h is
Planck's famous
constant , the same fundamental fundamental constant of nature as the speed of light. Planck introduced this constant in 1900, trying to unravel one mysterious physical phenomenon. This was the first step towards the quantum nature of the world. Every time you try to describe a phenomenon in which quantum mechanics plays an important role, the constant h appears. In many formulas, you can see the value of ℏ, and this is just h divided by 2π, since this value is often more convenient to simplify formulas.
 Fig. 1: consider a quantum moving along a strip and through a tube
Fig. 1: consider a quantum moving along a strip and through a tubeIn some cases, it turns out to be a little easier to explain what happens with a quantum moving through a pipe than with what moves along the strip used by us in the previous examples. Almost everything that works for a pipe will be true for a strip. Therefore, I will use them together.
The lightest KK partner
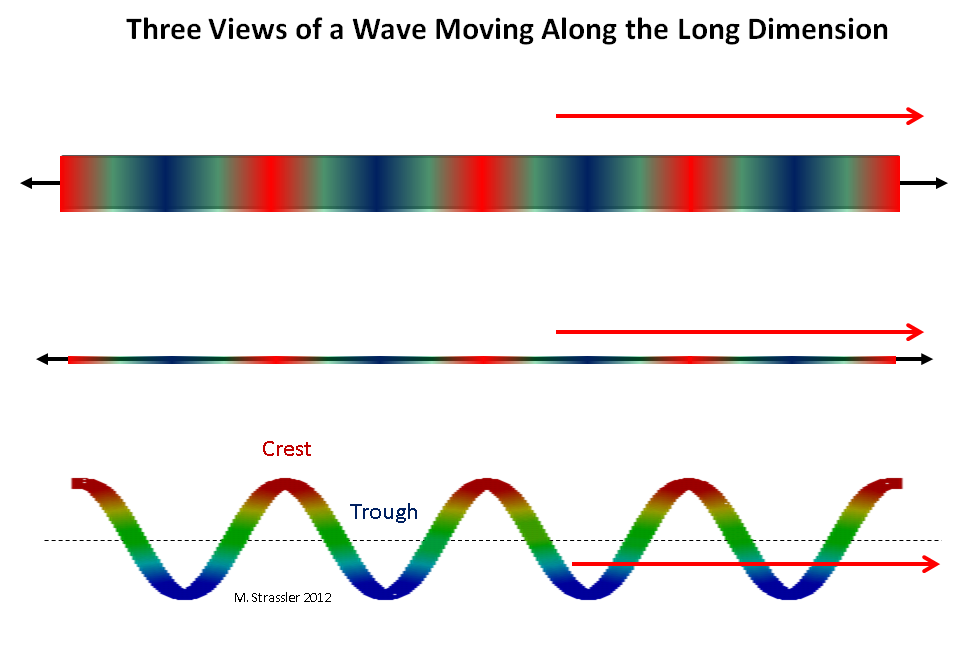 Fig. 2: three views of a wave moving along a long dimension
Fig. 2: three views of a wave moving along a long dimensionImagine a quantum traveling along a strip of width W, or along a tube of circle S. First, imagine a quantum moving along a long dimension (long means infinite, or so long that it can be infinite as far as we can judge it). A wave traveling along a strip or pipe can move along a long dimension in any direction and have any wavelength (the distance between two adjacent crests). See fig. 2. Such a quantum can have any pulse along a strip or pipe, according to de Broglie: a pulse can be zero, very small, small, large, in any direction, etc. In principle, the impulse can be made slightly larger (or slightly smaller) by pushing the quantum in the direction of its movement (or in the opposite direction).
 Fig. 3: two views of a wave moving along a short tube dimension
Fig. 3: two views of a wave moving along a short tube dimensionNow consider a quantum (i.e., a “particle”) moving across strips or tubes. First, it obviously will not be able to have a wavelength greater than the transverse distance of the strip or the circumference of the pipe! This is easy to see on the pipe: it should contain at least one ridge (red) and one depression (blue) that move along the pipe, as shown in fig. 3. If the wavelength is greater than S, the wave will not connect with itself, as shown in fig. 4. The longest wavelength will be exactly S; and a single depression of the wave should be located exactly on the side of the pipe opposite to the single ridge.
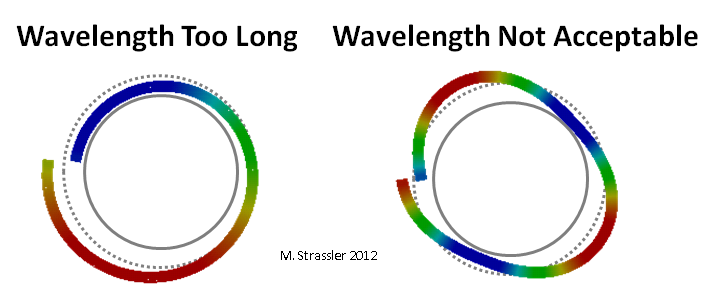 Fig. 4: unsuitable wavelengths
Fig. 4: unsuitable wavelengthsThe crest and trough of the wave in Fig. 3 move around the pipe, recalling (fig. 5) a normal non-quantum particle (here I really mean something like a grain of sand, not a quantum or "particle") rolling along the pipe, but with one important difference: if an ordinary intuitive particle is no problem may move slightly faster or slower, because of which its impulse will slightly increase or decrease, the quantum corresponding to the wave cannot have a slightly larger or smaller impulse, since this would correspond to an unacceptable wavelength (Fig. 4).
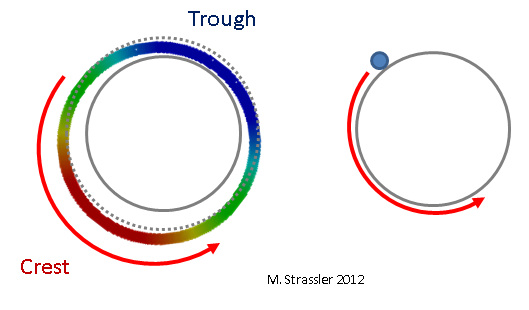 Fig. 5: the wave is like a particle
Fig. 5: the wave is like a particleOn the strip it is a little trickier, but, as shown in fig. 6, there again, there can be only one ridge at one wall and one at the other, and this position changes with time: the ridge does not move, but decreases in size and turns into a hollow, and the hollow turns into a ridge. Note that, unlike fig. 3, where the crest and trough retain their size but move along a pipe, the crest of this wave does not move, but shrinks. Therefore, it is called "standing wave". For a similar (but not identical) example, imagine a guitar or violin string. Intuitively, this standing wave corresponds to an ordinary non-quantified particle moving forward and backward across the strip. (Less intuitively, but more precisely, it corresponds to an ordinary particle moving both ways at the same time. But this very strange and cool quantum fact is not important now.) This is shown in Fig. 7
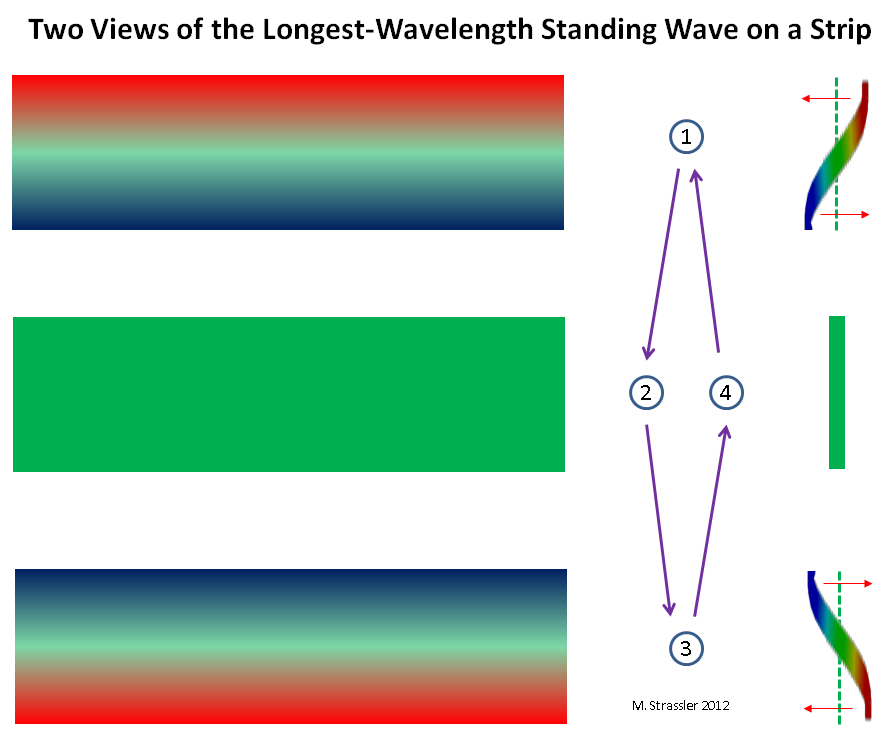 Fig. 6: two views of the standing wave with the longest wavelength
Fig. 6: two views of the standing wave with the longest wavelengthIn both cases, there is the longest possible wavelength (S for pipe, 2W for strip). This means that there is also the smallest possible impulse (h / S and h / 2 W for pipe and strip). And finally, this means that there is the lightest possible KK particle! With mass M, where
Note that for massless particles, m = 0, these formulas are reduced to:
And these latter formulas are roughly correct if S and W are very small, as is often the case in plausible reasoning.
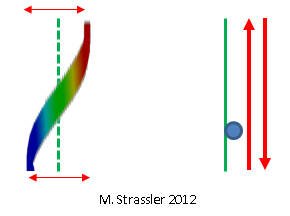 Fig. 7: the standing wave quantum is a bit like a particle moving back and forth
Fig. 7: the standing wave quantum is a bit like a particle moving back and forthAnd so we learned that, in fact, “particles” are in fact quanta, with properties resembling the properties of waves:
- In the lightest CK partner, the mass M is quite strong than m,
- Since the formulas for M include 1 / W and 1 / S, the smaller the extra dimension, the heavier the lightest CK partner.
- In fact, when S and W become so small that M greatly exceeds m (or if m is initially initially zero), then M turns out to be roughly proportional to 1 / S or 1 / W.
Fine. This is the main point, so please make sure you understand it before you continue. It remains to explain something else:
- Why are there many KK partners with different masses M, M ', M ”, etc. (where, by definition, M <M '<M ”, etc.)
- Why these masses are separated from each other.
- Why the masses grow with a decrease in additional measurement.
- Why KK partners of different types of particles capable of moving in the same additional dimension will have similar masses, especially for heavier KK partners.
- Why the masses of KK-partners will give us direct information about the form, size and number of additional measurements.
From the above, the answers can be quite easily derived.
Beyond the lightest QC partner
 Fig. 8: the wave with the closest to the longest wavelength, moving along the short measurement tube
Fig. 8: the wave with the closest to the longest wavelength, moving along the short measurement tubeWhy KK-partners a lot? Just because a quantum wave on a strip or tube can have many different wavelengths. In fig. 8, 9 and 10 you can see waves with a length of 1/2 or 1/3 of the maximum, corresponding (according to Einstein and de Broglie) with a double and triple quantum with respect to the minimum.
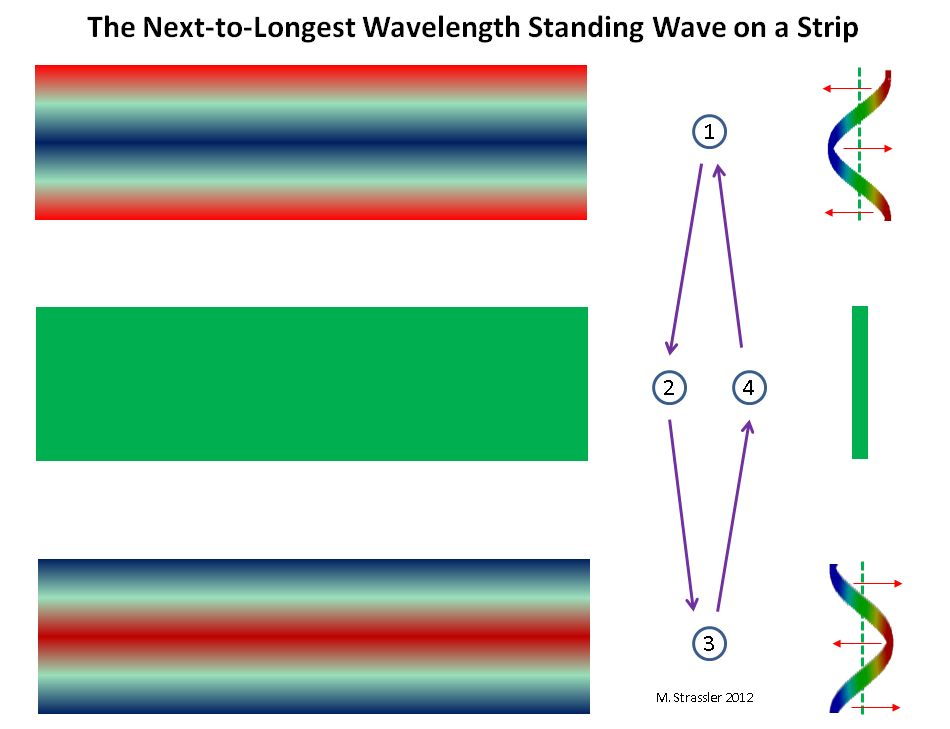 Fig. 9 standing wave with the closest to the longest wavelength on the strip
Fig. 9 standing wave with the closest to the longest wavelength on the stripSummarizing, we can say that any wavelength is allowed, which has n ridges and n cavities, where n is any positive integer (1, 2, 3, 4, ..), so that the wavelength is equal to S divided by n (or 2W divided by n) and the wave clearly fit within a circle with circle S or within a line of length W. Any other wavelength does not fit (see Fig. 4). Accordingly, taking into account the de Broglie ratio, impulse = h / wavelength, any impulse of the form nh / S (or nh / 2 W) is allowed, and for each value of n we have a CK-mass partner:
This answers almost all the questions asked, at least for cases with a tube and a strip:
- KK-partners are many (one for each n> 0),
- Their masses are well separated from each other (since when n changes by 1, M changes very much)
- Their masses grow with decreasing additional dimensions (since the last terms in the formulas become larger when W and S become smaller),
- Heavy KK partners of different particles with different masses m have similar masses M, since for sufficiently large n the second terms in the formulas are large compared to m 2 , which gives the mass of the KK partner approximately equal to M = nh / c S for the pipe and nh / 2 c W for the strip, and it almost does not depend on m.
 Fig. 10: waves on a strip and a tube with a wavelength of 1/3 maximum
Fig. 10: waves on a strip and a tube with a wavelength of 1/3 maximumThe last question remains: why the number, size and shape of additional dimensions determines the masses of QC partners - and hence, therefore, measuring the masses of a set of QC partners allows determining the properties of additional dimensions, just as listening to the sound of a musical instrument allows, in principle, determining its shape , size and materials of which it is made?
Take an extremely simplified example. Consider two additional dimensions, reusing our classic ship channel, including (as we did at the end of a
recent article with examples of additional dimensions) and the fact that the channel has depth, so we can imagine the waves inside it (waves of this type you can hear in a large room, or under water in any channel). The cross section of the channel (if we cut it at any point on the line running along a long dimension) will simply be a rectangle of width W and depth D. Just like any non-quantized particle, even being stationary from the point of view of a long dimension, can move along one or two additional measurements (and thus have a pulse either in width or in depth), so the wave will have a wavelength in both additional dimensions. Such a simple separation of the wave into what it does by measuring the width and what it does by measuring the depth is tied in a special way to the squareness of the channel, and usually will not work in other examples. For example, as shown in fig. 11, at the top, one of the allowable waves will have three cavities in the width dimension and one in the depth dimension.
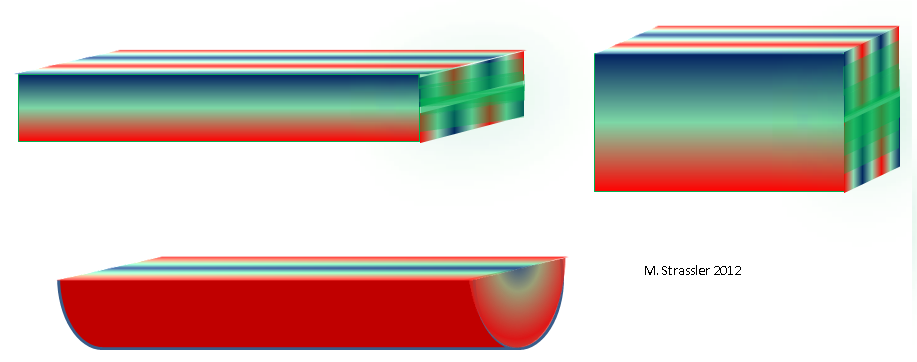 Fig. eleven
Fig. elevenWe can designate the number of cavities and ridges by measuring the width by an integer n
1 , and by measuring the depth - n
2 , and for each n
1 and n
2 (one or both of these values can be greater than zero) we get by the KK-partner. For massless (m = 0) or almost massless quanta, KK partners will have a mass
It can be seen that the mass distribution differs from the case with one additional dimension, and that it can tell us both W and D.
If the cross section of the channel will be of another shape - say, triangular or half-disk, as shown in Fig. 11, below, we will get another mass distribution, reflecting the exact shape of a triangle or half disk. And we can already discard the practical ship channels and represent the three-dimensional space, whose cross-section corresponds to any other finite two-dimensional form, one of those shown in Fig. 1
in an article about worlds with two spatial dimensions: a complete disk, or even a sphere or torus. Each of these forms will give us its own kind of mass distribution of KK-partners. And if there are three extra dimensions, or four, or five ... Perhaps many more types of distributions.
Examples of some distributions for massless particles with sizes of additional dimensions chosen so that the masses of the first CK partners are the same for each case are given in Fig. 12. Obviously, to establish the shape and size of additional measurements, it will be necessary to measure the masses of a sufficiently large number of QC partners (and even to confirm that any of the newly discovered heavy particles are generally KK partners), therefore, to understand the nature of any additional measurements, it will take time.
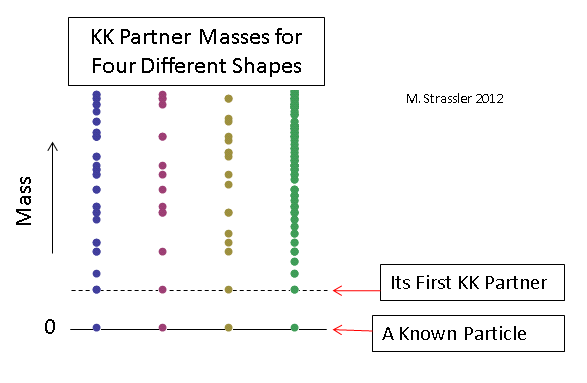 Fig. 12
Fig. 12Can the known heavy particles of matter be the lighter CK partners?
Then there is an obvious additional question. We know that among the known elementary particles there is an electron, as well as its heavier versions: muon and tau. There is an upper quark, and its heavier versions are enchanted and true. There is a lower quark, and its heavier versions, strange and charming. Are heavy particle versions of KK lung partners?
At first glance, this is a seductive assumption, but the answer to it will be a firm “no”. Excuse me. This is not at all a dumb question. It just has a clever negative answer.
Muon and tau, fascinated and true, strange and charming - they all get their masses thanks to the Higgs field, and not thanks to the impulse from the extra dimensions. This clearly follows from the detailed experiments. Clues can be found in the article on what
would have happened if the Higgs field were zero . Note that if the Higgs field was on average zero, then the electron, muon and tau would not have a mass (and each would be divided into two types of particles). This is not consistent with the theory that muon and tau are KK electron partners.
There are many other reasons. Perhaps the most serious of them is that, due to the charge of the electron and because it is surrounded by an electric field, the photon must move in any dimension in which the electron moves (although the opposite is not true). So if an electron has KK-partners, then they should be in a photon. But from our formulas (and more generalized ones like them), it follows that since the photon has no mass, and the electron mass (0.0005 GeV / c
2 ) is small compared to the muon mass (about 0.1 GeV / c
2 ), if the muon is a KK partner, then the photon must have a KK partner of similar mass. But such a particle, if it existed, would have been discovered many years ago. In fact, the KK partner photons were not observed in experiments in which masses much larger than the mass of Z particles were studied — these are many hundreds of GeV / c
2 . The Z-particle itself also cannot be a photon QC partner; she is not like him enough. And this means that any electron KK-partners must be at least as heavy.
Where to go next? To experiments
We passed from the theory (the possibility of additional measurements, related mathematics and geometry) to the predictions (CK-partners). Next step: what do we know about additional measurements from experiments? We have not yet seen QC partners in experiments, but you can ask, what can we learn from their absence? Quite a lot, as I will explain later - along with a description of how attempts to find signs of additional measurements continue at the Large Hadron Collider and in other places.