 The eight planets of our solar system and our sun, with the observance of the scale of their size, but not the scale of the orbits. The naked eye is the hardest to see Mercury. All planets move in elliptical orbits.
The eight planets of our solar system and our sun, with the observance of the scale of their size, but not the scale of the orbits. The naked eye is the hardest to see Mercury. All planets move in elliptical orbits.The best scientific theories are simple, straightforward, effectively predict the results of observations and contain internal elegance. The simplest equations of Newton F = ma and Einstein E = mc
2 contain outstanding information and allow us to derive so much from them; the models of quarks and the General Theory of Relativity are easy to describe, but these are incredibly deep theories governing particle interactions; Ideas such as supersymmetry, great unification theory, and string theory extend the well-known physics of symmetry to new levels. Applying new mathematical techniques to the Universe, we are looking for a deeper truth in reality than our current level of its understanding.
The original model of the “elegant Universe”,
Mysterium Cosmographicum [The Mystery of the Universe] Kepler was symmetrical, beautiful and based on mathematics, which was not used before. But our warning story about how it turned out to be a huge scientific failure.
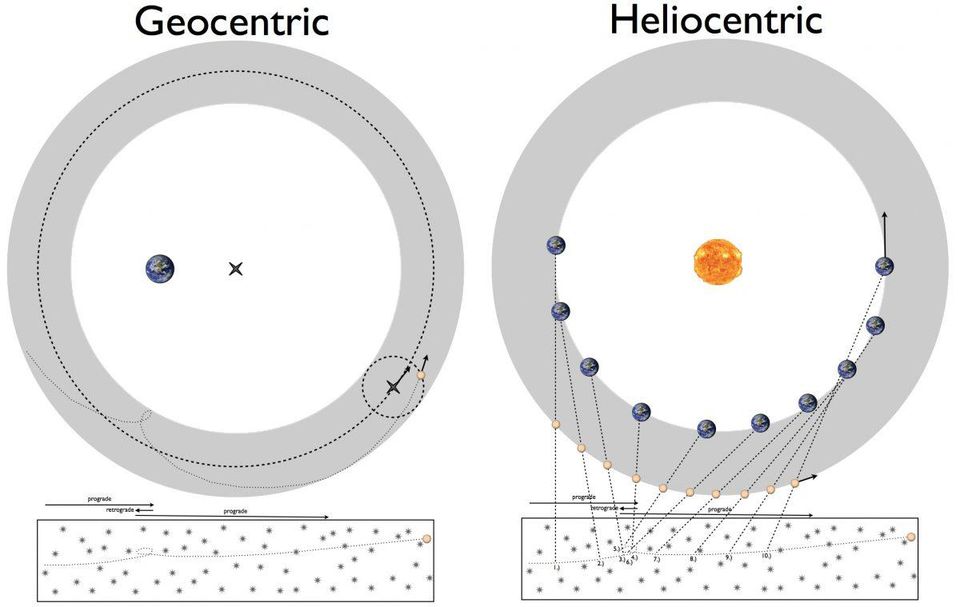 One of the greatest mysteries of the XVI century was how the planets move. This could be explained using the Ptolemy geocentric model (left) or the Copernican heliocentric model (right). However, none of them could calculate all the details with arbitrary accuracy.
One of the greatest mysteries of the XVI century was how the planets move. This could be explained using the Ptolemy geocentric model (left) or the Copernican heliocentric model (right). However, none of them could calculate all the details with arbitrary accuracy.Before Kepler, there were three main systems describing the Universe [the solar system in terms of that time]:
- The model of Ptolemy, in which the Earth was stationary, and everything revolved around it in a circle, used equants , defenders and epicycles .
- The Copernican model, in which the Sun was still and the Earth was one of six planets orbiting it, also used epicycles.
- The Tycho Brahe model, or the geo-heliocentric model, in which the Sun rotated around the Earth, and all other planets — around the Sun in circles, also using epicycles.
Kepler, creating scientific work decades before Galileo, considered heliocentric systems promising, but they needed more than just circles. To support them, an elegant mathematical structure was required. In a fit of genius, at just 24, Kepler published an idea that he considered the most beautiful of his ideas.
 Kepler decided that in the Solar System there must be exactly six planets with precisely defined orbits located on spheres inscribed in regular polyhedra.
Kepler decided that in the Solar System there must be exactly six planets with precisely defined orbits located on spheres inscribed in regular polyhedra.Since six planets revolved around the Sun (everything that is behind Saturn will be discovered only 200 years later), Kepler decided that there should be six unique orbits: one on each of the planets. But why six? Why not more, why not less? Why are there such distances between them? The connection between orbits and mathematics became his idea of an elegant universe:
I plan to demonstrate that God, creating the universe and placing the spheres, meant five regular geometric polyhedra, and limited them to the number, proportions and movement of the spheres.
You see, in three dimensions from regular polygons, you can create exactly
five polyhedra , no more and no less. They were discovered by the ancient Greeks 2000 years ago, and sometimes they are called Plato polyhedra (although they were discovered long before Plato). Kepler imagined a system of nested spheres, described and inscribed around each of the polyhedra, resulting in six spherical orbits, in which the planets move.
 Tetrahedron, hexahedron (cube), octahedron, dodecahedron, icosahedron. Five regular polyhedra, composed and regular polygons
Tetrahedron, hexahedron (cube), octahedron, dodecahedron, icosahedron. Five regular polyhedra, composed and regular polygonsThe sphere of Mercury must be the innermost, and is inside the octahedron, a regular polyhedron consisting of eight equilateral triangles. The sphere of Venus is described around it - it is also inscribed in the icosahedron, a 20-sided figure consisting of equilateral triangles. Around it is described the sphere of the Earth, inscribed in the dodecahedron, whose 12 faces are pentagons. A sphere of Mars is inscribed around it, inscribed in a tetrahedron: a tetrahedral polyhedron with sides in the form of equilateral triangles. Around the tetrahedron is described the Jupiter sphere, inscribed in a cube, the final polygon. And the last sphere is described around it, with the orbit of Saturn.
 According to Kepler's theory, the relative radii of the orbits of the planets can be easily calculated. However, the theory was not born from observations (obviously the discrepancy between the spheres of Jupiter and Mars with the tetrahedron), and Kepler had to drop it
According to Kepler's theory, the relative radii of the orbits of the planets can be easily calculated. However, the theory was not born from observations (obviously the discrepancy between the spheres of Jupiter and Mars with the tetrahedron), and Kepler had to drop itKepler’s idea was indeed ingenious; based on it, it was possible to accurately calculate the ratio of the radii of all orbits. The problem was revealed when comparing calculations with observations. The relations of the calculated radii of the orbits of Mercury and Venus, Venus and Earth, Earth and Mars corresponded to reality quite well, but the last two worlds could not meet the radii predicted by Kepler. In particular, the model was refuted by the orbit of Mars, which did not correspond to any circle. And although Kepler continued to work on it, and even published a second edition 20 years later, his most remarkable contribution was that most scientists are incapable of: discarding their favorite hypothesis.
 The orbits of the planets of the inner solar system are not entirely circular, but they are close to this, and Mercury and Mars deviate most of all from the circle. In addition, comets and asteroids move in ellipses, obeying the rest of Kepler's laws, if only they are gravitationally related to the Sun.
The orbits of the planets of the inner solar system are not entirely circular, but they are close to this, and Mercury and Mars deviate most of all from the circle. In addition, comets and asteroids move in ellipses, obeying the rest of Kepler's laws, if only they are gravitationally related to the Sun.But it was not the nested spheres that managed to predict the movement of the planets, but ellipses.
The three Kepler laws , on the movement of planets in ellipses around the Sun, on equal areas described by radii for equal periods of time, and on equality of relations between the squares of the orbits of planets and the cubes of the major semiaxes of their orbits, have refuted and replaced Mysterium Cosmographicum. The success of elliptical orbits paved the way for Newton's law of the world, and gave rise to astrophysics. Despite Kepler’s unfading love of the most ingenious idea, the Universe was better described by a less elegant model. Having set aside his hopes and letting the experimental data behave further, he was able to achieve breakthroughs that the less gifted mind would not have noticed.
 Kepler's three laws apply to any gravitational system as well as to the solar system.
Kepler's three laws apply to any gravitational system as well as to the solar system.In physics, there is a temptation to succumb to reductionism: to describe as many phenomena as possible with the least possible means. The idea of the existence of the theory of everything, the only theory capable of predicting and describing everything that can be described or predicted in the Universe with the greatest possible accuracy, serves as a dream and the ultimate goal of many scientists. However, there are no guarantees that such a dream can even come true in principle. As the famous physicist Lincoln Wolfenstein wrote:
Kepler’s lesson is not that we should refrain from posing seemingly fundamental questions; the lesson is that we are not given to find out if there are simple answers to them, and where they can be found.
Elegance, beauty and reductionism can open up incredible opportunities for successful predictions of new physical phenomena, but there are no guarantees that these predictions will come true. Making a new breakthrough in fundamental science, our dreams and hopes of approaching the unifying theory of everything with the help of mathematical beauty and additional symmetry are shared by many, but no one guarantees them. May we all be just as open to the fact that we are being informed of the data that Kepler was, and will be able to follow them no matter where they lead us.