
In 1985, the Institute of Electrical and Electronics Engineers (
IEEE ) established the
IEEE 754 standard, which is responsible for
floating point and arithmetic formats, which will become the model for all hardware and software for the next 30 years.
And although most programmers use a floating point at any time indiscriminately, when they need to perform mathematical operations with real numbers, due to certain restrictions on the representation of these numbers, the speed and accuracy of such operations often leave much to be desired.
For many years, the standard was sharply criticized by computer scientists who were familiar with these problems, but
John Gustafson was the most prominent among them, who led a crusade alone to replace the floating point with something more suitable. In this case, posit or
unum is considered a more suitable option - the third option is the result of his study of "universal numbers". He says posit numbers will solve most of the major problems of the IEEE 754 standard, give improved performance and accuracy, and use fewer bits. What's even better, he states that the new format can replace standard floating-point numbers “on the fly,” without having to change the source code of applications.
We met with Gustafson at the ISC19 conference. And for those supercomputer specialists located there, one of the main advantages of the posit format is that you can achieve greater accuracy and dynamic range by using fewer bits than numbers from IEEE 754. And not just a little less. Gustafson said that 32-bit posit replaces 64-bit float in almost all cases, which could have serious consequences for scientific computing. If you halve the number of bits, you can not only reduce the amount of cache, memory and storage for these numbers, but also seriously reduce the width of the channel needed to transfer them to the processor and vice versa. This is the main reason why posit-based arithmetic, in his opinion, will give from double to quadruple calculations in comparison with IEEE floating point numbers.
Acceleration can be achieved through a compact representation of real numbers. Instead of the exponent and the fractional part of a fixed size used in the IEEE standard, posit encodes the exponent with a variable number of bits (a combination of mode bits and exponent bits), so that in most cases they are required less. As a result, more bits remain on the fractional part, which gives greater accuracy. A dynamic exponent is worth using due to its tapering accuracy. This means that quantities with a small exponent, which are most often used, can have greater accuracy, and less commonly used very large and very small numbers will have less accuracy.
Gustafson 's 2017
work describing the posit format gives a detailed description of how this works.
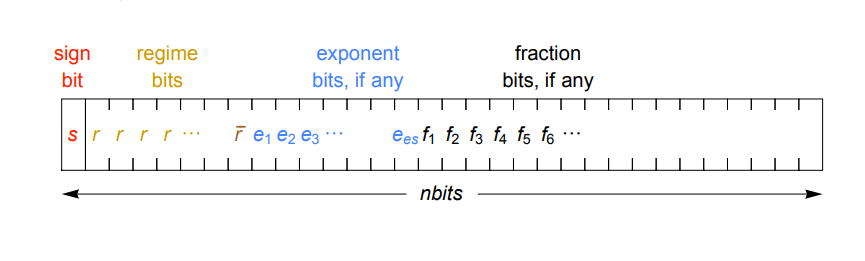
Another important advantage of the format is that, unlike ordinary floating-point numbers, posit give the same bitwise results on any system, which often cannot be guaranteed with the format from IEEE (here even the same calculations on the same system can give different results). Also, the new format deals with rounding errors, overflow and disappearance of significant digits, denormalized numbers, and many values of the type not-a-number (NaN). In addition, posit avoids such oddities as the mismatching values 0 and -0. Instead, the format uses a binary complement for the character, like integers, which means that the bitwise comparison will work correctly.
Something called quire is associated with posit numbers — an accumulation mechanism that allows programmers to perform reproducible linear algebra — a process not available to regular IEEE format numbers. It supports the generalized operation of combined multiplication-addition and other combined operations that allow you to calculate scalar products or sums without rounding errors or overflows. Tests launched at the University of California at Berkeley showed that quire operations are 3-6 times faster than sequential execution. Gustafson says they allow posit numbers to "fight outside their weight class."
Although this number format has only existed for a couple of years, the high-performance computing (HPC) community already has an interest in exploring their applications. At the moment, all the work remains experimental, and is based on the expected speed of the future hardware or on the use of tools that emulate posit arithmetic on conventional processors. While in production there are no chips that implement posit at the hardware level.
One of the potential applications of the format is the
Square Kilometer Array (SKA) radio interferometer under construction, when designing it they
consider posit numbers as a way to radically reduce the channel width and the computational load for processing data coming from the radio telescope. It is necessary that the supercomputers serving it consume no more than 10 MW, and one of the most promising ways to achieve this, according to the designers, is to use a denser posit format in order to halve the estimated width of the memory channel (200 PB / s), the transmission channel data (10 TB / s) and network connection (1 TB / s). Computing power should also increase.
Another application is the use in weather and climate predictions. The British team
showed that 16-bit posit numbers are clearly ahead of the standard 16-bit floating point numbers, and they "have great potential for use in more complex models." The 16-bit posit emulation in this model worked just as well as 64-bit floating point numbers.
Livermore National Laboratory
evaluates posit and other number formats, exploring ways to reduce the amount of data being moved in exaflops supercomputers of the future. In some cases, they also got better results. For example, posit numbers were able to provide superior accuracy in physical calculations such as shock hydrodynamics, and generally outperformed floating point numbers in various dimensions.

Perhaps posit will have the greatest capabilities in the field of machine learning, where 16-bit numbers can be used for learning, and 8-bit numbers for testing. Gustafson said 32-bit floating-point numbers are overkill for training, and in some cases they don’t even show such good results as 16-bit posit, explaining that the IEEE 754 standard “was absolutely not intended for use with AI” .
It is not surprising that the AI community paid attention to them. Facebook Jeff Johnson has developed an experimental platform with FGPA using posit, which demonstrates better energy efficiency compared to both float16 and IEEE's bfloat16 for machine learning tasks. They plan to explore the use of 16-bit quire hardware for training and compare them with competing formats.
It is worth noting that Facebook is
working with Intel on the Nervana Neural Network (NNP) processor, which should accelerate some of the tasks of the social giant related to AI. The option of using the posit format is not ruled out, although it is more likely that Intel will leave its original FlexPoint format for Nervana. In any case, this point is worth tracking.
Gustafson knows at least one AI chip in which they try to use posit numbers in the design, although he does not have the right to divulge the name of the company. The French company Kalray, working with the European Processor Initiative (EPI), has also shown interest in supporting posit in their next-generation Massively Parallel Processor Array (MPPA) accelerator, so this technology can go to
European exaflops supercomputers .
To Gustafson, all this naturally inspires, and he believes that this third attempt to advance his universal numbers may succeed. Unlike versions one and two, posit is easy to implement in hardware. And given the fierce competition in the field of AI, perhaps we should expect the commercial success of the new format. Among other platforms on which posit can expect a bright future are digital signal processing, GPU (for graphics and other computing), devices for the Internet of things, edge computing. And, of course, HPC.
If the technology gets commercial distribution, Gustafson is unlikely to be able to capitalize on its success. His project, as indicated in the 10-page standard, is completely open, and is available for use by any company that wants to develop appropriate software and hardware. Which probably explains the attention to technology from companies such as IBM, Google, Intel, Micron, Rex Computing, Qualcomm, Fujitsu, Huawei and many others.
However, replacing the IEEE 754 with something more suitable is a huge project, even for a person with such an impressive resume as Gustafson’s. Even before working for ClearSpeed, Intel and AMD, he studied ways to improve scientific calculations on modern processors. “I’ve been trying to figure this issue out for the past 30 years,” he said.