
Hello, habrozhiteli! “Predictive modeling in practice” covers all aspects of forecasting, starting with the key stages of data preprocessing, data splitting and the basic principles of model tuning. All stages of modeling are considered on practical examples from real life, in each chapter a detailed code in R is given.
This book can be used as an introduction to predictive models and a guide to their application. Readers who do not have mathematical training will appreciate the intuitive explanations of specific methods, and the attention paid to solving actual problems with real data will help specialists who want to improve their skills.
The authors tried to avoid complex formulas, for mastering the basic material, an understanding of the basic statistical concepts, such as correlation and linear regression analysis, is enough, but mathematical studies are needed to study advanced topics.
Excerpt. 7.5. Calculations
This section will use functions from the R caret, earth, kernlab, and nnet packages.
R has many packages and functions for creating neural networks. These include nnet, neural, and RSNNS packages. The main focus is on the nnet package, which supports basic models of neural networks with one level of hidden variables, weight reduction, and is characterized by a relatively simple syntax. RSNNS supports a wide range of neural networks. Note that Bergmeir and Benitez (2012) have a brief description of the various neural network packages in R. It also provides a tutorial on RSNNS.
Neural networks
For April approximation of the regression model, the nnet function can receive both the formula of the model and the matrix interface. For regression, a linear relationship between hidden variables and forecast is used with the linout = TRUE parameter. The simplest call to the neural network function will look like:
> nnetFit <- nnet(predictors, outcome, + size = 5, + decay = 0.01, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
This call creates one model with five hidden variables. It is assumed that the data in the predictors were standardized on a single scale.
To average the models, the avNNet function from the caret package is used, which has the same syntax:
> nnetAvg <- avNNet(predictors, outcome, + size = 5, + decay = 0.01, + ## + repeats = 5, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
New data points are processed by the command
> predict(nnetFit, newData) > ## > predict(nnetAvg, newData)
To reproduce the previously presented method of choosing the number of hidden variables and the amount of weight reduction through repeated sampling, we apply the train function with the method = “nnet” or method = “avNNet” parameter, first removing the predictors (so that the maximum absolute pair correlation between the predictors does not exceed 0.75):
> ## findCorrelation > ## , > ## > tooHigh <- findCorrelation(cor(solTrainXtrans), cutoff = .75) > trainXnnet <- solTrainXtrans[, -tooHigh] > testXnnet <- solTestXtrans[, -tooHigh] > ## - : > nnetGrid <- expand.grid(.decay = c(0, 0.01, .1), + .size = c(1:10), + ## — + ## (. ) + ## . + .bag = FALSE) > set.seed(100) > nnetTune <- train(solTrainXtrans, solTrainY, + method = "avNNet", + tuneGrid = nnetGrid, + trControl = ctrl, + ## + ## + preProc = c("center", "scale"), + linout = TRUE, + trace = FALSE, + MaxNWts = 10 * (ncol(trainXnnet) + 1) + 10 + 1, + maxit = 500)
Multidimensional adaptive regression splines
MARS models are contained in several packages, but the most extensive implementation is in the earth package. A MARS model using the nominal phase of direct pass and truncation can be called up as follows:
> marsFit <- earth(solTrainXtrans, solTrainY) > marsFit Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Since this model in the internal implementation uses the GCV method to select a model, its structure is somewhat different from the model described earlier in this chapter. The summary method generates more extensive output:
> summary(marsFit) Call: earth(x=solTrainXtrans, y=solTrainY) coefficients (Intercept) -3.223749 FP002 0.517848 FP003 -0.228759 FP059 -0.582140 FP065 -0.273844 FP075 0.285520 FP083 -0.629746 FP085 -0.235622 FP099 0.325018 FP111 -0.403920 FP135 0.394901 FP142 0.407264 FP154 -0.620757 FP172 -0.514016 FP176 0.308482 FP188 0.425123 FP202 0.302688 FP204 -0.311739 FP207 0.457080 h(MolWeight-5.77508) -1.801853 h(5.94516-MolWeight) 0.813322 h(NumNonHAtoms-2.99573) -3.247622 h(2.99573-NumNonHAtoms) 2.520305 h(2.57858-NumNonHBonds) -0.564690 h(NumMultBonds-1.85275) -0.370480 h(NumRotBonds-2.19722) -2.753687 h(2.19722-NumRotBonds) 0.123978 h(NumAromaticBonds-2.48491) -1.453716 h(NumNitrogen-0.584815) 8.239716 h(0.584815-NumNitrogen) -1.542868 h(NumOxygen-1.38629) 3.304643 h(1.38629-NumOxygen) -0.620413 h(NumChlorine-0.46875) -50.431489 h(HydrophilicFactor- -0.816625) 0.237565 h(-0.816625-HydrophilicFactor) -0.370998 h(SurfaceArea1-1.9554) 0.149166 h(SurfaceArea2-4.66178) -0.169960 h(4.66178-SurfaceArea2) -0.157970 Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
In this derivation, h (·) is the hinge function. In the presented results, the component h (MolWeight-5.77508) is equal to zero for a molecular weight of less than 5.77508 (as in the upper part of Fig. 7.3). The reflected hinge function has the form h (5.77508 - MolWeight).
The plotmo function from the earth package can be used to build diagrams similar to those shown in fig. 7.5. You can use train to configure the model using external re-fetching. The following code reproduces the results shown in fig. 7.4:
> # - > marsGrid <- expand.grid(.degree = 1:2, .nprune = 2:38) > # > set.seed(100) > marsTuned <- train(solTrainXtrans, solTrainY, + method = "earth", + # - + tuneGrid = marsGrid, + trControl = trainControl(method = "cv")) > marsTuned 951 samples 228 predictors No pre-processing Resampling: Cross-Validation (10-fold) Summary of sample sizes: 856, 857, 855, 856, 856, 855, ... Resampling results across tuning parameters: degree nprune RMSE Rsquared RMSE SD Rsquared SD 1 2 1.54 0.438 0.128 0.0802 1 3 1.12 0.7 0.0968 0.0647 1 4 1.06 0.73 0.0849 0.0594 1 5 1.02 0.75 0.102 0.0551 1 6 0.984 0.768 0.0733 0.042 1 7 0.919 0.796 0.0657 0.0432 1 8 0.862 0.821 0.0418 0.0237 : : : : : : 2 33 0.701 0.883 0.068 0.0307 2 34 0.702 0.883 0.0699 0.0307 2 35 0.696 0.885 0.0746 0.0315 2 36 0.687 0.887 0.0604 0.0281 2 37 0.696 0.885 0.0689 0.0291 2 38 0.686 0.887 0.0626 0.029 RMSE was used to select the optimal model using the smallest value. The final values used for the model were degree = 1 and nprune = 38. > head(predict(marsTuned, solTestXtrans)) [1] 0.3677522 -0.1503220 -0.5051844 0.5398116 -0.4792718 0.7377222
Two functions are used to evaluate the importance of each predictor in the MARS model: evimp from the earth package and varImp from the caret package (the second calls the first):
> varImp(marsTuned) earth variable importance only 20 most important variables shown (out of 228) Overall MolWeight 100.00 NumNonHAtoms 89.96 SurfaceArea2 89.51 SurfaceArea1 57.34 FP142 44.31 FP002 39.23 NumMultBond s 39.23 FP204 37.10 FP172 34.96 NumOxygen 30.70 NumNitrogen 29.12 FP083 28.21 NumNonHBonds 26.58 FP059 24.76 FP135 23.51 FP154 21.20 FP207 19.05 FP202 17.92 NumRotBonds 16.94 FP085 16.02
These results are scaled in the range from 0 to 100, differing from those given in table. 7.1 (the model presented in Table 7.1 did not go through the complete process of growth and truncation). Note that the variables following the first few of them are less significant for the model.
SVM, support vector method
Implementations of SVM models are contained in several R. packages. Chang and Lin (Chang and Lin, 2011) use the svm function from the e1071 package to use the interface to the LIBSVM library for regression. A more complete implementation of SVM models for Karatsogl regression (Karatzoglou et al., 2004) is contained in the kernlab package, which includes the ksvm function for regression models and a large number of nuclear functions. By default, the radial basis function is used. If the values of cost and nuclear parameters are known, then the approximation of the model can be performed as follows:
> svmFit <- ksvm(x = solTrainXtrans, y = solTrainY, + kernel ="rbfdot", kpar = "automatic", + C = 1, epsilon = 0.1)
To estimate σ, automated analysis was used. Since y is a numerical vector, the function obviously approximates the regression model (instead of the classification model). You can use other kernel functions, including polynomial (kernel = "polydot") and linear (kernel = "vanilladot").
If the values are unknown, then they can be estimated by re-sampling. In train, the values of "svmRadial", "svmLinear" or "svmPoly" of the method parameter select different kernel functions:
> svmRTuned <- train(solTrainXtrans, solTrainY, + method = "svmRadial", + preProc = c("center", "scale"), + tuneLength = 14, + trControl = trainControl(method = "cv"))
The tuneLength argument uses 14 default values.

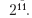
A default estimate of σ is performed through automatic analysis.
> svmRTuned 951 samples 228 predictors Pre-processing: centered, scaled Resampling: Cross-Validation (10-fold) Summary of sample sizes: 855, 858, 856, 855, 855, 856, ... Resampling results across tuning parameters: C RMSE Rsquared RMSE SD Rsquared SD 0.25 0.793 0.87 0.105 0.0396 0.5 0.708 0.889 0.0936 0.0345 1 0.664 0.898 0.0834 0.0306 2 0.642 0.903 0.0725 0.0277 4 0.629 0.906 0.067 0.0253 8 0.621 0.908 0.0634 0.0238 16 0.617 0.909 0.0602 0.0232 32 0.613 0.91 0.06 0.0234 64 0.611 0.911 0.0586 0.0231 128 0.609 0.911 0.0561 0.0223 256 0.609 0.911 0.056 0.0224 512 0.61 0.911 0.0563 0.0226 1020 0.613 0.91 0.0563 0.023 2050 0.618 0.909 0.0541 0.023 Tuning parameter 'sigma' was held constant at a value of 0.00387 RMSE was used to select the optimal model using the smallest value. The final values used for the model were C = 256 and sigma = 0.00387.
The finalModel subobject contains the model created by the ksvm function:
> svmRTuned$finalModel Support Vector Machine object of class "ksvm" SV type: eps-svr (regression) parameter : epsilon = 0.1 cost C = 256 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 0.00387037424967707 Number of Support Vectors : 625 Objective Function Value : -1020.558 Training error : 0.009163
As reference vectors, the model uses 625 data points of the training set (i.e. 66% of the training set).
The kernlab package contains an implementation of the RVM model for regression in the rvm function. Its syntax is very similar to that presented in the example for ksvm.
KNN Method
The caren package knnreg approximates the KNN regression model; train function sets the model to K:
> # . > knnDescr <- solTrainXtrans[, -nearZeroVar(solTrainXtrans)] > set.seed(100) > knnTune <- train(knnDescr, + solTrainY, + method = "knn", + # + # + preProc = c("center", "scale"), + tuneGrid = data.frame(.k = 1:20), + trControl = trainControl(method = "cv"))
About the authors:
Max Kun is Head of Pfizer Global's Non-Clinical Research and Development Division. He has been working with predictive models for over 15 years and is the author of several specialized packages for the R language. Predictive modeling in practice covers all aspects of forecasting, starting with the key stages of data preprocessing, data splitting, and basic principles
model settings. All stages of modeling are considered on practical examples.
from real life, each chapter gives a detailed code in R.
Kjell Johnson has been working in the field of statistics and predictive modeling for pharmaceutical research for more than ten years. Co-founder of Arbor Analytics, a company specializing in predictive modeling; previously headed the department of statistical research and development at Pfizer Global. His scientific work is devoted to the application and development of statistical methodology and learning algorithms.
»More details on the book can be found on
the publisher’s website»
Contents»
Excerpt25% off coupon for hawkers -
Applied Predictive ModelingUpon payment of the paper version of the book, an electronic book is sent by e-mail.