Content
Part 2 - Semi-solution of the two-body problemHello to all! Today I will begin a series of lecture articles on the topic of designing unmanned aerial vehicles for space purposes (rockets) =). Yes, yes - you heard right about the real missiles, we’ll learn to design them in real fashion, as (probably) they do in some
design bureau . I myself graduated from the university precisely in this specialty, because some knowledge is available. But he himself has not worked a day in KB (unfortunately). Due to the corresponding arrangement of stars in the sky. In general, the stars agreed so, I have such a fate. Although he could have worked in the Yuzhny Design Bureau for half a year already, he was almost settled in winter, all that remained was to go through the medical board and submit the documents for verification to the
SBU in order to obtain a security clearance. But again something went wrong. This has already happened a lot of times, because something must have accumulated has fired, and I decided:
on the hell .
And by the way, a month ago I sent a resume to SpaceX to a mechanical engineer, but two days later they politely refused me, because the law is
ITAR . Well, the attempt is not torture, but I really just wanted to go help something, and I’m not a special agent. Well, okay, I’ll probably start on the topic, otherwise I spread the story of my life here (I just had to fill in the beginning with something, I thought, I thought - I wrote it as it is).
Introduction
Although my specialty is more focused on designing air-to-air, air-to-ground, and ground-to-air missiles that fly not so far (several tens of kilometers) and not so long (less than a minute), and “useful load ”they have not so useful. Especially when civilian planes are shot down by mistake and people die innocent. Okay, destroy each other’s equipment, it’s such a thing - it’s nice to look at explosions and destruction. But violating the laws of God “love your neighbor as yourself” is wrong.
So, although my specialization is not for the cosmic scale, but I think we can handle it. Especially for six months or a year, in their fifth year they passed by "the design of spacecraft intended for space exploration." And in fact, only orbital mechanics was new to us there. And in terms of missile design, it’s even easier there, because they don’t need to experience such frenzied overloads of 10-20 units in the longitudinal and transverse directions at the same time. And aerodynamics are almost unimportant there. Management is only a deviation of the engines. Well, the engines there, however, are more complicated -
LRE . It's okay, we will try to design a space rocket entirely on
solid propellant rocket engines . Solid propellant rocket motors are simple to design, even if solid fuels have an energy intensity two times lower - it’s okay. Maybe it will work out, maybe not, it must be considered, so you won’t say it right away. We'll figure it out along the way. Like that, let's go.
Orbital mechanics
We are flying into space. How to fly, where to fly, when,
why . Orbital mechanics will give us answers to these questions. Therefore, the first thing to deal with this contraption. Fortunately, it is simple (at least at first glance). Just something - 1, 2, 3 laws of Newton and the law of gravity of Sir Isaac. Stars and planets are considered as material points, which is justified by the gigantic distances between them in comparison with their very sizes.
For example, here is a picture on a scale: of the Sun and the planet Mercury closest to it:
 The relative sizes of the Sun, Mercury and the distances between them are strictly observed. (The black pixel is Mercury, the blue line is the trajectory of its movement)
The relative sizes of the Sun, Mercury and the distances between them are strictly observed. (The black pixel is Mercury, the blue line is the trajectory of its movement)But on a scale the whole solar system:
 And here already the Sun looks like a point, planets and even more so.
And here already the Sun looks like a point, planets and even more so.And for complete happiness, a beautiful picture and Vicki with the relative sizes of celestial bodies:
 Planets of the Solar System
Planets of the Solar SystemRecall Newton’s laws. The second says that power
applied to the body by mass
causes acceleration
of this body in the direction of force, and moreover, it is equal to the product of mass and acceleration:
The first law states that if forces are not acting on the body
, then the body moves at a constant speed. Or doesn’t move at all = moves at a constant speed equal to zero:
And the Third Law explains how two bodies interact: the first body acts on the second with the same force as the second on the first:
forces are equal in magnitude, but directed opposite.
The law of gravity looks like this:
here
- gravitational constant
- masses of the first and second body,
- distance between bodies.
And the force is directed from the body on which it acts to the body of a
girl with a square , with which there is an interaction.
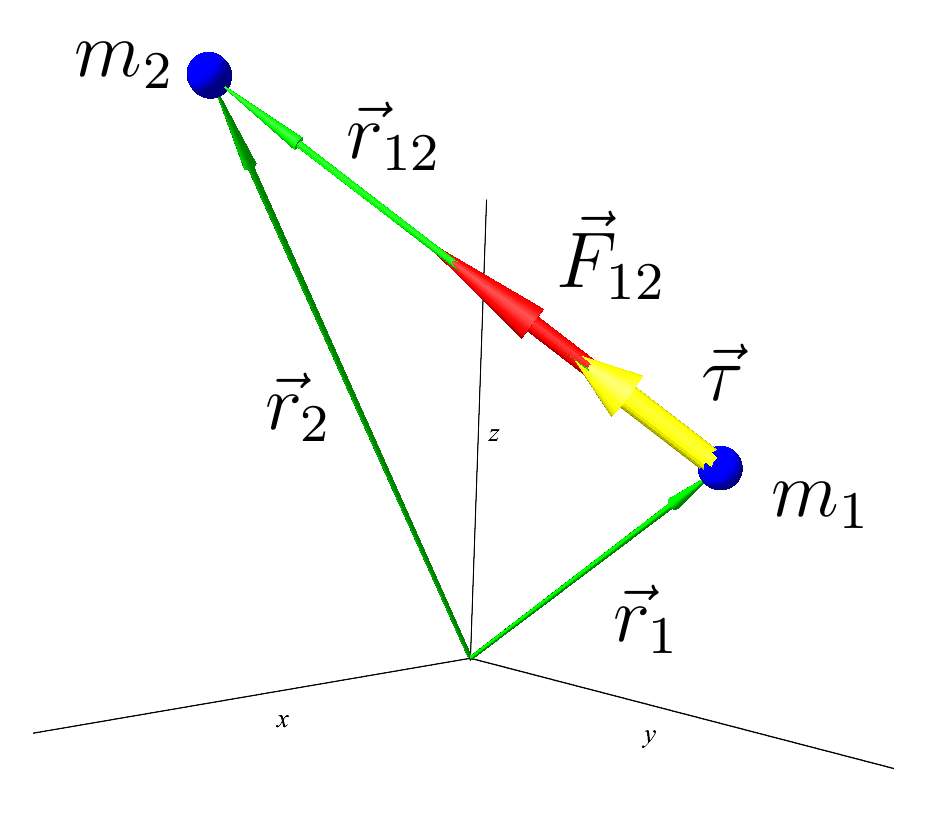 Gravity
GravityNow for two interacting material points, you can write, based on the above recorded laws. For the first body:
here
Is a unit vector directed from the first body towards the second. BUT
- from the picture you can see. AND
- the distance between the bodies.
We rewrite 1:
For the second body, everything will be similar, but plus according to Newton’s third law (
):
Total for a system of two material points, we have a system of differential equations written in vector form:
\ begin {equation *}
\ begin {cases}
m_ {1} \ ddot {\ vec {r}} _ {1} = \ vec {F} _ {12},
\\
m_ {2} \ ddot {\ vec {r}} _ {2} = - \ vec {F} _ {12}
\ end {cases}
\ end {equation *}
What can I say, it turns out beautifully for a two-body system, I even want to immediately add these equalities or subtract them.
For a system of many N material points, everything will be the same, but the interaction will have to be taken into account in pairs. Instead of two vector equalities, there will be N pieces. And everyone on the right will have a sum of strength. If we go further and consider the “continuum” of points, that is, a solid body - the total force will be obtained by integration over the area occupied by the body. Everything is as usual: an infinite small part of the body dV is considered and summed-integrated. This procedure is simplified by using the so-called “potential” of force, because our strength is potential, has potential, but we will talk about this in the future, and perhaps we will get a field around a spherical body. Because spherical bodies are a common thing in space. The fact that they are almost spherical, and how this is taken into account, will also be discussed in the future.
Now back to the two-body system. Firstly, it is notable for the fact that this is the first task in complexity after a system of one body. And mathematically investigating this problem is primarily due to this fact. And on the other hand, as it turns out,
this model can be described
space motion =) (but this is inaccurate).
Well, for example, planets move around the Sun very much almost independently of each other. Now let's evaluate this for the Earth-Mars-Sun system. It’s good that we live in a time when it’s enough to send the correct request to the Internet, and you will receive all the necessary information:
earth mass
kg
mass of the sun relative to the earth
Mars mass relative to the Earth
Earth's distance from the Sun
distance of Mars from the Sun
Now it’s easy to calculate the forces acting on the Earth from the side of the central luminary and a piece of spherical material named after the ancient Roman god of war (sorry for poetry, something came upon me):
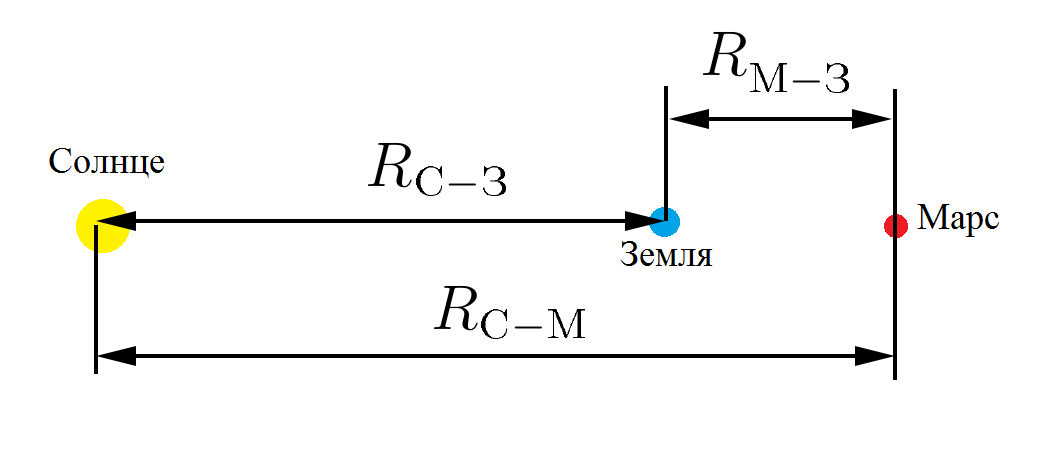 Sun, Earth and Mars
Sun, Earth and Marsor rather, we do not even need the values of these forces, only their relationship:
Wow. Almost a million times stronger, the Sun attracts the Earth than Mars in its best years. I mean when Mars-Earth-Sun are located on one straight line. With a different location, Mars will attract even worse. Well, I don’t even know what analogy to bring, maybe it’s like the ratio of the weight forces of one coin against a tyrannosaurus.
So it is with the rest of the celestial host of the solar system: the sun affects every individual, while they almost do not affect each other. I did not check in pairs, but I think so. Perhaps this is a consequence, including the fact that the mass of the solar system is equal to:
that is, the whole mass is concentrated in the sun, and
solar mass - planets, comets, gas and all kinds of rubbish.
The second example where a two-body model will help us is the movement of an artificial satellite near the Earth. Here, similarly, the Earth has a colossal mass in comparison with the satellite. And even one more illustrative example of the calculations of the Earth-satellite-Moon system can be given. The following forces act on the satellite:
it’s just that the mass of the earth is 81 times the mass of the moon. And we took the distance here in half, that is, the middle between the Earth and the Moon. And finally, the ratio of these forces:
Conclusion: even when the satellite flies exactly between the Earth and the Moon, and this is an orbit of 192,200 km, the Earth will still attract our artificial satellite 81 times stronger than the Moon. For comparison, we will depict this by two vectors of forces located nearby, the lengths of which will differ 100 times. Here, we simply rounded off the engineering, because for an engineer - 80 is the same as 100. This is like a well-known engineering equality, who do not know:
 Comparison of the forces of action on a satellite from the side of the Earth and the Moon
Comparison of the forces of action on a satellite from the side of the Earth and the MoonIn the next article, we solve analytically the two-body problem.
Continuation