In the first
publication, it was said that there is an forgotten Erds-Renyi theorem, from which it follows that in a random series of length N, with a probability close to 1, there exists a row of identical values of length
. The indicated property of a random variable can be used to answer the question: “After processing big data, is the residual series obeying the law of random numbers or not?”
The answer to this question was determined not on the basis of tests of correspondence to the normality of distribution, but on the basis of the properties of the residual series itself.
By the presence or absence or shift of the frequency of the contracts of the same characters. I tried in the publication to show the possibilities of using this tool, although many questions arose about how this works in reality when conducting analysis in big data. But the discussion was productive, and the
VDG user even presented a real example:
“... The dendritic branches of a neuron can be represented as a bit sequence. A branch, and then the entire neuron, is triggered when a chain of synapses is activated in any of its places. The neuron has the task of not responding to white noise, respectively, the minimum length of the chain, as far as I remember at Numenta, is 14 synapses for the pyramidal neuron with its 10 thousand synapses. And according to the formula we get: . That is, chains less than 14 in length will occur due to natural noise, but will not activate the neuron. It’s perfectly laid right .
”Let's try to consider the mechanism presented in this material.
The first publication raised many questions. Let us try to clarify the mechanism of the Erds-Renyi theorem in this article.
The solution came about in connection with the
Penny Game paradox. The game consists in the following - two players A and B are going to throw a coin five times, assigning, for example, “eagle” - 1, “tails” - 0. Player A chooses a sequence of three values and voices it, suppose 001.
Player B chooses his sequence, suppose 100. The player whose sequence falls first is the winner. Suppose that 01001 has fallen, that is, 0-100-1, which corresponds to the choice of B. The paradox of the “Penny Game” is that no matter which sequence A player chooses, player B always has the opportunity to choose a sequence whose probability of occurrence is greater than the sequence chosen by player A. The winning matrix of player B is shown in Figure 1.
 Fig. 1. The payoff matrix of player B in the “Penny Game” for five shots.
Fig. 1. The payoff matrix of player B in the “Penny Game” for five shots.The effect of this paradox is that the random series is not transitive, that is, if U> R, and R> Q, then this does not mean that Q> U.
The consequence of this paradox is the following ordinary things, if a player plays by the rules and complies with the laws of probability theory:
- He usually wins in gambling, the one whose cashier is bigger is “crush the bank”.
- In a casino, only the casino wins.
- When playing on the stock exchange, only luck determines how long a trader will last until he loses his capital.
The physical meaning of this law, on which the “Penny Game” paradox is based, is that the advantage is given to the one who can continue the random sequence more. As in the first example - a player who has more cash. In the second option - the casino plays with hundreds of sequences at the same time, and will continue to play after any of the players stops the game. A game against a single player’s exchange does not compare with millions of operations on the exchange.
As you can see, the first law was drawn - BigData determines the situation in comparison with local information.
The second defining moment is the absence of the transitivity property of random sequences. The consequence of this is the inability to roll back the situation.
Further hypothesis in the analysis of BigData:
1) Understanding of developing events is possible only on such a volume in which the consequences of the events under investigation are recorded. The mechanism for this process can be represented as follows. A random field is a field in which several potential processes try to realize themselves. After self-realization, the process leaves changes, and we try to detect the degree of traces from the processes that have occurred. Dependencies are already determined by the proportion of the left results. I will explain to the above that, in my opinion, the way the transformations themselves occur, at the moment, science cannot give a formal definition. If these definitions were, then some of Zeno’s paradoxes would cease to be paradoxes, and the unity and struggle of opposites, materialistic dialectics would cease to be a postulate in it.
I suppose that it is not worth breaking the spears of statements that if we determine the process after the fact, then this is a meaningless exercise, since the next process will be unpredictable. A person sees quite locally, and BigData processes can last billions of years, so we have the opportunity to see the mechanism of a process from the BigData field. Interesting material on the great values of the universe is presented
here .
2) The second hypothesis, which can be deduced from the absence of the transitivity property, is the influence of the interval and conditions on the process under study. That is, on the one hand, there is a time coordinate that positions the process under study, and a chance to repeat the conditions under which our process was formed, and millions of records were received, is almost impossible. On the other hand, the laws of combinatorics cannot be ignored. These laws tell us that the probability of a certain combination occurring must always exist. Figure 2 shows the distribution of variants of chains of N signals in which there are rows of sub-orders of length k. The total amount is greater than
, since short chains are combined with longer ones.
 Fig. 2. The number of possible sub-order variants of k identical signals, in a sequence of N values.
Fig. 2. The number of possible sub-order variants of k identical signals, in a sequence of N values.For variants in which chains longer than N / 2 are present, they are filled in yellow, their number is determined in a fairly simple way by the formula:

That is, the corresponding probabilities for series containing chains of k> = N / 2 identical values (we will not describe the probability of a series of N values) will be determined by the formula:
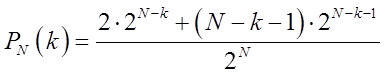
During the discussion, in the first part, questions arose, the essence of which was as follows: “Where are the boundaries of white noise?” Here, considering the table of Figure 2, a hypothesis was formed for discussion, according to the following scheme.
Based on the Muavre-Laplace integral theorem:

We define the intervals for f (1.96) = 95% probability:

If you look, the table in Figure 2 reflects the full probability field, on the other hand, the distribution parameters in each case are uniquely definable, and are presented in Figure 3, where we show them using an example of a series of 9 values. Since the number of options
, and for this number of tests we will find alpha.
 Fig. 3. The boundaries of the probability intervals of sub-orders of length k of the same signals, in a sequence of 9 values, with a reliability of 2 sigma (95%).
Fig. 3. The boundaries of the probability intervals of sub-orders of length k of the same signals, in a sequence of 9 values, with a reliability of 2 sigma (95%).Figure 4 presented the intervals for the random variable, where Figure 4b is the transposed Figure 4a.
 Fig. 4. Intervals of random size for each suborder, with a reliability of 95%.
Fig. 4. Intervals of random size for each suborder, with a reliability of 95%.In order to somehow structure the answers to the questions of where the white noise is, he formulated the existing approaches as follows:
- White noise is recognized by the community;
- Data that can be formulated with analytical expressions;
- Information structured by neural networks;
- Qubits, quantum computers;
- BigData
- If big data exists, then it is entirely possible that hyperdata exists.
For the proposed structuring, the clue turned out to be the idea of O. V. Filatov
“Definition of a random binary sequence as a combinatorial object. Calculation of coincident fragments in random binary sequences ” about the behavior of fragments of a sequence resembling the behavior of particles in the microworld.
The qubits, which have a three-dimensional structure, suggest that the structural scheme should have a three-dimensional model. Several layers, which are recognized by the community, implied the layering of the model and, combining all this, the most elegant scheme is possible in the form of a toroid, Figure 5.
 Fig. 5. The assumption of the structure of the data in the mapping of random variables onto the space (pictures taken from the Internet).
Fig. 5. The assumption of the structure of the data in the mapping of random variables onto the space (pictures taken from the Internet).Developing the reasoning further, we note that in Figure 3, all frequencies are even numbers. This is a consequence of the symmetry of the data "0-1". The symmetry of random data is reflected in
Solomon Wolf Golomb 's Postulates of the Golomb . Based on the research Filatova O.V.
“Derivation of formulas for the postulates of Golomb. A way to create a pseudo-random sequence from Mises frequencies. The Basics of “Combinatorics of Long Sequences” uses the concept of a half-wave. I believe that this aspect is significant in the study of white noise, as it is associated with parameters such as row length.
Given the properties of random processes, a white noise wave can acquire various properties, including the lack
of wave
symmetry and possible non-compliance with
Noether's theorem . But there are processes in the physical world like the formation of foam of a surf wave, Figure 6. So we have every reason to allow unusual parameters of white noise waves.
 Fig. 6. The mechanism of wave deformation near the coast and examples of processes that, when projected onto some hyperplanes, in local space, may look like a random process (pictures taken from the Internet).
Fig. 6. The mechanism of wave deformation near the coast and examples of processes that, when projected onto some hyperplanes, in local space, may look like a random process (pictures taken from the Internet).Turning to the practical part, I will summarize the proposed approaches when working with white noise.
- Lack of transitivity property in random processes.
- The assumption that the symmetry properties in white noise are the realization of the symmetry properties of processes higher than the processes in the current situation under consideration.
- Locality of random processes. This premise is not explicitly shown in the publication, but fits well enough in the framework of constructive mathematics. You all use it (constructive mathematics) when you write a script that sets the requirement to access a memory cell and read its contents. Since by default you mean that in this cell there is a certain value 0 or 1 and nothing else can be there. Good material to familiarize yourself with her approaches is presented here: N.N. Nepeyvoda “Constructive mathematics: a review of achievements, weaknesses and lessons. Part I " .
Practical part
In the first part, the question of the Erds-Renyi theorem was examined, which consisted in the fact that this theorem was found only in one source, which is translated from Hungarian, this book was published back in the USSR and no evidence or mention of it was found . As a consequence of this fact, there was an uncertainty in general of its existence and, especially, its application.
As a result of searches, it was discovered in the work of Filatov O.V.
“Derivation of formulas for the postulates of Golomb. A way to create a pseudo-random sequence from Mises frequencies. The basics of “Combinatorics of long sequences” p. 15 the following, Figure 7, I quote the original from the material.
 Fig. 7. The original part of the publication Filatova OV “Derivation of formulas for the postulates of Golomb. A way to create a pseudo-random sequence from Mises frequencies. Fundamentals of "Combinatorics of long sequences."
Fig. 7. The original part of the publication Filatova OV “Derivation of formulas for the postulates of Golomb. A way to create a pseudo-random sequence from Mises frequencies. Fundamentals of "Combinatorics of long sequences."Erds-Renyi theorem is formulated as follows:
When tossing a coin N times, a series of falling equal sides of a coin in a row of length
observed with a probability tending to 1, with N tending to infinity.
We write the theorem in the formulations “Combinatorics of long sequences” for one side of the coin:

We carry out the proof:

As you can see the Mises frequencies for a train consisting of a chain of identical signals of length
coincide with the conclusions of the Erdos-Renyi theorem on the probability of the same chain in the case of a random series. So you can eliminate the doubt and acknowledge its existence and possibility of application.
Since the publication was already more recommended by marketers, the continuation in the next part, “White noise draws a black square. Part 3. Application. "