So, imagine. 5 cats are locked in the room, and in order to go to wake up the owner they need to all agree on this together, because they can open the door only by leaning on five of them. If one of the cats is a Schrodinger cat, and the rest of the cats do not know about its solution, the question arises: “How can they do this?”
In this article, I will tell you in simple language about the theoretical component of the world of distributed systems and the principles of their operation. And also superficially consider the main idea underlying Paxos'a.
When developers use cloud infrastructures, various databases, work in clusters from a large number of nodes, they are sure that the data will be complete, secure and always accessible. But where are the guarantees?
In fact, the guarantees that we have are the guarantees of the supplier. They are described in the documentation in approximately the following way: "This service is quite reliable, it has a predefined SLA, do not worry, everything will work in a distributed manner, as you expect."
We tend to believe in the best, because smart uncles from large companies have assured us that everything will be fine. We do not ask ourselves: why, in fact, can it even work? Is there any formal justification for the correct operation of such systems?
I recently went to
school on distributed computing and was very inspired by this topic. Lectures at the school looked more like classes in mathematical analysis than something related to computer systems. But this is precisely how the most important algorithms that we use every day without knowing it were proved at one time.
Most modern distributed systems use the Paxos consensus algorithm and its various modifications. The coolest thing is that the validity and, in principle, the very possibility of the existence of this algorithm can be proved simply with a pen and paper. However, in practice, the algorithm is used in large systems operating on a huge number of nodes in the clouds.
Light illustration of what will be discussed further: the task of two generalsLet’s take a look
at the two generals task to warm up.
We have two armies - red and white. White troops are based in the besieged city. Red troops led by generals A1 and A2 are located on two sides of the city. The task of the redheads is to attack the white city and win. However, the army of each red-headed general individually is smaller than the troops of the whites.
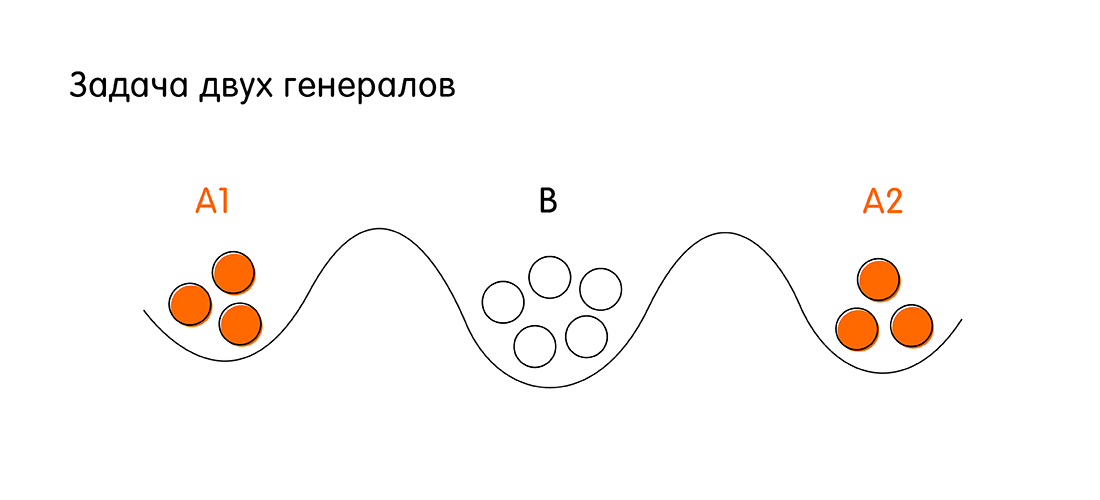
Victory conditions for redheads: both generals must attack simultaneously in order to have a numerical advantage over whites. For this, Generals A1 and A2 need to agree with each other. If everyone attacks individually, the redheads will lose.
To agree, generals A1 and A2 can send messengers to each other through the territory of the white city. A messenger can successfully get to an allied general or can be intercepted by an adversary. Question: is there such a sequence of communications between the red generals (the sequence of sending messengers from A1 to A2 and vice versa from A2 to A1), in which they are guaranteed to agree on an attack at hour H. Here, under the guarantees it is understood that both generals will have unequivocal confirmation that an ally (another general) accurately attacks at the appointed time X.
Suppose A1 sends a messenger to A2 with the message: “Let's attack today at midnight!” General A1 cannot attack without confirmation from General A2. If the messenger has reached A1, then General A2 sends a confirmation with the message: “Yes, let's fill up the whites today.” But now, General A2 does not know whether his messenger has arrived or not, he has no guarantees whether the attack will be simultaneous. Now General A2 needs confirmation again.
If we schedule their communication further, it turns out the following: no matter how many messaging cycles there is, there is no way to guarantee to notify both generals that their messages have been received (provided that any of the messengers can be intercepted).
The task of two generals is a great illustration of a very simple distributed system, where there are two nodes with unreliable communication. So we don’t have a 100% guarantee that they are synchronized. About similar problems only on a larger scale later in the article.
We introduce the concept of distributed systems
A distributed system is a group of computers (hereinafter referred to as nodes) that can exchange messages. Each individual node is an autonomous entity. A node can independently process tasks, but in order to interact with other nodes, it needs to send and receive messages.
How specifically the messages are implemented, which protocols are used - this is not of interest to us in this context. It is important that the nodes of a distributed system can exchange data with each other by sending messages.
The definition itself does not look very complicated, but you need to consider that a distributed system has a number of attributes that will be important to us.
Distributed System Attributes
- Concurrency - the possibility of simultaneous or competitive events in the system. Moreover, we will consider that the events that occurred on two different nodes are potentially competitive as long as we do not have a clear order of occurrence of these events. And, as a rule, we don’t have it.
- The lack of a global clock . We do not have a clear order of events due to the lack of a global clock. In the ordinary world of people, we are used to the fact that we have hours and time absolutely. Everything changes when it comes to distributed systems. Even ultra-precise atomic clocks have a drift, and there may be situations where we cannot say which of the two events happened earlier. Therefore, we also cannot rely on time.
- Independent failure of system nodes . There is another problem: something may not be so simple because our nodes are not eternal. The hard disk may fail, the virtual machine in the cloud will reboot, the network may blink and messages will be lost. Moreover, situations are possible when the nodes work, but at the same time work against the system. The latter class of problems even received a separate name: the problem of Byzantine generals . The most popular example of a distributed system with such a problem is Blockchain. But today we will not consider this particular class of problems. We will be interested in situations in which just one or more nodes can fail.
- Communication models (messaging models) between nodes . We have already found out that nodes communicate through messaging. There are two well-known messaging models: synchronous and asynchronous.
Communication models between nodes in distributed systems
Synchronous model - we know for sure that there is a finite known time delta for which a message is guaranteed to reach from one node to another. If this time has passed, but the message has not arrived, we can safely say that the node has failed. In such a model, we have a predictable wait time.
Asynchronous model - in asynchronous models, we believe that the waiting time is finite, but there is no such delta time after which it can be guaranteed that the node is out of order. Those. the waiting time for a message from the node can be arbitrarily long. This is an important definition, and we will talk about this further.
The concept of consensus in distributed systems
Before formally defining the concept of consensus, let us consider an example of the situation when we need it, namely,
State Machine Replication .
We have some distributed log. We would like it to be consistent and contain identical data on all nodes of a distributed system. When one of the nodes finds out a new value that it is going to write to the log, it becomes his task to offer this value to all other nodes so that the log is updated on all nodes and the system switches to a new consistent state. It is important that the nodes agree among themselves: all nodes agree that the proposed new value is correct, all nodes accept this value, and only in this case everyone can write a new value to the log.
In other words: none of the nodes objected that it has more relevant information, and the proposed value is incorrect. The agreement between the nodes and the agreement on a single correct accepted value is consensus in a distributed system. Further we will talk about algorithms that allow a distributed system to achieve consensus with guarantee.

More formally, we can define a consensus algorithm (or just a consensus algorithm) as a function that transfers a distributed system from state A to state B. Moreover, this state is accepted by all nodes, and all nodes can confirm it. As it turns out, this task is not at all as trivial as it seems at first glance.
Consensus Algorithm Properties
The consensus algorithm must have three properties so that the system continues to exist and has some progress in the transition from state to state:
- Agreement - all correctly working nodes must take the same value (in articles this property is also found as a safety property). All nodes that are currently functioning (not out of order and have not lost touch with the rest) must come to an agreement and take on some kind of final general meaning.
It is important to understand here that the nodes in the distributed system we are considering want to agree. That is, we are now talking about systems that just might fail (for example, to fail a node), but this system definitely does not have nodes that intentionally work against others (the task of the Byzantine generals). Due to this property, the system remains consistent. - Integrity - if all correctly working nodes offer the same value of v , then each correctly working node must accept this value of v .
- Termination - all correctly working nodes will eventually take some value (liveness property), which allows the algorithm to have progress in the system. Each individual node that works correctly must sooner or later accept the final value and confirm this: “For me, this value is true, I agree with the whole system.”
Consensus Algorithm Example
While the properties of the algorithm may not be entirely clear. Therefore, we illustrate with an example what stages the simplest consensus algorithm goes through in a system with a synchronous messaging model, in which all nodes function as expected, messages are not lost and nothing breaks (does this really happen?).
- It all starts with a marriage proposal (Propose). Suppose that a client connected to a node called “Node 1” and started a transaction, passing a new value to the node - O. From now on, “Node 1” we will call proposer . As a proposer, “Node 1” should now notify the whole system that it has fresh data, and it will send messages to all other nodes: “Look! I got the value “O” and I want to write it down! Please confirm that you will also write “O” in your log. ”
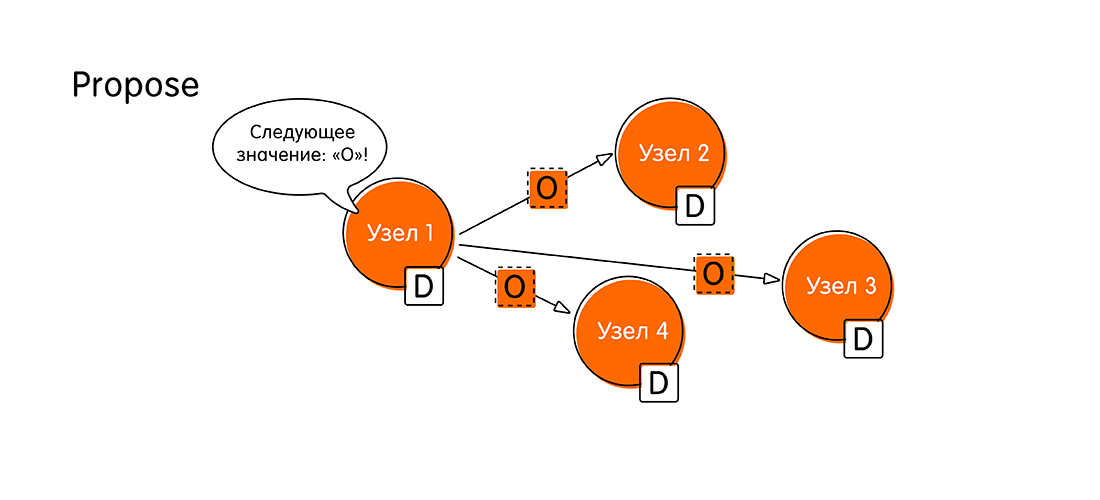
- The next stage is voting for the proposed value (Voting). What is it for? It may happen that other nodes received more recent information, and they have data on the same transaction.
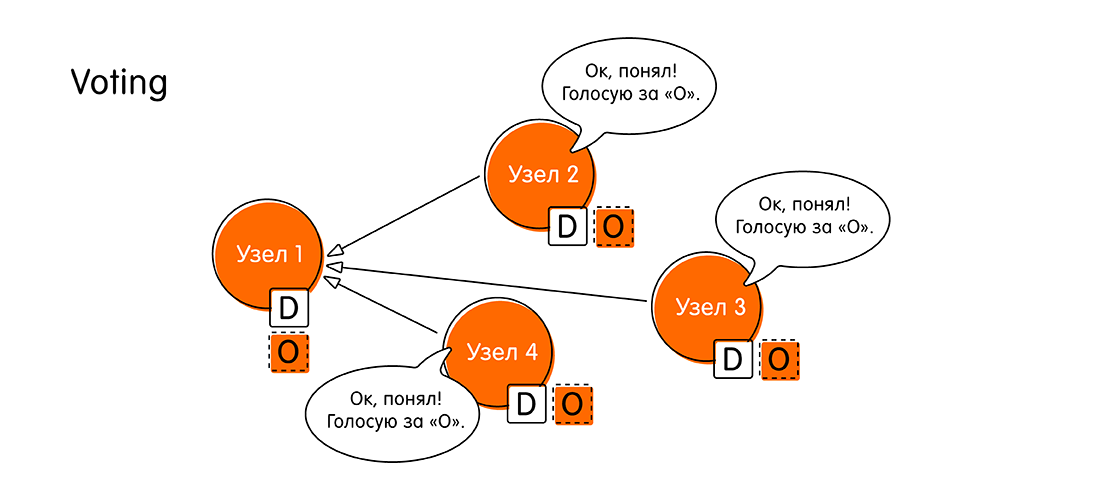
When the node “Node 1” sends its own message, the other nodes check the data for this event in their logs. If there are no contradictions, the nodes announce: “Yes, I have no other data on this event. The value “O” is the latest information we deserve. ”
In any other case, the nodes can answer “Node 1”: “Listen! I have more recent data on this transaction. Not "Oh," but something better. "
At the stage of voting, the nodes come to a decision: either everyone accepts the same value, or one of them votes against, indicating that he has more recent data. - If the round of voting was successful, and everyone was in favor, then the system moves to a new stage - acceptance of the value (Accept). “Node 1” collects all the responses of other nodes and reports: “Everyone agreed with the value“ O ”! Now I officially declare that “O” is our new meaning, the same for all! Write yourself in a booklet, do not forget. Write to your log! ”
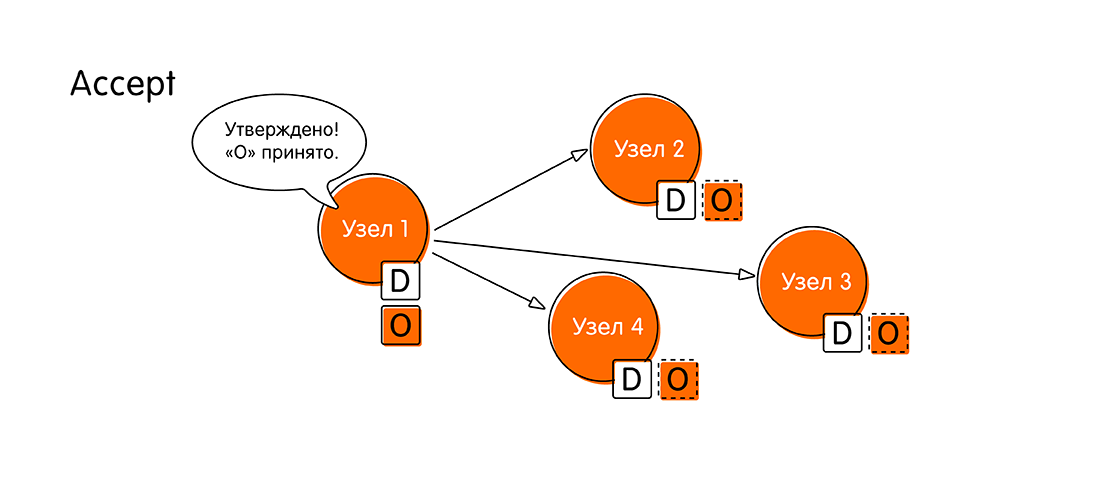
- The remaining nodes send a confirmation (Accepted) that they wrote down the value "O", they did not manage to do anything new during this time (a kind of two-phase commit). After this momentous event, we believe that the distributed transaction has completed.
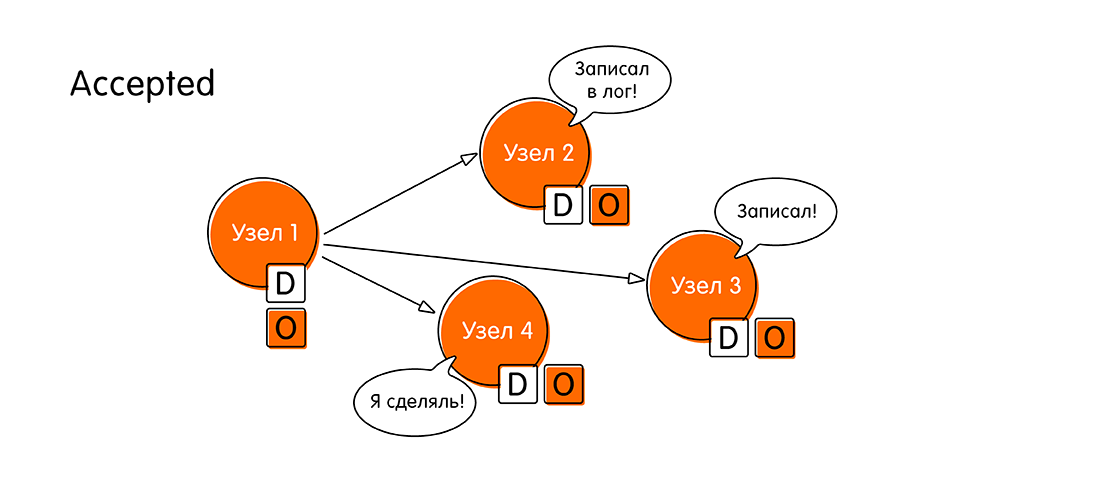
Thus, the consensus algorithm in the simple case consists of four steps: propose, voting, acceptance, confirmation of acceptance.
If at some step we could not reach agreement, then the algorithm is restarted, taking into account the information provided by the nodes that refused to confirm the proposed value.
Consensus Algorithm in an Asynchronous System
Before that, everything was smooth, because it was about a synchronous messaging model. But we know that in the modern world we are used to doing everything asynchronously. How does a similar algorithm work in a system with an asynchronous messaging model, where we believe that the time to wait for a response from a node can be arbitrarily long (by the way, the failure of a node can also be considered as an example when a node can respond for an arbitrarily long time) )
Now that we know how the consensus algorithm basically works, the question is for those inquisitive readers who have reached this point: how many nodes in a system of N nodes with an asynchronous message model can fail so that the system can still reach consensus?
The correct answer and rationale behind the spoiler.The correct answer is
0 . If at least one node in the asynchronous system fails, the system cannot reach consensus. This assertion is proved in the FLP theorem known in certain circles (1985, Fischer, Lynch, Paterson, link to the original at the end of the article): “The inability to achieve distributed consensus when at least one node fails”.
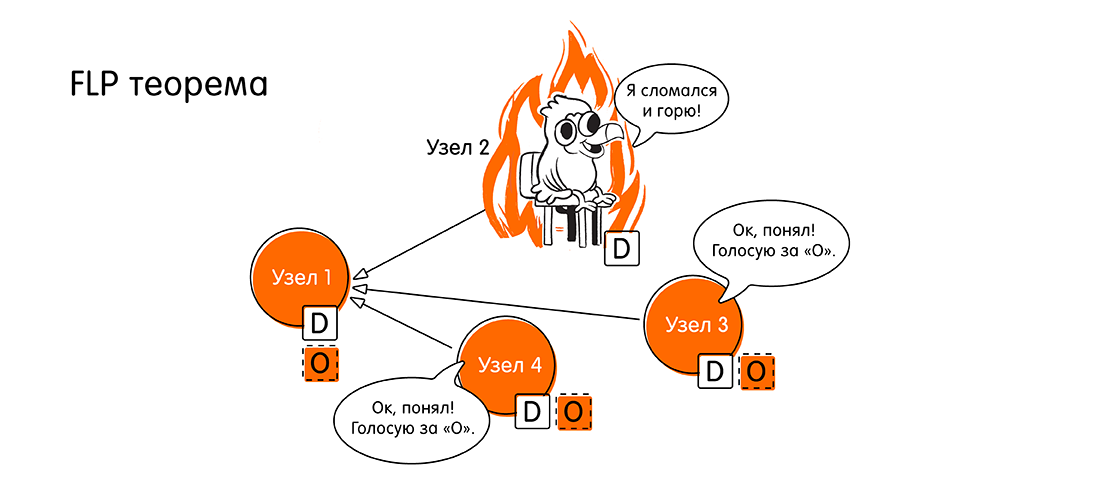
Guys, then we have a problem, we are used to the fact that everything is asynchronous with us. And here it is. How to live further?
We are now talking about theory, about mathematics. What does it mean, “consensus cannot be reached” when translating from a mathematical language to ours - engineering? This means that “can not always be achieved”, i.e. there is a case where consensus is not achievable. And what is this case?
This is just a violation of the liveness property described above. We do not have a general agreement, and the system cannot progress (cannot complete in a finite time) in the case when we do not have an answer from all nodes. Because in an asynchronous system we don’t have a predictable response time, and we can’t know if the node is down or just takes a long time to respond.
But in practice, we can find a solution. Let our algorithm work for a long time in case of failures (it can potentially work endlessly). But in most situations, when most nodes function correctly, we will have progress in the system.
In practice, we are dealing with partially synchronous communication models. Partial synchronicity is understood as follows: in the general case, we have an asynchronous model, but formally we introduce a certain concept of “global stabilization time” of a certain moment in time.
This point in time may not come arbitrarily long, but one day it must come. A virtual alarm will ring, and from now on we can predict the time delta for which messages will reach. From this moment, the system turns from asynchronous to synchronous. In practice, we are dealing with precisely such systems.
Paxos Algorithm Solves Consensus Issues
Paxos is a family of algorithms that solve the consensus problem for partially synchronous systems, provided that some nodes may fail. The author of Paxos is
Leslie Lamport . He proposed formal proof of the existence and correctness of the algorithm in 1989.
But the proof was by no means trivial. The first publication was released only in 1998 (33 pages) with a description of the algorithm. As it turned out, it was extremely difficult to understand, and in 2001 an explanation for the article was published, which took 14 pages. The volumes of publications are given in order to show that, in fact, the problem of consensus is not at all simple, and such algorithms are a huge work of the smartest people.
It is interesting that Leslie Lamport himself in his lecture noted that in the second article-explanation there is one statement, one line (did not specify which one), which can be interpreted differently. And because of this, a large number of modern Paxos implementations do not work correctly.
A detailed analysis of Paxos's work will draw more than one article, so I will try to convey the main idea of the algorithm very briefly. In the links at the end of my article you will find materials for further immersion in this topic.
Roles in Paxos
Paxos has a concept of roles. Let's consider three main ones (there are modifications with additional roles):
- Proposers (terms may also be used: leaders or coordinators) . These are the guys who learn about some new meaning from the user and take on the role of leader. Their task is to launch a round of proposals of a new significance and coordinate further actions of the nodes. Moreover, Paxos allows the presence of several leaders in certain situations.
- Acceptors (Voters) . These are the nodes that vote for the adoption or rejection of a particular value. Their role is very important, because the decision depends on them: in what state the system will go (or not) after the next stage of the consensus algorithm.
- Learners . Nodes that simply accept and record the new accepted value when the state of the system has changed. They do not make decisions, they simply receive data and can give it to the end user.
One node can combine several roles in different situations.
Quorum concept
We assume that we have a system of
N nodes. And from them a maximum of
F nodes can fail. If F nodes fail, then we must have at least
2F + 1 acceptor nodes in the cluster.
This is necessary so that we always, even in the worst situation, have a “good”, correctly working nodes majority. That is,
F + 1 “good” nodes that agreed, and the final value will be accepted. Otherwise, there may be a situation where we have different local groups will take on different meanings and will not be able to agree among themselves. Therefore, we need an absolute majority to win the vote.
The general idea of the Paxos consensus algorithm
The Paxos algorithm involves two large phases, which in turn are divided into two steps each:
- Phase 1a: Prepare . At the preparation stage, the leader (proposer) informs all nodes: “We are starting a new voting stage. We have a new round. The number of this round is n. Now we will begin to vote. ” For now, it simply reports the start of a new cycle, but does not report a new value. The task of this stage is to initiate a new round and tell everyone its unique number. The round number is important, it must be a value greater than all previous voting numbers from all previous leaders. Since it is precisely thanks to the round number that other nodes in the system will understand how fresh the leader has data. Other nodes probably already have voting results from much later rounds and they will simply tell the leader that he is behind the times.
- Phase 1b: Promise . When the acceptor nodes have received the number of the new voting stage, two outcomes are possible:
- The number n of the new vote is greater than the number of any of the previous votes in which the acceptor participated. Then the acceptor sends the leader a promise that he will no longer participate in any vote with a lower number than n. If the acceptor has already managed to vote for something (that is, in the second phase, he accepted some value), then he will attach the accepted value and the voting number in which he participated in his promise.
- Otherwise, if the acceptor already knows about the vote with a large number, he can simply ignore the preparation stage and not answer the leader.
- Phase 2a: Accept . The leader needs to wait for an answer from the quorum (most nodes in the system) and, if the required number of answers is received, then he has two options for the development of events:
- Some of the acceptors sent values for which they had already voted. In this case, the leader selects the value from the vote with the maximum number. We call this value x, and sends out to all nodes a message of the form: “Accept (n, x)”, where the first value is the voting number from its own Propose step, and the second value is what everyone gathered for, i.e. value for which, in fact, vote.
- If none of the acceptors sent any values, but they simply promised to vote in this round, the leader can offer them to vote for their value, then the value for which he generally became a leader. Call it y. He sends to all nodes a message of the form: "Accept (n, y)", by analogy with the previous outcome.
- Phase 2b: Accepted . Further, the acceptor nodes, upon receipt of the “Accept (...)” message, from the leader agree with him (send confirmation to all nodes that they agree with the new value) only if they have not promised any (to another) leader to vote with a round number n '> n , otherwise they will ignore the confirmation request.
If the majority of nodes answered the leader, and all of them confirmed the new value, then the new value is considered accepted. Hooray! If the majority is not typed or there are nodes that refused to accept the new value, then everything starts all over again.
This is how the Paxos algorithm works. Each of these stages has many subtleties, we practically did not consider various types of failures, problems of multiple leaders and much more, but the purpose of this article is only at the top level to introduce the reader to the world of distributed computing.
It is also worth noting that Paxos is not one of a kind, there are other algorithms, for example,
Raft , but this is a topic for another article.
Links to materials for further study
Beginner Level:
Leslie Lampport Level:
- Impossibility of Distributed Consensus with One Faulty Process (FLP impossibility) , Fischer, Lynch and Paterson, research paper, 1985
- The Part-Time Parliament , Leslie Lamport, research paper, 1998
- Paxos made simple , Leslie Lamport, research paper, 2001