
Thousands of years ago, mankind became acquainted with amazing materials that have found their application in various fields of life. These were metals. Since we often can’t just use what the planet gives us, many great minds have come up with various ways of strengthening / hardening metals. But everything has its own limit, and it was considered impossible to overcome certain limitations of the crystal structure of metals regarding dislocations. Today we will get acquainted with a study in which scientists from the University of Wisconsin in Madison (USA) demonstrated that it was time to rewrite the previously established rules regarding metals. What exactly was possible to do with the crystalline structure of the metal, why is the fixation of dislocations not so simple, and what kind of buns are hidden in this study for humanity? We learn about this from the report of scientists. Go.
Study basis
Forge the iron, without departing from the cash register. Several physical terms are hidden in this metaphor at once, one of which is malleability - a property of a material that determines its ability to be processed by deformation, i.e. forged. For metals, ductility is a kind of indicator of ductility. It is this indicator that suffers the most in the case of strengthening the strength of the metal, because of which, at a certain critical moment, it can simply crack. In this study, scientists created a technique to forget about this problem, but about it a little later.
At the beginning of the last century, scientists realized that bending a metal is much easier than bending its molecular structure, which is most often a three-dimensional lattice. Nothing is perfect and everything has defects, even the crystal lattice of a solid. They are called dislocations. These lattice inaccuracies are sufficiently mobile, which allows metals to be so malleable. If we want to harden the metal, then dislocations cannot be touched, they are untouchable, at least as previously thought.
In the work we are considering today, scientists were able to obtain a high degree of plastic deformation for
intermetallic * without the aid of dislocations.
Intermetallic * - a compound of two or more metals.
It is worth noting that its grains (crystallites) play an important role in the mechanical properties of metals. If the grains are small in size, then the main mechanism of deformation is the sliding / displacement of grain boundaries. If the grains are large, then the metal is deformed by direct amorphization along the shear plane.

Strengthening the metal is achieved in various ways, the most effective of which is the change in grain size. The smaller the grain, the stronger the metal. More scientifically, this can be expressed as the Hall-Petch law (or the Hall-Petch relation). The effect of this law comes into force when the movement of dislocations along grain boundaries is blocked. However, scaling the strength depending on the grain size described by this law can destroy metals with a face-centered crystal lattice.
 Scheme of face-centered lattice.
Scheme of face-centered lattice.Also, this law cannot be applied endlessly, because when the grain size is less than 12-15 nm, the strength of the metal does not increase, as the Hall-Petch law suggests, but rather decreases. This phenomenon is called the inverse Hall-Petch law.
Researchers do not deny that the fixation of dislocations allows hardening of the metal, but this has a tangible negative effect on its ductility. It is for this reason that the study of other mechanisms for the placement of deformations, besides dislocations, may open up new possibilities for the construction of materials with unique mechanical properties.
In their work, scientists conducted modeling and practical experiments using samarium pentacobalt (SmCo
5 ) - an intermetallic compound consisting of cobalt and samarium. They managed to prove that plastic deformation without an emphasis on dislocations is not only possible, but also quite easily achievable.
Research results
Before testing everything in practice, scientists conducted a simulation using the
embedded atom model (
EAM ), adapted to many properties of Sm, Co and Sm – Co. In the calculations, different grain sizes were taken into account: from 5 nm to 65 nm. Each of the studied samples in the model contained 10 grains with a random orientation. The grain size during the transition from sample to sample changed, but the orientation remained the same. Scientists have created models of uniaxial tension and uniaxial compression at a strain rate of 10
8 s
-1 .
 Image No. 1
Image No. 1Graphs
1a and
1b show the results of compression modeling. It was found that the conservation of plasticity is maintained up to grain sizes of 37 nm. In the case of larger grains, an increase in stress is observed, but no signs of the Hall-Petch ratio.
For comparison, scientists conducted a tensile simulation for copper (Cu), during which signs of the Hall-Petch relation and the inverse Hall-Petch ratio for grains less than 12 nm were clearly visible.
At the same time, SmCo
5 samples show a clear plastic deformation for all grain sizes without voids or cracks, even if the true deformation reaches 18%.
To confirm the simulation results, the researchers measured the microhardness of SmCo
5 samples with different grain sizes. A difference was found in the results of the measured dependence of hardness on grain size (
1c ) and the dependence of strength on grain size (
1b ) obtained during simulation. Due to the fact that approximate proportionality of microhardness and strength is expected, it can be said that the experiments confirmed the simulation results.
It was also found that the strength of SmCo
5 (~ 2 GPa with a grain size of 12 nm) is comparable to the strength of the hcp (hexagonal close-packed) lattice Co.
In HCPs (face-centered) and HCPs (close-packed hexagonal) metals, the enhancement of grain boundaries with a decrease in grain size is explained by a decrease in the number of dislocations formed in the boundaries in fine-grained materials.
In the models presented in the study, no slip of dislocations was observed, and this is consistent with the relatively high energy barriers for the nucleation and motion of dislocations found in calculations of the potential energy surface (PES) of a hard slip.
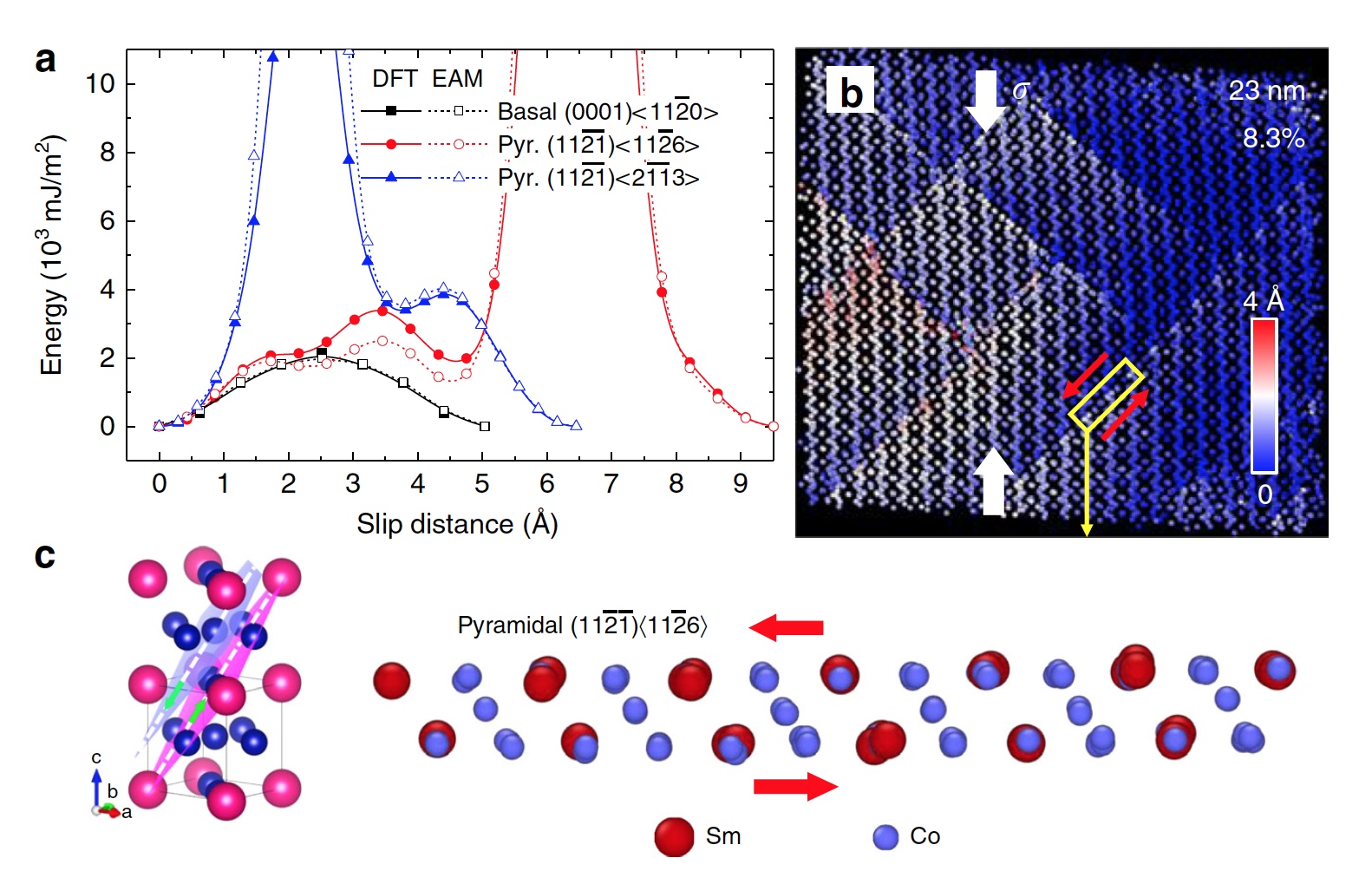 Image No. 2
Image No. 2Figure
2a shows examples of PES calculated using the density functional theory (DFT) and the immersed atom model (EAM). Scientists note that despite the lack of a direct relationship between potential and PES, both methods gave very similar results.
The lowest EM score, i.e. energy maximum, (1982 mJ / m
2 ) was observed for basal slip [(0001) ⟨1120⟩]. The pyramidal 2
s +
a slip [(1121) ⟨1126⟩] has a comparable EM at the initial slip stage, but the actual EM arising at a slip distance of 6.5 Å is very high (65280 mJ / m
2 ). The pyramidal
c +
a slip [(1121) ⟨2113⟩] demonstrates EM (29680 mJ / m
2 ) immediately at the beginning of the slip.
The most important observation, according to the researchers, is that for SmCo
5 even the lowest EM is one order of magnitude higher than the values calculated for ordinary hcp metals.
In addition, the energy introduced into the crystal by the dislocation is proportional to
b 2 , where
b is the length
of the Burgers vector * . The
b values for dislocations in SmCo
5 are above 5 Å, i.e. significantly higher than, for example, the value of 2.55 Å for Cu [(111) ⟨110⟩] and 3.21 Å for slip systems Mg [(0001) ⟨1120⟩].
Burgers vector * - quantitatively describes the distortion of the crystal lattice around the dislocation.
Although complete dislocation glide was not observed during the experiments, there were signs of partial slip on the pyramidal system 2c +
a (
2b ). The nature of this partial slip can be understood if we pay attention to the PES in graph
2a . At the beginning of the slip, the energy is quite low, and the slip stops at a distance of less than ~ 1.5 Å, because it collides with a high EM.
In image
2b , incomplete pyramidal slides are shown, and in
2c the same is shown, but at the atomic level.
The slip distance observed during the simulation is much shorter than the length of the Burgess vector, which is 9.5 Å.
Basal glide was not detected. This may have the following explanation: the probability that a single basal plane will have the greatest shear stress is less than the probability that one of the three planes for 2
s +
a slip will have a shear stress high enough to initiate a slip (
2c ), even if the basal glide has the lowest EM.
Obviously, SmCo
5 does not have five independent slip systems of dislocations (in fact, they are not at all) that can continue to adapt to deformation, guaranteeing arbitrary plastic deformation of the polycrystal. Materials of this kind are usually very fragile, but not in this case, since the modeling clearly showed a high degree of ductility.
 Image No. 3
Image No. 3During modeling and calculations, it was found that the ductility of SmCo
5 is due to the sliding of grain boundaries and direct amorphization along the shear plane. Scientists called the structures obtained as a result of such processes amorphous
shear bands * .
Shear band * - area of local deformation in a metal or alloy.
Most often, so-called accommodation mechanisms are necessary for the occurrence of boundary sliding in polycrystalline materials, i.e. mechanisms that relieve the stress accumulated in a triple joint (like a tee in geology) due to the sliding of adjacent grain boundaries (
3a -
3d ).
When the shear stress of the boundary exceeds its strength, the very sliding of the boundary (
3a ) and the accumulation of local stress in the ternary compound (
3b ) occur. Local stress resists further sliding along the boundary and begins to grow with increasing stress. At the moment of reaching the critical point, the stress leads to the formation of an amorphous shear band from the ternary compound (
3c ). Due to the fact that heterogeneous nucleation releases local stress (
3d ), the sliding of the boundaries continues. During this process, sudden softening is observed, and after that - voltage stabilization. Similar processes were observed both for tensile deformation and for compression.
To confirm the amorphism of the regions inside the slip, the
pair distribution functions (
PDF -
pair distribution function ) of Co-Co and Sm-Sm in local grain regions were calculated. The calculation results were compared with those for a single crystal and amorphous mass (
3e ,
3f ).
A comparative analysis of the calculations showed that for samples deformed under compression to 9.4%, the peaks in the PDF of the crystalline zone are wider and lower due to local distortions, but nevertheless have a clear similarity with those in a single crystal. But the PDFs calculated within the shear band perfectly coincide with those for the bulk amorphous SmCo
5 sample, and the dependence of PDF on the grain size was not detected at all.
Next, scientists had to check their predictions that SmCo
5 could undergo significant plastic deformation. For this, experiments were conducted during which samples in the form of micro-columns were subjected to deformation.
It was found that SmCo
5 samples actually deform plastically and do not collapse when exposed to more than 20% stress. Next, high resolution transmission electron microscopy (HRTEM) was used on a SmCo
5 sample that was deformed by pressure. This made it possible to verify the theory of amorphous shear bands caused by stress. Microscopy confirmed the presence of several shear bands in the deformation region (
3g ). The most curious thing is that no dislocations were found in the study area.
The FFT (fast Fourier transform) and inverse FFT graphs showed that the shear band is amorphous, while the out-of-band regions are crystalline (
3h -
3j ). It was also found that amorphous shear bands propagate in grains without cracking.
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the
report of scientists and
additional materials to it.
Epilogue
In this work, researchers were able to successfully demonstrate their theory in practice - the world did not converge in dislocations on dislocations. For many years, scientists believed that dislocations should be mobile, which will allow the metal to be ductile and not break at the slightest stress. However, this statement is erroneous, which was confirmed by the study we examined today.
In the future, scientists from the University of Wisconsin intend to continue the study of metals, concentrating on the search for their hidden properties. Perhaps these properties are not so hidden, maybe just a previously established erroneous statement directed us in the wrong direction of searches? Maybe so, maybe researchers will be able in the future to debunk a couple more “axioms” from the world of materials science. It’s not for nothing they say, trust - but check.
Thank you for your attention, remain curious and have a good working week, guys! :)
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending it to your friends, a
30% discount for Habr users on a unique analogue of entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to divide the server? (options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Dell R730xd 2 times cheaper? Only we have
2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - from $ 99! Read about
How to Build Infrastructure Bldg. class c using Dell R730xd E5-2650 v4 servers costing 9,000 euros for a penny?