
One of the most important tasks in machine learning is Object Detection. Recently, a series of machine learning algorithms based on Deep Learning for object detection have been published. These algorithms occupy one of the central places in practical computer vision applications, in particular, the currently very popular Self-Driving Cars. But all these methods are teaching methods with a teacher, i.e. they need a huge dataset (huge dataset). Naturally, there is a desire to have a model capable of learning from “raw” (unallocated) data. I tried to analyze existing methods and also indicate possible ways of their development. I ask everyone who wishes mercy under kat, it will be interesting.
Current status of the question
Naturally, the formulation of this problem has existed for a long time (almost from the first days of the existence of machine learning) and there is a sufficient number of works on this topic. For example, one of my favorite
Spatially Invariant Unsupervised Object Detection with Convolutional Neural Networks . In short, the authors are training Variable Auto Encoder (VAE), but this approach raises a number of questions for me.
A bit of philosophy
So what is an object in an image? To answer this question, we must answer the question - why do we even divide the world into objects? After a little reflection on this question, I had only one answer to this question (I’m not saying that there are no others, I just didn’t find them) - we are trying to find a representation of the world that is easy for us to understand and control the amount of information needed to describe the world in the context of the current task. For example, for the task of classifying images (which is generally formulated incorrectly - there are very rarely images with one object. Ie, we solve the problem not what is shown in the picture, but which object is “main”), we just need to say that the picture is “car” In turn, for the task of detecting objects, we want to know what “interesting” objects (we are not interested in all the leaves from the trees in the picture) are there, and where they are, for the task of describing the scene, we want to get the name of the “interesting” process it happens there, for example, "sunset", etc.
It turns out that objects are a convenient representation of data. What properties should this representation have? The view should contain as much as possible complete information about the image. Those. having an object description, we want to be able to restore the original image with the necessary degree of accuracy.
How can this be expressed mathematically? Imagine that the image is a realization of a random variable X, and the representation will be a realization of a random variable Y. In view of the above, we want Y to contain as much information as possible about X. Naturally, to do this, use the concept of mutual information.
Machine learning models for maximum information
Detection of objects can be considered as a generative model, which receives an image at the input
, and the output is an object representation of the image
.

Let's now recall the formula for calculating mutual information:
Where
joint density distribution as well
marginalized.
Here I will not go deep why this formula looks like this, but we will believe that internally it is very logical. By the way, based on the described considerations, it is not necessary to choose exactly mutual information, it can be any other “information”, but we will come back to this closer to the end.
Particularly attentive (or those who read books on the theory of information) have already noticed that mutual information is nothing more than the Kullback-Lebler divergence between the joint distribution and the work of marginal ones. Here a slight complication arises - anyone who has read at least a couple of books on machine learning knows that if we only have samples from two distributions (i.e. we don’t know the distribution functions), then it’s not even optimizing, but even evaluating Kullback’s divergence, Leibler's task is very non-trivial. Moreover, our beloved GANs were born precisely for this reason.
Fortunately, the wonderful idea of using the lower variational boundary described in
On Variational Bounds of Mutual Information comes to our aid. Mutual information can be represented as:
Or
Where
- the distribution of the representation for a given image, parameterized by our neural network and from this distribution we are able to sample, but we do not need to be able to evaluate the density or probability of a particular sample (which is generally typical of many generative models).
Is a certain density function parametrized by the second neural network (in the most general case, we need 2 neural networks, although in some cases they can be represented by the first one), here we must be able to calculate the probabilities of the resulting samples.
Value
called the Lower Variational Bound.
Now we can solve the approach to our problem, namely, to increase not the mutual information itself, but its lower variational boundary. If the distribution
chosen correctly, then at the maximum point of the variational boundary and mutual information will coincide, but in the practical case (when the distribution
cannot imagine exactly
, but consists of a fairly large family of functions) will be very close, which also suits us.
If someone does not know how this works, I advise you to very carefully deal with the EM algorithm. Here is a completely similar case.
What is going on here? In fact, we got the functionality for training the auto encoder. If Y is the result at the output of a neural network with some picture at the input, then this means that
where
neural network transformation function. And approximate the inverse distribution by Gaussian, i.e.
we get:
And this is a classic feature for auto encoder.
Auto Encoder is not enough
I think that many already want to train the auto-encoder and hope that in its hidden layer there will be neurons that respond to specific objects. In general, there is confirmation of something similar and it turns out
Building High-level Features Using Large Scale Unsupervised Learning . But still this is completely impractical. And the most attentive people have already noticed that the authors of this article used regularization - they added a term that provides sparseness in the hidden layer, and they wrote in black and white that nothing of the sort happens without this term.
Is the principle of maximizing mutual information enough to learn a “convenient” idea? Obviously not, because we can choose Y equal to X (that is, use the image itself as its representation) or any bijective transformation, mutual information goes to infinity in this case. There can be no more of this value, but as we know this is a very poor idea.
We need an additional criterion for the “convenience” of presentation. The authors of the above article took sparseness as "convenience." This is a kind of realization of the hypothesis that there should be a few “important objects” in the picture. But we will go further - we want to not only know the fact that such an object is in the picture, but also want to know where it is, how much it is overlapped, etc. The question arises, how to make the neural network interpret the output of a neuron such as, for example, the coordinate of an object? The answer is obvious - the output from this neuron should be used precisely for this. That is, knowing the idea, we must be able to generate “similar” pictures to the original one.
The general idea was borrowed from the guys from Facebook.
The encoder will look like this:

Where
- some vector describing the object,
- coordinates of the object,
- the scale of the object,
- the position of the object in depth,
- the probability that the object is present.
That is, the input neural network receives a picture of a predetermined size on which we want to find objects and issues an array of descriptions. If we want a single-pass network, then unfortunately this array will have to be fixed size. If we want to find all the objects, then we will have to use recruitment networks.
The decoder will be like this:
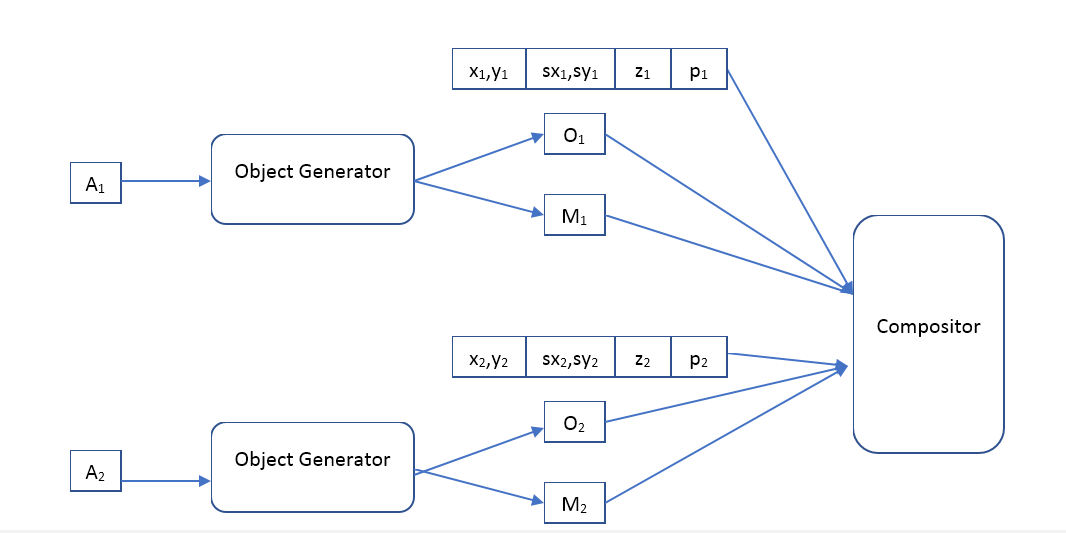
Where Object Generator is a network that receives an object description vector at the input and gives
- the image (of a certain standard size) of the object and the mask of opaque pixels (opacity mask).
Compositor - receives the input image of all objects, mask, position, scale, depth and forms the output image, which should be similar to the original.
What is the difference between our approach and VAE?
It seems that we want to use an auto encoder with the same architecture as the authors of the
Spatially Invariant Unsupervised Object Detection with Convolutional Neural Networks article, so the question is what is the difference. Both there and there is an auto-encoder, only in the second version it is variational.
From a theoretical point of view, the difference is very large. VAE is a generative model and its task is to make 2 distributions (source and generated images) as similar as possible. Generally speaking, VAE makes no warranties that the image generated from the “description” of an object generated from the original image will be at least slightly similar to the original. By the way, the authors of VAE
Auto-Encoding Variational Bayes themselves speak about this. So why does it still work? I think that the selected architecture of the neural networks and the “description” helps to increase the mutual information of the image and the “description”, but I could not find any mathematical evidence for this hypothesis. A question for readers, can someone be able to explain the results of the authors - their restored image is very similar to the original, why?
In addition, the use of VAE forces authors to specify the distribution of “descriptions,” and the method of maximizing mutual information makes no assumptions about this. Which gives us additional freedom, for example, we can try to cluster vectors on an already trained model
descriptions, and look - maybe such a system will learn the classes of objects? It should be noted that such clustering using VAE makes no sense, for example, the authors of the article use a Gaussian distribution for these vectors.
The experiments
Unfortunately, now the work takes a huge amount of time and it is not possible to complete it in an acceptable amount of time. If someone wants to write several thousand lines of code, train hundreds of machine learning models and conduct many interesting experiments, simply because he (or she) enjoys it, I will be glad to join forces. Write in a personal.
The field for experiments here is very wide. I have plans to start by teaching the classic auto-encoder (deterministic mapping of images to descriptions and a Gaussian inverse distribution) and see what it learns. In the first experiments, it will be sufficient to use the composer described by the guys from Facebook, but in the future I think it will be very interesting to play with various composers, and it is possible to make them also learnable. Compare different regularizers: without it, Sparse, etc. Compare use of feedforward versus recursive models. Then use more advanced distribution models for inverse distribution, for example, such a
Density estimation using Real NVP . See how better or worse it gets with more flexible models. See what will happen if the display of images on descriptions is made non-deterministic (generated from some conditional distribution). And finally, try to apply different clustering methods to description vectors
and understand whether such a system can learn object classes.
But most importantly, I really want to compare the quality of the model based on maximizing mutual information and the model with VAE.