Hi Habr.
In the process of studying neural networks, the idea arose of how to apply them for something almost interesting, and not as hackneyed and trivial as the ready datasets from MNIST. For example, why not recognize Morse code.

No sooner said than done. For those who are interested in how to create a working CW decoder from scratch, details are under the cut.
To begin with, I will answer the question, but why the neural network itself. Firstly, just out of interest, the project is more likely to be educational, rather than commercial, and secondly, the real signal when passing through the atmosphere is rather distorted, and the output is not quite what is in the picture of dots and dashes. Here is an example of real envelopes of the same letter "C", recorded from the air:
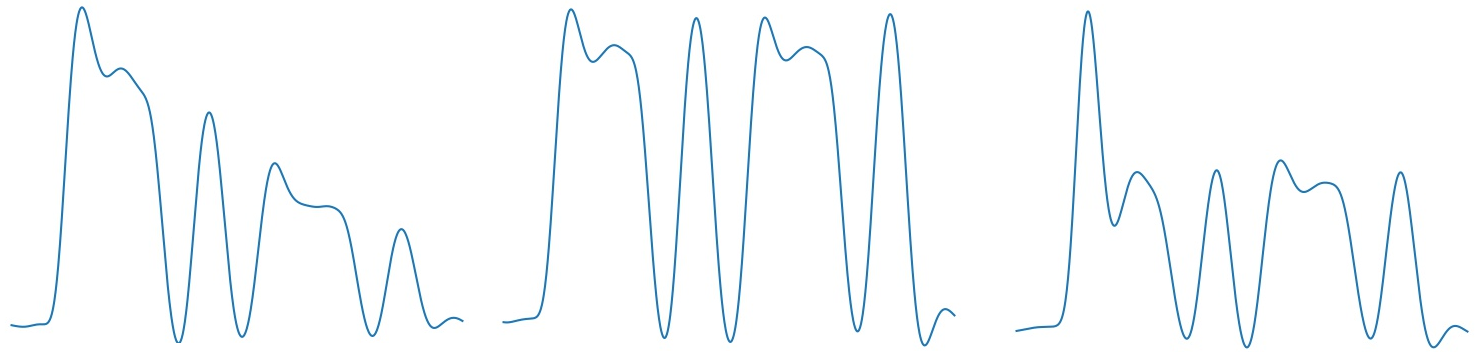
And this is a rather strong signal, but a weak one can have anything at all. In general, for such fuzzy data here, the neural networks are just quite interesting and promising. So far, programs that recognize Morse code are better than a professional radio operator among whistlers, noises and interference, as far as I know, do not exist, and I'm 95% sure that if such a thing appears, then AI approaches will be used there.
Anyone can repeat the experiments described below, for this you do not even need to have a radio receiver. All source files were recorded via
websdr , where you can easily hear ham, for example at frequencies of 7 and 14 MHz. There is also a Record button with which any signal can be recorded in wav format.
Isolation of a signal from a recording
In order for a neural network to recognize Morse code symbols, they must first be selected from the original record.
Download the data from the wav file and display it on the screen.
from scipy.io import wavfile import matplotlib.pyplot as plt file_name = "websdr_recording_2019-08-17T16_26_52Z_14026.0kHz.wav" fs, data = wavfile.read(file_name) plt.plot(data) plt.show()
If everything was done correctly, we will see something like this:
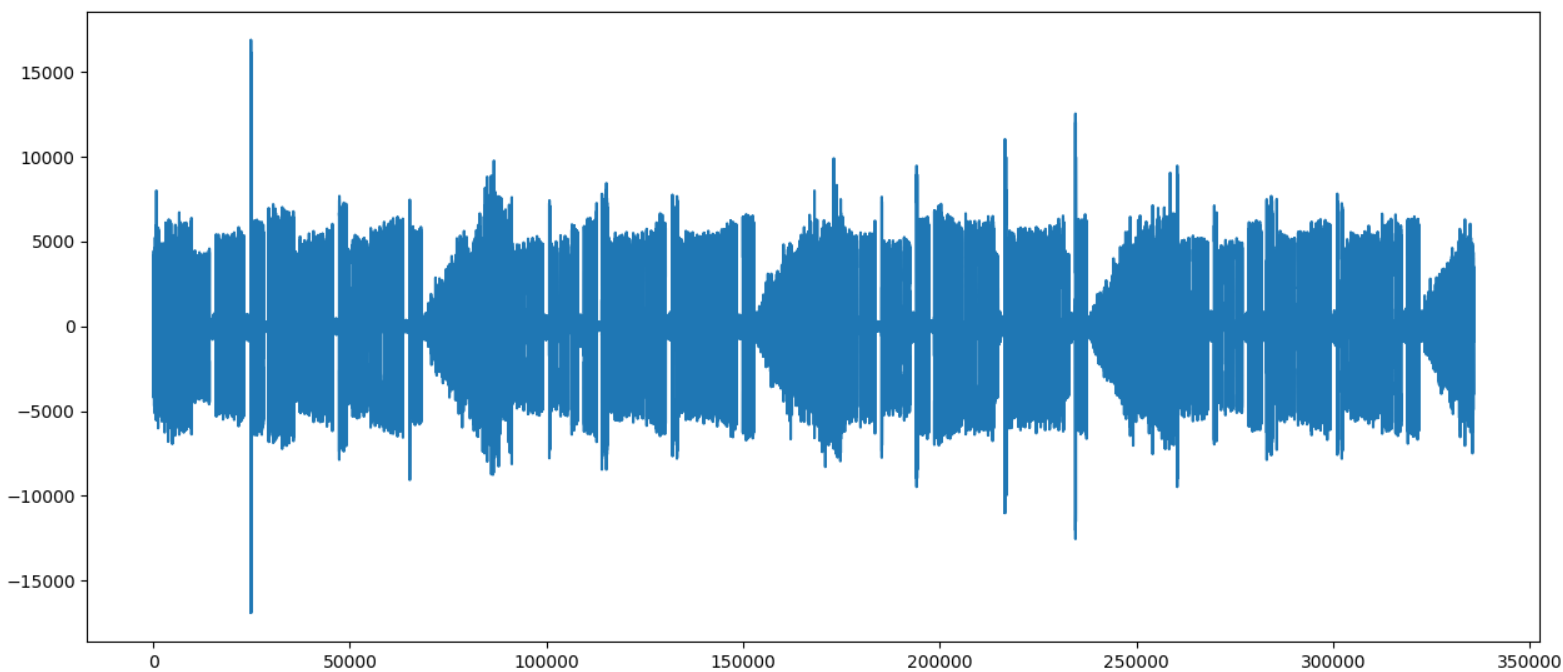
Historically, a Morse code signal is the simplest type of modulation that you can think of - the tone is either there or not. Therefore, in the record there can be several signals at the same time, and they do not interfere with each other.

When recording CW signals, I set the frequency to 1 KHz lower and the Upper Side Band mode, so that the signal of interest to us is always in the recording at a frequency of 1 KHz. Select it using a band-pass filter (Butterworth filter).
from scipy.signal import butter, lfilter, hilbert def butter_bandpass(lowcut, highcut, fs, order=5): nyq = 0.5 * fs low = lowcut / nyq high = highcut / nyq b, a = butter(order, [low, high], btype='band') return b, a def butter_bandpass_filter(data, lowcut, highcut, fs, order=5): b, a = butter_bandpass(lowcut, highcut, fs, order) y = lfilter(b, a, data) return y cw_freq = 1000 cw_width_hz = 50 data_filtered = butter_bandpass_filter(data, cw_freq - cw_width_hz, cw_freq + cw_width_hz, fs, order=5)
We apply the Hilbert transform to the resulting signal to obtain the envelope.
def hilbert_envelope(data): analytical_signal = hilbert(data) amplitude_envelope = np.abs(analytical_signal) return amplitude_envelope y_env = hilbert_envelope(data_filtered)
As a result, we get a quite recognizable Morse code signal:
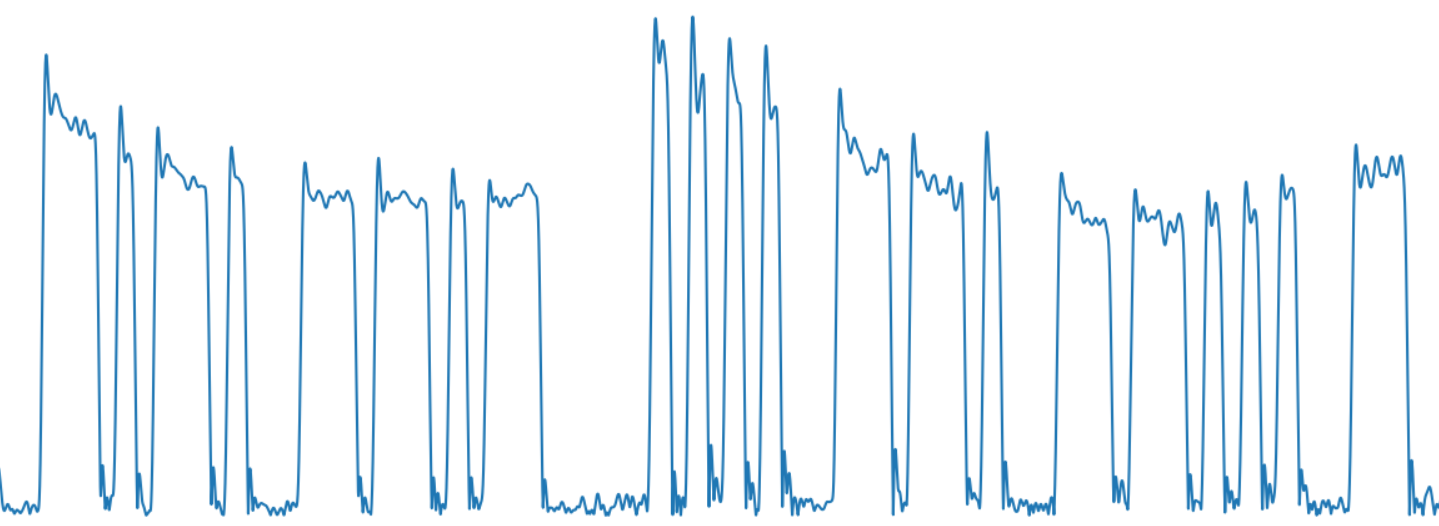
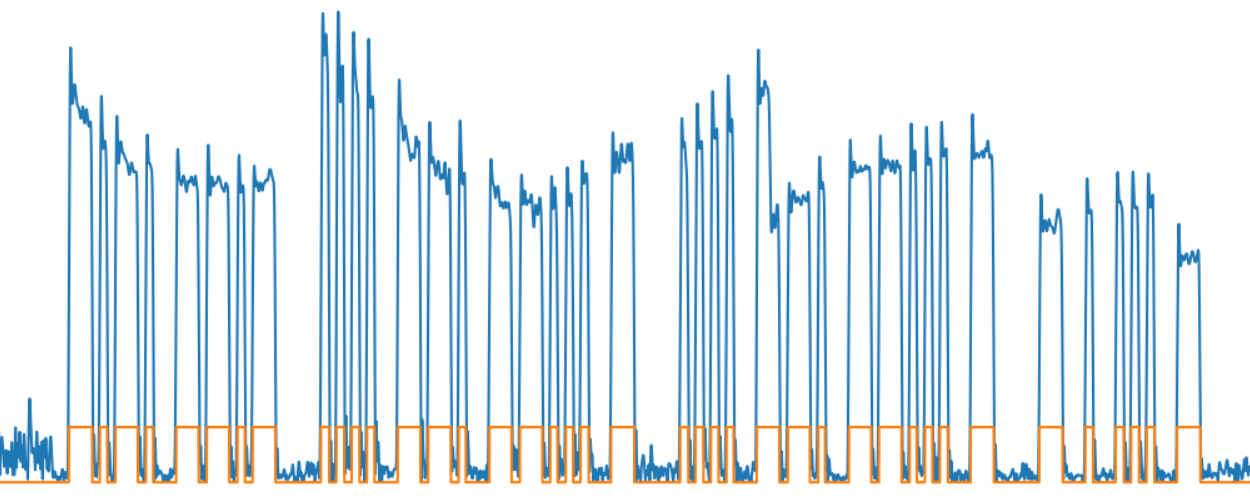
The next task is to highlight individual characters. The difficulty here is that the signals can be of different levels - as can be seen in the picture, due to the propagation in the atmosphere, the signal level “floats”, it can decay and amplify again. So just trimming data at a certain level would not be enough. Use a moving average and a low pass filter to get a very smooth current signal average.
def moving_average(a, n=3): ret = np.cumsum(a, dtype=float) ret[n:] = ret[n:] - ret[:-n] return ret[n - 1:] / n def butter_lowpass_filter(data, cutOff, fs, order=5): b, a = butter_lowpass(cutOff, fs, order=order) y = lfilter(b, a, data) return y ma_size = 5000 y_env2 = y_env
As you can see from the picture, the result is quite adequate to the signal change:
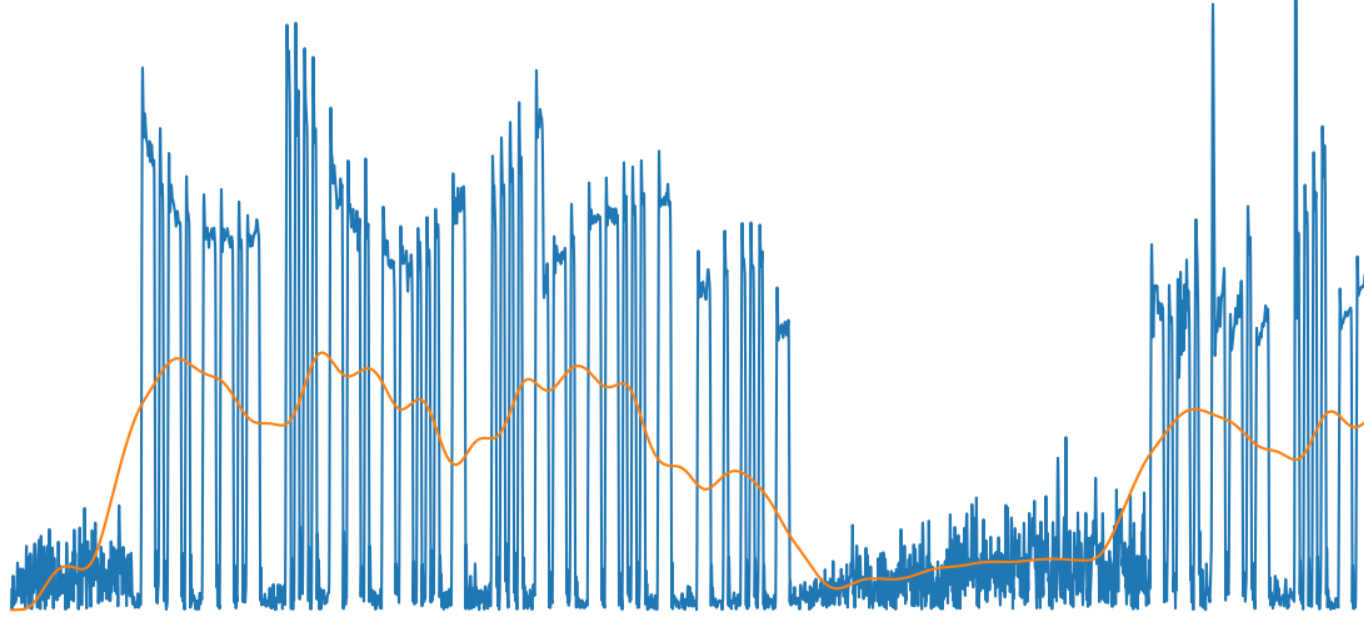
And finally, the last: we get a bitmap showing the presence or absence of a signal - we consider the signal to be “unity” if its level is above average.
y_normalized = y_ma3 < y_env2 y_normalized2 = y_normalized.astype("int16")
We moved from a noisy and uneven in level input signal to a noticeably more convenient digital signal for processing.
Character Highlighting
The next task is to highlight individual characters, for this you need to know the transmission speed. There are certain rules for correlating the duration of dots, dashes and pauses in Morse code (more
here ), to simplify, I simply set the duration of the minimum pause in milliseconds. In general, the speed can vary even within the limits of one record (at least
two subscribers participate in the broadcast, the settings of the transmitters of which may differ). The speed can also vary greatly for different recordings - an experienced radio operator can transmit 2-3 times faster than a beginner.
Then everything is simple, the code does not claim to be beautiful and elegant, but it works. We distinguish the rise and fall of the signals, and depending on the length, we separate the words and symbols.
Character Highlighting min_len = 0.05 symbols = [] pos_start, pos_end, sym_start = -1, -1, -1 data_mask = np.zeros_like(y_env2)
This is a temporary solution because ideally, speed should be determined dynamically.
The green line in the picture shows the envelope of the selected characters and words.

As a result of the program, we get a list, each element of which is a separate character, it looks something like this.

These data are already quite sufficient to process and recognize them by a neural network.
The text is long enough, so the continuation (it is the end) in the second part.