Mathematicians have proved that a random process when applied to a random surface invariably gives rise to certain patterns
 In the original article, this is a three-dimensional image that can be twisted
In the original article, this is a three-dimensional image that can be twistedIn the
film about the search for the lost Ark, Indiana Jones had to look for a secret room hiding the legendary
Ark of the Covenant . To determine its exact location, Indiana needed to find a special map, visible only when the sun shines through a special crystal in a certain room at a certain time of the day.
A similar idea - that the most important information can be disclosed only with the exact coincidence of certain circumstances - is found in many myths. It occurs in mathematics, sometimes in unexpected situations. Now,
three mathematicians have proved that if a certain type of randomness is very precisely tuned, then intricate geometric shapes appear - like a map with a treasure on a regular floor.
These pieces are similar to chess cells scattered over grids, which in turn are themselves created by a random process. One would think that piling randomness into randomness, we get confusion. It turns out that, as in the case of snowflakes, when each of them is unique, but at the same time they are all snowflakes, the mess converges to a universal form - if only the conditions turn out to be exactly as needed.
A turning point
Everyone knows that mathematicians study forms. Most of these forms follow deterministic rules: if I give you instructions for building a sphere, you will receive the same sphere every time.
But even mathematicians study the forms obtained as a result of random processes, such as, for example,
random walk - a path, the direction of each step of which is chosen randomly. In addition to random walks, there are other types of random geometric objects, for example, random two-dimensional surfaces (imagine a landscape where hills and valleys are scattered randomly) and random maps (a set of random points connected by lines).
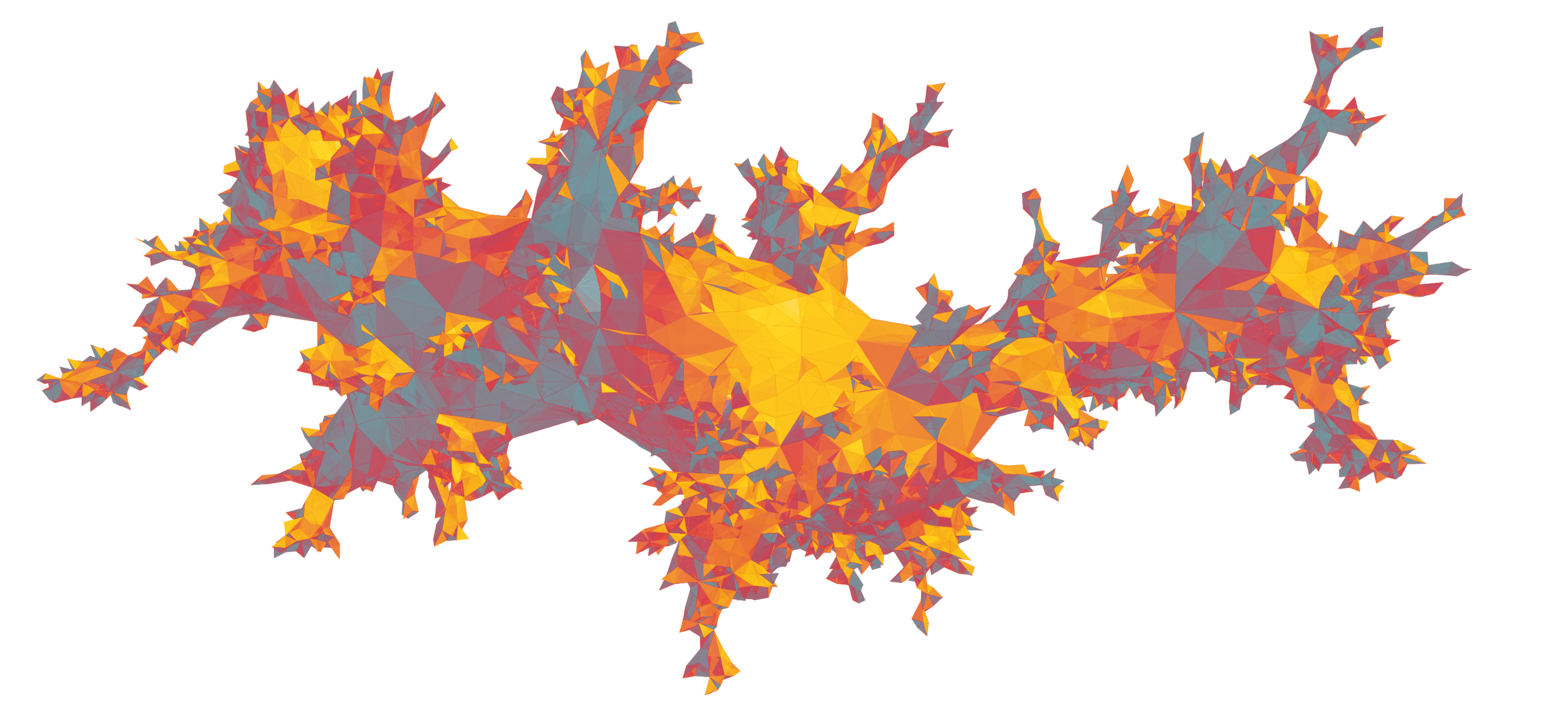 Random surface obtained by gluing triangles
Random surface obtained by gluing trianglesAll such forms are different from each other. However, mathematicians have found that these random processes converge to certain canonical forms. For example, all random walks are a form of
Brownian motion with a rather long walk. In recent years, mathematicians have discovered canonical forms and other random processes - and received the highest awards for this in their fields.
The new evidence is related to an understanding of the underlying properties of another random process.
It begins by creating a random surface. First you need to glue the triangles together. Then they need to be matched together in any way, only so that the resulting form is closed, like a package on a gift (no holes). If you start with a certain number of triangles on your hands, you will have many opportunities. Some of these “triangulations” will produce almost smooth, ball-like surfaces. Most of them will look more rough - like extreme surfaces resembling mountain ranges.
“It will not look like a regular sphere, it will have such large spikes,” said
Olivier Bernardi , a mathematician from Brandeis University, co-author of the work, which also involved
Nicholas Curien from the University of Paris-South XI and
Gregory Mjermont from the Higher Normal School in Lyon.
 Olivier Bernardi, Nicholas Curien and Gregory Myermont
Olivier Bernardi, Nicholas Curien and Gregory MyermontMyermont and another mathematician,
Jean-Francois le Gall , established many properties of these random triangulations in their previous work. The new proof goes even further by adding a second layer of randomness on top of random triangulation.
To add a new randomness, mark each point at which the triangles meet at the corners - what mathematicians call a vertex. Color the vertices randomly in black or white. You can do this by tossing a coin, although the coin may not be completely honest, and outweigh on one side.
Having painted the peaks, you can ask various questions about the pattern you created. One of the basic ones: how far can you go along the surface using only one black vertex? The process of moving along connected vertices of the same color is called seepage. This is a mathematical way to study a physical phenomenon of the same name as a fluid passes through a porous medium.
It will be easy to infiltrate (or not), depending on how the weight of the coin is distributed: if a coin tends to give out black vertices, infiltration is almost guaranteed; if for the extradition of whites, seepage will almost certainly be impossible.

Bernardi, Curien and Myermont study cases that fall between these extremes - a turning point in the change in the weight of the coin, when leakage turns from almost impossible to almost guaranteed phenomenon. They call this point a "critical threshold." This is an example of a phase transition, that magical moment when hot water suddenly becomes steam.
“The critical threshold means that if I slightly shift my parameters, then the behavior of my system will change from dramatic to dramatic with a different sign,” said Curien.
Physicists are interested in phase transitions because many of the most important natural phenomena occur just on the brink. Mathematicians are also interested in phase transitions, since important mathematical properties often appear just at these points.
“We know that water boils at 100 degrees, creating all these crazy patterns, and steam forms,” said
Scott Sheffield , a mathematician at MIT. “Sometimes such crazy and wild behavior becomes very interesting. This phase transition calls us to understand it. ”
In the new work, three mathematicians prove that such insane behavior manifests itself precisely in the phase transition of leakage. They show that at this critical threshold a geometric form appears - unique, and at the same time universal.
Hidden order in chance
The first part of the work determines how to correct a coin so that the coloring of the vertices falls on the threshold between the presence and absence of seepage. Confirming intuition, they prove that the ideal coin is the critical value - giving a 50% chance of falling black, and 50% of falling white.
“This is the first part of the work. We prove that exactly half happens, something interesting happens, ”Bernardi said.
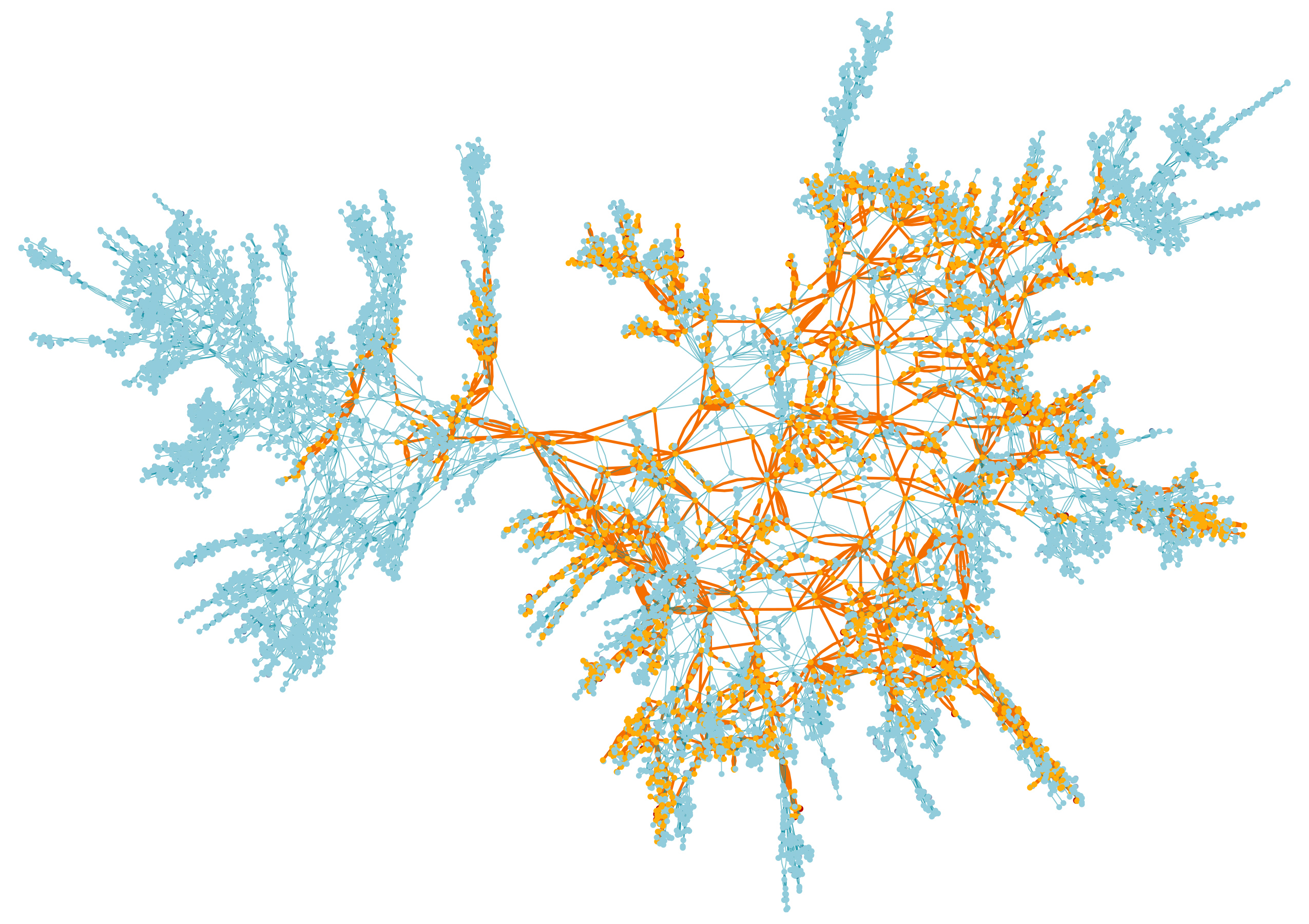 Map of peaks of a random surface, the largest cluster is marked in orange
Map of peaks of a random surface, the largest cluster is marked in orangeIn the second part, we study the very thing that happens there. Coloring the vertices in black and white with a fair coin, you get a good balance between clusters of black and white vertices. Clusters grow around each other, like weed thickets competing for a place in an overgrown garden, creating complex geometric shapes that don't appear when one of the flowers dominates among the peaks.
“By choosing a critical parameter, you discover large clusters,” said Sheffield. “However, they do not stain the whole thing, and they are not small.”
Since the surface was created at random, and the process of coloring the vertices is also random, a large cluster on one surface will always be different from a large cluster on another. But mathematicians have proved that for all surfaces and all possible ways to color their vertices, the largest clusters will have the same properties. The first thing they proved is the exact probability distribution of the sizes of the largest black clusters over all surfaces. They found that most often a cluster of a certain intermediate size occurs, and that the frequency with which larger or smaller clusters appear increases exponentially with distance from this intermediate.
They also argue that all large clusters can be reduced to a single canonical form, known as a “stable map”. The stable map refers to these clusters in the same way as the Brownian motion to random walk. This means that if individual clusters are slightly estranged - so that each random step inside the cluster is less noticeable in the geometry of the whole figure as a whole - then the clusters will gradually come to a common shape. They look like snowflakes: they seem unique near, but from a distance their commonality is clearly visible.
“They found this stable map, the natural limit of scaling,” Sheffield said.
The work expands the limits of knowledge concerning random forms and processes accumulated by mathematicians in recent years. It also reveals to us that it is precisely at that moment when the random system seems most chaotic that an exceptional geometric order begins to be seen through it.