There are two men named "Van Eck". The first, in 1985, showed the whole world how to intercept data from a monitor (
Van Eck phreaking ) for $ 15; the second, in 2010, came up with a cunning sequence (
Van Eck's sequence ). Steeper than the simplicity of the task of this sequence can only be its properties and puzzles.
So, the algorithm for generating sequence members. We take the "starting number", for example, "0", write out. The next term is how many steps back this number occurred in the previous sub-sequence. If never, then write zero. The next is how many steps back there was zero in the previous sub-sequence, that is, one step back. We write down the unit. Unit one - write zero. Oops, zero met two steps back. We are writing two, and so on ...
For the report point “0”, the first 97 members of the sequence:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1
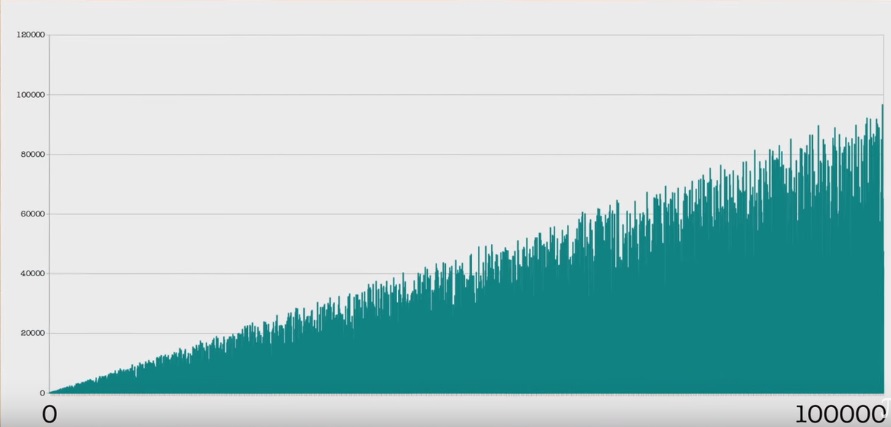
Schedule:
Even more timeline:
The properties of a sequence are quite easily proved that its maximum term increases all the time and that it has an infinite number of zeros. Or that there are no periods in it. (A few theorems and consequences
here .)
Logarithmic graph:
Program in Python:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
For the starting number "1", the first hundred is:
1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15
Schedule:
For the starting number "2", the first hundred is:
2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4
Schedule:
Sources