Key points or what this article is about
We continue the series of articles on
ShIoTiny - a visually programmable controller based on the
ESP8266 chip.
This article describes an example of a ventilation control project in a bathroom or other room with high humidity about how to build a program for
ShIoTiny .
Previous articles in the series.
ShIoTiny: small automation, the Internet of things, or “six months before the holidays”ShIoTiny: nodes, links and events or features of drawing programsReferences
Binary firmware, controller circuitry and documentationInstructions and description of nodesConfiguring MQTT broker cloudmqtt.comMQTT dashboard control panel for AndroidIntroduction
There is no understanding outside of experience. This is the truth tested by time and generations. Therefore, there is nothing better for learning practical skills than trying to do something on your own. And examples that show what can be done and what is not worth trying, here will come in handy. Other people's mistakes, of course, cannot prevent the occurrence of errors of their own, but can help reduce the number of the latter.
Questions and letters from readers of previous articles prompted me to make a small project, an example of ventilation control, in order to show how the ShIoTiny nodes work.
The initial idea, on the basis of which the
ShIoTiny controller
appeared - a
pumping and irrigation station - is far from suitable for everyone and will be interesting. Therefore, I took for everyone an understandable and many useful ventilation control system as an example.
I
’ll say that the idea of the project is not mine, but
I got it from here and then adapted it to
ShIoTiny .
First understand what you want
The cultivation process is endless. And it was this property that ruined many good ideas and projects. The developer, instead of releasing, if not an ideal, but a working thing, continued to improve it. And he perfected it until his competitors circumvented it, releasing, if not an ideal (and often frankly miserable), but working solution.
Therefore, it is very important to know where to put an end to the project. Or, in other words, it is necessary to determine what we want to get at the end of the project from what we have at the beginning. In Russian, for a document that is drawn up just to describe the way to create something, there is a beautiful short and capacious word “plan”, which mentally retarded translators and defective managers have recently begun to call the “road map” for some reason. Well, God bless them.
Our plan will be like that. Suppose there is a room in which the humidity can sometimes increase dramatically. For example, such as a bathroom or kitchen. Humidity is an unpleasant thing and the way to deal with it is as old as the world: ventilate the room. There are quite a few airing methods. But we, perhaps, will refuse exotic and old-fashioned ways like Negroes with webs and stop at the usual fan. Fans are cheaper, and finding them in our area is easier.
In short, we want to control the fan: turn it on and off, respectively. More precisely, we want it to turn on and off when necessary.
It remains to determine: under what conditions should the fan turn on and under what conditions - turn off.
Everything is obvious here: if the humidity is above a predetermined limit, the fan turns on and draws air; humidity has returned to normal - the fan turns off.
The attentive reader will immediately catch his eye on the word "given." Who is given? How preset?
There are several ways to set threshold humidity. We will consider two of them: the first - using variable resistance and the second - over the network via the MQTT protocol. Each of these methods has advantages and disadvantages, which will be discussed later.
For those who don’t understand, I’ll explain that the “threshold humidity” is such a humidity level, exceeding which requires turning on the fan.
The next question is whether to give the user the right to turn on the fan directly? That is, regardless of the humidity level, at the touch of a button? We will provide such an opportunity. After all, a fan may be needed not only with high humidity, but also to remove from the room, for example, an unpleasant odor, popularly referred to as “stink”.
So, we understood what we want and even a little how it will work. We list briefly all the functions of our ventilation control system:
- setting a threshold humidity level (two options);
- humidity measurement;
- automatic inclusion of the fan;
- automatic shutdown of the fan;
- manual inclusion of the fan (at the touch of a button).
So, the plan is clear. It is necessary to implement all of the above functions in our program. On the basis of this “plan” we will act. To begin, let's draw a block diagram of the device.
Device block diagram
Generally speaking, we will have two such schemes. The first is for the option in which the threshold moisture level is set by a variable resistance. The second scheme is for the option in which the threshold humidity level is set via the network via the MQTT protocol.
But since these schemes will differ by only one element - the variable resistor "setting the threshold humidity level", then we will draw only one structural scheme. Of course, the structural scheme according to GOST looks different. But we focus not on bison engineers, but on the younger generation. Therefore, visibility is more important.
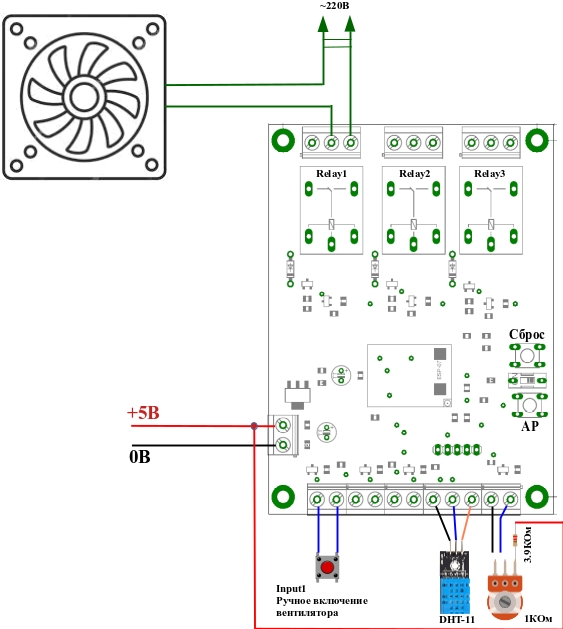
So, what do we see in the picture? The fan is connected to the
Relay1 relay of the
ShIoTiny controller. I draw your attention to the fact that the fan is a contraption that lives under high voltage. Therefore, if anyone will do this himself - be careful. That is, at least, before sticking your fingers or measuring instruments into the circuit - disconnect at least the fan. And the second point. If your fan is more powerful than
250W , then you
should not connect it directly to
ShIoTiny - only through the starter.
We figured out the fan. Now the “manual on” button of the fan. It is connected to input
Input1 . There is nothing more to explain.
Temperature and humidity sensor
DHT-11 (or
DHT-22 or their analogues). To connect it, a special input is provided on the
ShIoTiny controller. As you can see in the figure, connecting such a sensor also does not present problems.
And finally, a variable resistance that sets the threshold humidity level. More precisely, a divider consisting of variable and constant resistances. There are no problems with its connection, but I will explain that the built-in ADC on the
ESP8266 is designed for a maximum of 1 volt. Therefore, a voltage divider is needed about 5 times.
And once again I remind you that this divider is not needed if the threshold humidity level is set via the network using the MQTT protocol.
We will begin to draw up the algorithm of the device in the ElDraw ShIoTiny editor. How to get there, in this editor, you can read in the articles earlier or in the instructions, a link to which is at the beginning of the article.
Option one, the simplest
Let's start with a simple one: turn on the
Relay1 relay
when the threshold humidity level is exceeded for a given time.
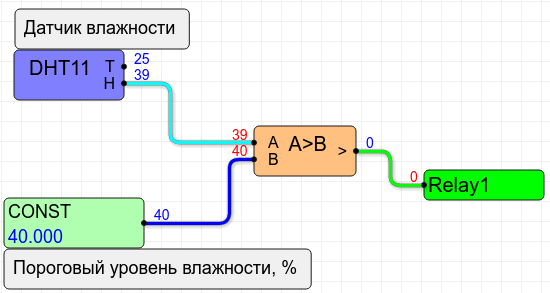
As you can see, nothing complicated: there are only four nodes, not counting the comment nodes.
DHT11 is actually a temperature and humidity sensor (can be changed to
DHT22 ).
CONST constant - threshold moisture level, in percent.
Comparator - a node comparing two numbers and setting output 1 if the specified condition is met and 0 if the condition is not met.
In our case, this condition will be
A> B , where
A is the humidity level measured by the sensor, and
B is the threshold level of the same humidity.
As soon as the measured humidity level (
A ) exceeds the threshold humidity level (
B ), 1 will immediately appear at the output of the comparator
A> B and the relay will turn on. Conversely, as soon as the humidity level returns to normal (that is,
A <= B ), immediately at the output of the comparator
A> B, 0 will appear and the relay will turn off.
All clear? To whom it is not so - read again or look at the description of the operation of the nodes in the instructions.
I note that the data from the
DHT11 sensor
is updated approximately once every 10 seconds. Therefore, the relay will not be able to turn on and off more often than once every 10 seconds.
Everything would be fine, but we would like to set the threshold humidity level using a variable resistor. Nothing is easier!
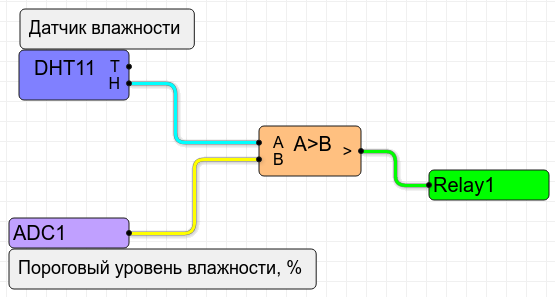
Just replace the constant node with the ADC node. After all, we connected the voltage divider with a variable resistor to the ADC.
The voltage at the input of the ADC varies from 0 to 1 Volt. But the humidity at the output of the sensor - varies from 0 to 100%. How do we compare them? Everything is simple. The ADC unit in
ShIoTiny not only measures the input voltage, but also knows how to
scale and shift it .
That is, at the output of the ADC1 node (ADC) will be the value of
X calculated by the formula
where
- voltage at the ADC input (from 0 to 1V);
k - range (ADC range) and
b- offset (ADC offset). Thus, if you set
k = 100 and
b = 0 , then when changing
in the range from 0 to 1, the value of
X at the output of the ADC unit will vary in the range from 0 to 100. That is, numerically equal to the range of humidity changes from 0 to 100%.
Or, simply, by turning the variable resistance engine, you can set the threshold humidity level from 0 to 100. The only inconvenience is that there are no display devices. But in practice, if the engine of variable resistance makes 6 divisions 0%, 20%, 40%, 60%, 80%, 100%), then this is enough to set the threshold humidity level.
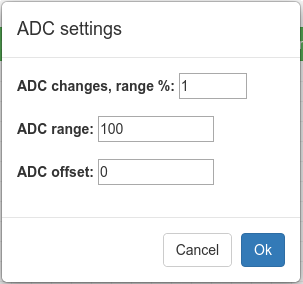
How do we set the coefficients
k - range (ADC range) and
b- offset (ADC offset)? Yes, it’s easier than steamed turnips! Click with the mouse pointer in the
ADC1 node and immediately you will see the settings window. In it, you can set everything you need. For our case, it will be such a window, as in the figure.
So, we have the simplest working solution. Let's start to improve it.
By the way, the simplest solution has one advantage - it does not need the Internet. It is completely autonomous.
Option two, connect the button
Everything works and everyone is happy. But bad luck, we can’t turn on the ventilation forcefully. We have already agreed that a button will be connected to the input
Input1 , which will turn the fan on and off forcibly, not paying attention to the humidity sensor.
It's time to process this button in our circuit program.

The button click processing unit is highlighted in orange. It is a button click counter that is reset to zero when the value at its output exceeds one (green line,
CT node output).
Everything works here as plainly as before: the
CT counter counts the clicks of the button connected to
Input1 . That is, the value at the output of this counter increases by 1 with each click of the button.
As soon as this value becomes equal to two (that is, more than 1), immediately on the output of the comparator
A> B appears 1. And this 1 will reset the counter
CT to zero. This means the comparator, the lower one according to the scheme!
Thus, our button has two states - 0 and 1. If we needed more states (3 or 4 or even more) - it would be enough for us to change the
CONST constant from one to another value.
So, we have two conditions for turning on the fan: exceeding the set humidity level and pressing the button once. If any of the conditions is met, the fan will turn on. And it will work until the button is pressed again
AND the humidity level returns to normal.
You can, of course, complicate the algorithm even more, but we will not do this - we will leave room for creativity for those who wish.
Option Three, connect to the Internet
Everything that we described is quite functional. But what about the show off? After all, any pimpled hipster-hacker-cracker will laugh at someone who twists a pen and presses a button, and does not control it from a smartphone! To twist the handle is “not fashionable”. But to crawl your finger on the smartphone, erasing this finger into the blood - here it is, the peak of desires of the hipster-hacker-cracker (I could never distinguish all of them - so if I made a mistake, I'm sorry).
But we will be condescending to these individuals. Internet governance has real advantages. First of all, it’s visual. There are lots of applications for all platforms that allow a couple of pokes to create a completely usable control panel for our Carlson controller. Secondly, it is an opportunity to remotely monitor the state of humidity in the room. And thirdly, you can see not only what the fan does - spinning or not, but also what threshold humidity level is set. And then - the fan turned on automatically or manually. In general, whatever you want.
Of course, for some fan there is a lot of honor - so much attention. But this is just an example.
So, for connecting to the Internet we will use the
MQTT technology and the protocol of the same name.
To use this technology, we need an
MQTT broker . This is such a special server that serves
MQTT clients , for example,
ShIoTIny and your smartphone.
The essence of
MQTT technology is that any client publishes arbitrary data under a specific name (called
topic in
MQTT terminology) on an MQTT broker (server). Other customers can subscribe to arbitrary data by their name (
topic ) and receive newly published data. That is, the entire data exchange is on the principle of client-broker-client.
I
will not focus on the details. There are tons of articles and tutorials on the Internet on how
MQTT works and what kind of programs there are for creating control panels. I’ll just show you how to receive and publish data using
ShIoTiny .
As a broker, I used
www.cloudmqtt.com , but the principle is the same everywhere.
So, we will assume that you have registered with the
MQTT broker . In general, the broker will give you (or require to invent) a username and password (for authorization), as well as a port for connection.
There are two ways to connect
ShIoTiny to the
MQTT broker - regular connection and
TLS (
SSL ).
All these parameters in
ShIoTiny are entered on the
Networking tab, the
MQTT Connection to server section.
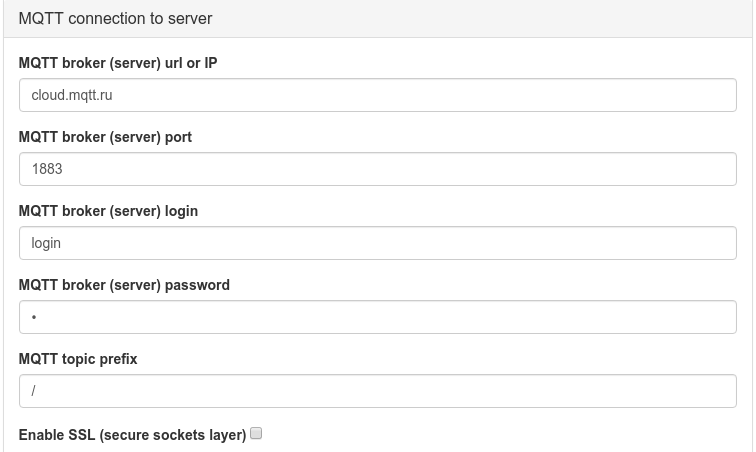
If your
MQTT broker does not require authorization, do not enter your login and password (leave these fields empty).
The
MQTT topic prefix parameter requires a separate explanation.
The prefix of MQTT parameters is a line added to the topic title when publishing and subscribing to the MQTT broker. To set the
MQTT prefix for your controller, you just need to enter it in the input field "
MQTT topic prefix " ("
MQTT topic prefix "). The prefix always begins with a slash (
"/" )! If you do not enter a slash in the input field, it will be added automatically. The
“#" and
"+" characters cannot be used in the prefix. There are no other restrictions.
For example, if you publish the parameter “
status ” (or subscribe to it), and your prefix is set to “
/ shiotiny / ”, then on the broker this parameter will be published under the name “
/ shiotiny / status ”. If you have an empty prefix set, then all parameters on the broker will begin with a slash (
“/” ): “
status ” will be published as “
/ status ”.
So, we believe that you have registered with the
MQTT broker and received your login, password and port. Then you set these parameters on the
Networking tab, the
MQTT Connection to server section of the ShIoTiny controller.
We believe that the prefix is set to "
/ room / ".
To begin with, we
’ll publish the status of all key parameters:
Realay1 relay, manual on state, automatic on state and, finally, threshold and current humidity levels. Well and a bonus - the temperature in the room. How to do this, see the figure.
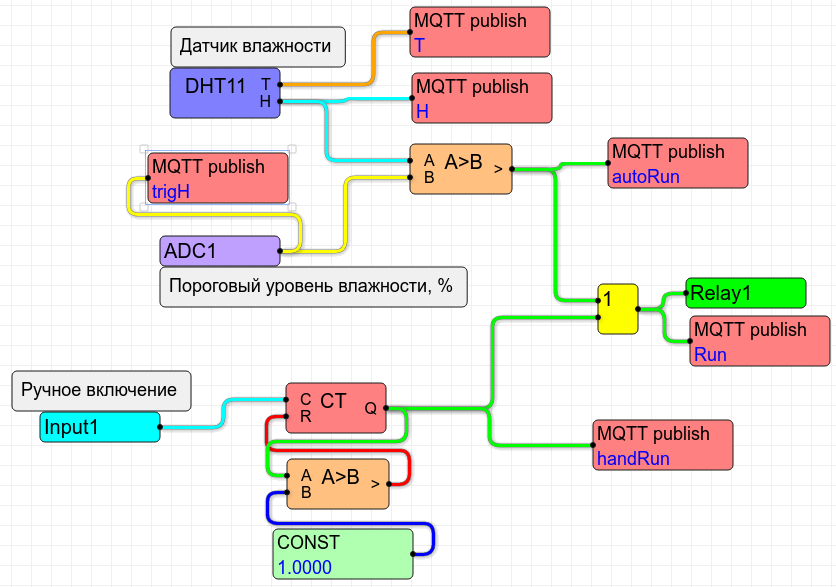
As you can see, the difference from the previous version is only the
MQTT Publish nodes. Given the prefix, the following parameters are published:

As you can see, the entire state of the system is in full view!
But we want to not only see, but also control. How to be Very simple. We will refuse to set the threshold humidity level using the
ADC and a variable resistor and will set this same threshold humidity level by
MQTT directly from the smartphone!
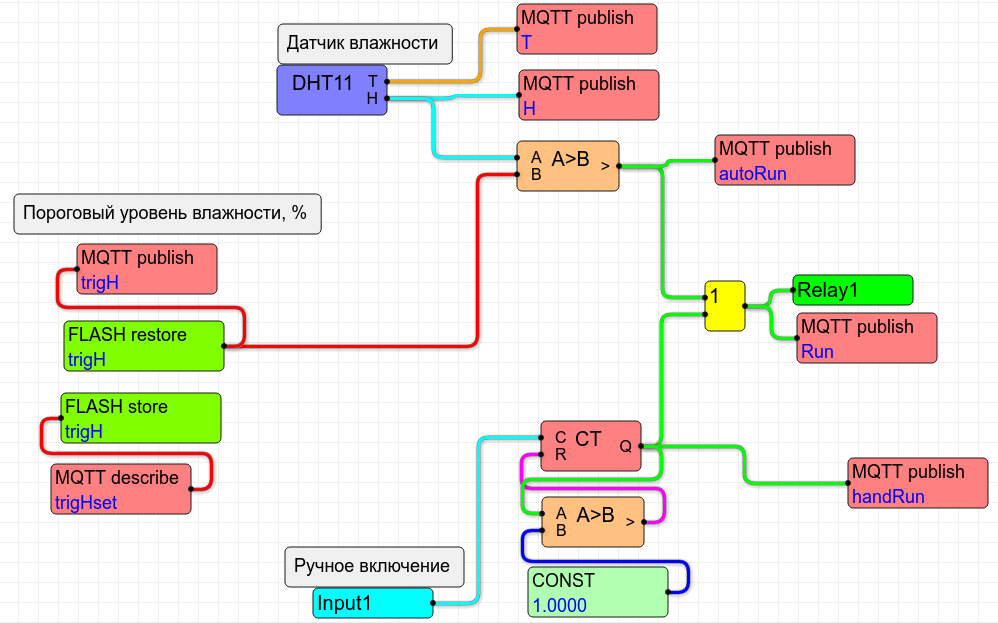
We remove the ADC node from the circuit and include three new nodes there:
FLASH store ,
FLASH restore and
MQTT describe .
The function of the
MQTT describe node is obvious: it receives the parameter
/ room / trigHset (threshold humidity level) from the
MQTT broker . But what does he do with the data next? It simply gives them to the
FLASH store node, which, in turn, stores this data in non-volatile memory under the name
trigH . After that, the
FLASH restore node reads data from the non-volatile memory under the name
trigH, and what happens next we already know.
Why such difficulties? Why can not I immediately send the received data to the input of the comparator?
As Comrade S. Holmes used to say,
this is elementary ! No one guarantees that after turning on your device, it will join the
MQTT broker . And humidity must be measured. And the fan must be turned on. But without information on the threshold humidity level, this is impossible! Therefore, when turned on, our device extracts a previously stored threshold moisture level from non-volatile memory and uses it for decision-making. And when the connection with the
MQTT broker is established and someone publishes a new value
/ room / trigHset , then this new value will be used.
Then you can invent anything you want. For example, in addition to humidity, also enter a temperature record. Or add a “smart” lighting control (we still left unused two relays and two inputs). All in your hands!
Conclusion
So we looked at several examples of the implementation of the simplest in essence controller based on ShIoTiny. Maybe it will be useful to someone.
As always, suggestions, wishes, questions, typos, etc., by e-mail:
shiotiny@yandex.ru