 Source: xkcd
Source: xkcdLinear regression is one of the basic algorithms for many areas related to data analysis. The reason for this is obvious. This is a very simple and understandable algorithm, which has contributed to its widespread use for many tens, if not hundreds, of years. The idea is that we assume a linear dependence of one variable on a set of other variables, and then try to restore this dependence.
But in this article we will not talk about the use of linear regression for solving practical problems. Here we will consider interesting features of the implementation of distributed recovery algorithms that we encountered when writing a machine learning module in
Apache Ignite . A little basic math, the basics of machine learning, and distributed computing will help you figure out how to restore linear regression, even if the data is distributed across thousands of nodes.
What are we talking about?
We are faced with the task of restoring linear dependence. As input, a set of vectors of supposedly independent variables is given, each of which is associated with a certain value of the dependent variable. These data can be represented in the form of two matrices:
\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}
Now, since the dependence is assumed, and besides it is linear, we write our assumption in the form of a product of matrices (to simplify the notation here and below, it is assumed that the free term of the equation is hidden behind
, and the last column of the matrix
contains units):
\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}
Very similar to a system of linear equations, right? It seems, but most likely there will be no solutions to such a system of equations. The reason for this is the noise that is present in almost any real data. Also, the reason may be the lack of a linear relationship as such, which you can try to fight by introducing additional variables that nonlinearly depend on the source. Consider the following example:
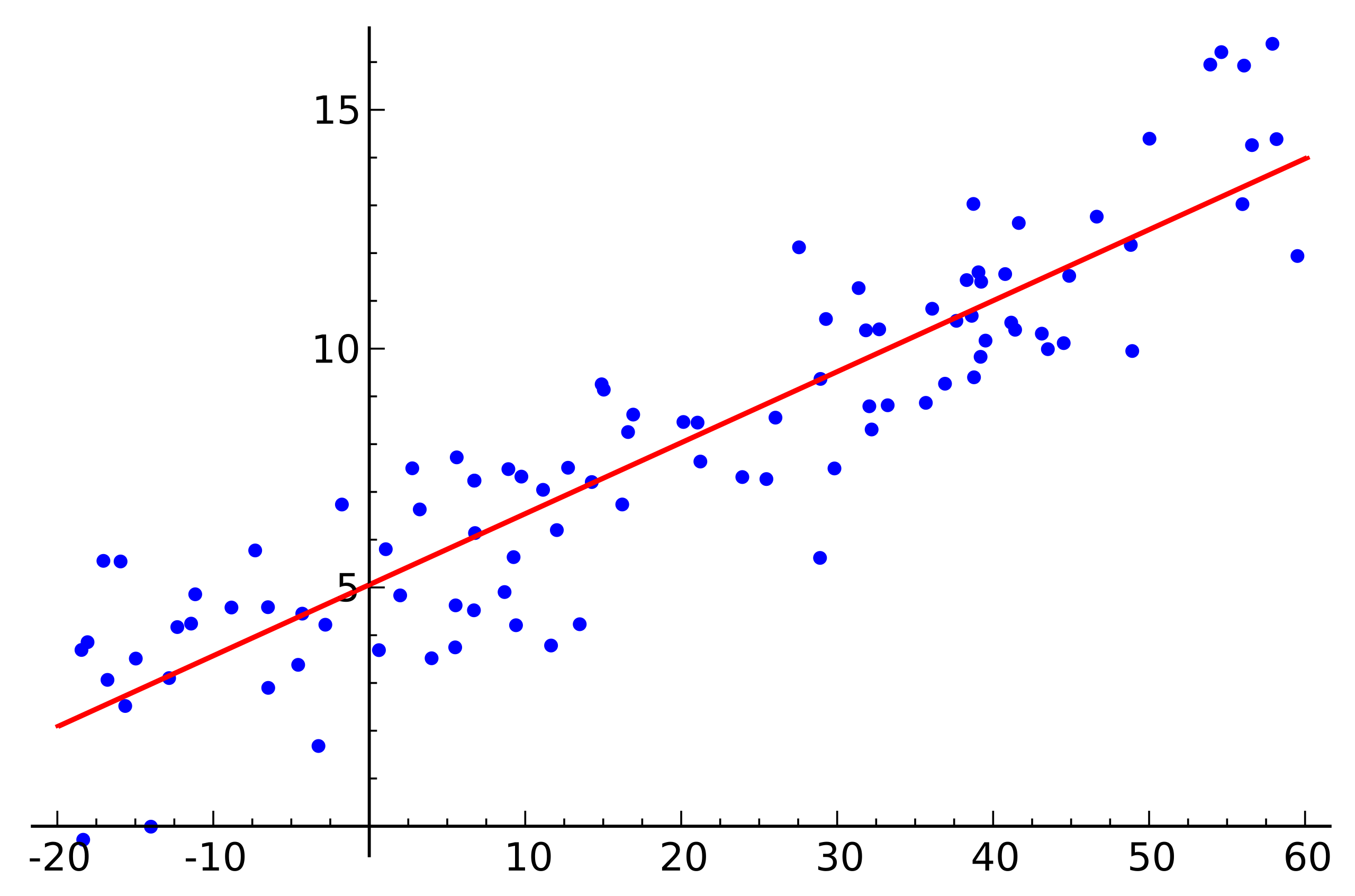 Source: Wikipedia
Source: WikipediaThis is a simple linear regression example that shows the dependence of one variable (along the axis
) from another variable (along the axis
) For the system of linear equations corresponding to this example to have a solution, all points must lie exactly on one straight line. But this is not so. But they do not lie on one straight line precisely because of noise (or because the assumption of the presence of a linear dependence was erroneous). Thus, in order to restore a linear dependence from real data, it is usually necessary to introduce one more assumption: the input data contains noise and this noise has a
normal distribution . One can make assumptions about other types of noise distribution, but in the vast majority of cases it is the normal distribution that will be discussed later.
Maximum likelihood method
So, we assumed random randomly distributed noise. How to be in such a situation? For this case, in mathematics there exists and is widely used
the maximum likelihood method . In short, its essence lies in the choice of
the likelihood function and its subsequent maximization.
We return to the restoration of linear dependence from data with normal noise. Note that the assumed linear relationship is a mathematical expectation
available normal distribution. At the same time, the probability that
assumes one or another value, subject to the presence of observables
, as follows:
We substitute now instead
and
the variables we need are:
It remains only to find the vector
at which this probability is maximum. To maximize such a function, it is convenient to prologarithm first (the logarithm of the function will reach its maximum at the same point as the function itself):
Which, in turn, boils down to minimizing the following function:
By the way, this is called the
least squares method. Often, all the above reasoning is omitted and this method is simply used.
QR decomposition
The minimum of the above function can be found if you find the point at which the gradient of this function is equal to zero. And the gradient will be written as follows:
QR decomposition is a matrix method for solving the minimization problem used in the least squares method. In this regard, we rewrite the equation in matrix form:
So, we lay out the matrix
on matrices
and
and perform a series of transformations (the QR decomposition algorithm itself will not be considered here, only its use in relation to the task):
\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}
Matrix
is orthogonal. This allows us to get rid of the work.
:
\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}
And if you replace
on
it will turn out
. Given that
is the upper triangular matrix, it looks like this:
\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}
This can be solved by the substitution method. Element
is like
previous item
is like
and so on.
It is worth noting here that the complexity of the resulting algorithm through the use of QR decomposition is
. Moreover, despite the fact that the matrix multiplication operation is well parallelized, it is not possible to write an effective distributed version of this algorithm.
Gradient descent
Speaking about minimizing a certain function, it is always worth recalling the method of (stochastic) gradient descent. This is a simple and effective minimization method based on iteratively calculating the gradient of the function at a point and then shifting it to the side opposite to the gradient. Each such step brings the solution to a minimum. The gradient looks the same:
This method is also well parallelized and distributed due to the linear properties of the gradient operator. Note that in the above formula, independent terms are under the sum sign. In other words, we can calculate the gradient independently for all indices
from first to
, in parallel with this, calculate the gradient for indices with
before
. Then add the resulting gradients. The result of the addition will be the same as if we immediately calculated the gradient for the indices from the first to
. Thus, if the data is distributed between several parts of the data, the gradient can be calculated independently on each part, and then the results of these calculations can be summed to obtain the final result:
In terms of implementation, this fits into the
MapReduce paradigm. At each step of the gradient descent, a task for calculating the gradient is sent to each data node, then the calculated gradients are collected together, and the result of their summation is used to improve the result.
Despite the simplicity of implementation and the ability to execute in the MapReduce paradigm, gradient descent also has its drawbacks. In particular, the number of steps required to achieve convergence is significantly larger in comparison with other more specialized methods.
LSQR
LSQR is another method of solving the problem, which is suitable both for reconstructing linear regression and for solving systems of linear equations. Its main feature is that it combines the advantages of matrix methods and an iterative approach. Implementations of this method can be found both in the
SciPy library and in
MATLAB . This method will not be described here (it can be found in the
LSQR article
: An algorithm for sparse linear equations and sparse least squares ). Instead, an approach will be demonstrated to adapt the LSQR to execution in a distributed environment.
The LSQR method is based on the bidiagonalization
procedure . This is an iterative procedure, each iteration of which consists of the following steps:

But based on the fact that the matrix
horizontally partitioned, then each iteration can be represented as two steps MapReduce. Thus, it is possible to minimize the data transfers during each iteration (only vectors of length equal to the number of unknowns):
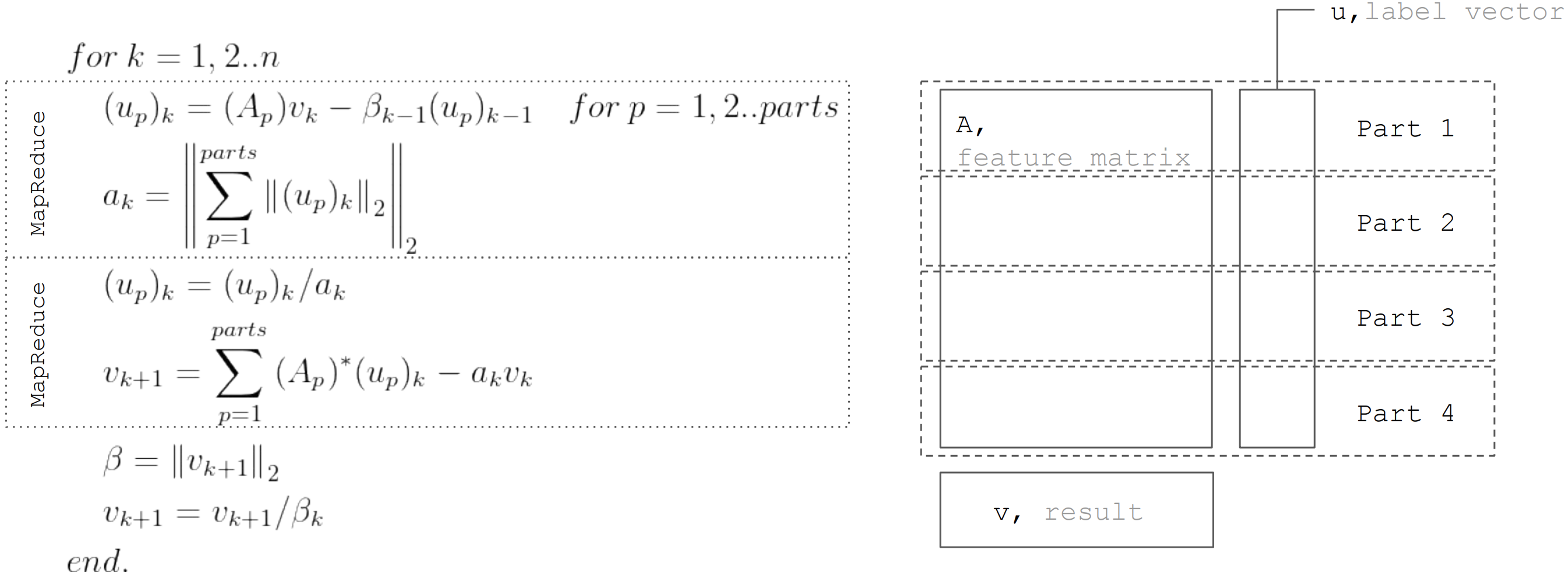
This approach is used when implementing linear regression in
Apache Ignite ML .
Conclusion
There are many linear regression recovery algorithms, but not all of them can be applied in any conditions. So QR decomposition is great for accurate solution on small data arrays. Gradient descent is simply implemented and allows you to quickly find an approximate solution. And LSQR combines the best properties of the previous two algorithms, since it can be distributed, converges faster in comparison with gradient descent, and also allows an early stop of the algorithm, unlike QR decomposition, to find an approximate solution.