Hello, Habr!
In coloring, there are several methods for constructing a color gamut (color palette), based on the arrangement of colors relative to each other in the color wheel and, as a rule, having the same brightness. The harmonious perception of which is not sufficiently substantiated from a physical point of view.
In the theory of music there is the concept of consonant intervals. Consonances are called intervals that sound more soft and harmonious. There are three groups of consonances: very perfect (pure unison, octave), perfect (pure fifth, pure fourth) and imperfect (large third, small third, sixth). There is also the concept of a consonant chord - a major or minor triad, consisting solely of consonant intervals.
Acoustically, the essence of the difference between consonance and dissonance is expressed in different lengths of periods of regularly repeated oscillation groups. The criterion for the difference between consonance and dissonance is the simplicity or complexity of the relationship: the simpler the relationship, the more consonant, the more complex the more dissonant, where numerical proportions can be expressed in two ways: through ratios of string lengths or through ratios of the number of oscillations. In other words, the degree of consonance of two notes is determined by the number of coincidence periods of the corresponding harmonic functions of the dependence of sound pressure on time per unit time.

Fig. 1: Graph of sound pressure versus time at a fixed distance from the sound source.
For example, notes to and salt (pure fifth) have sound wavelengths that differ by one and a half times. The graphs of the functions of the dependence of the sound pressure of notes on time intersect on the abscissa axis (sound pressure equal to zero) when the sound pressure function of the note before makes two oscillations, and the salt function of the note makes three (Fig. 1). In Figure 1, this moment is marked with a vertical line.
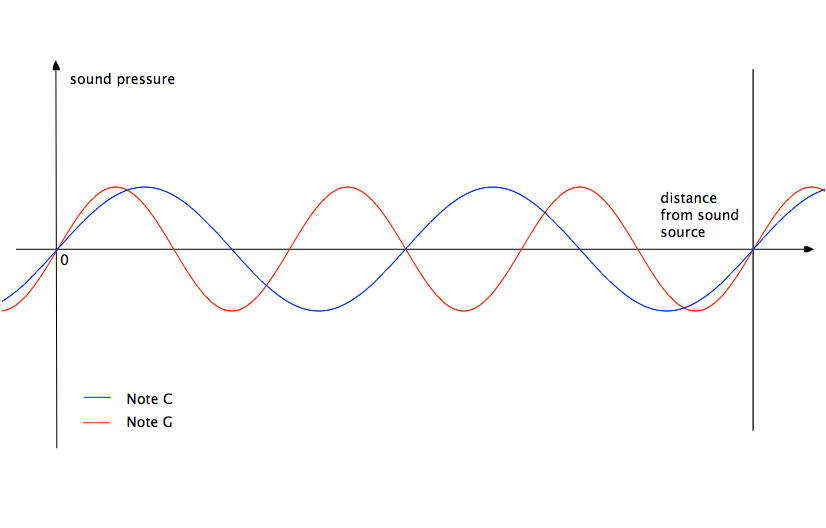
Fig. 2: Graph of sound pressure versus distance from a source at a fixed point in time.
If we imagine the propagation of sound pressure in space at a fixed point in time (near the sound source), then we get the same picture (Fig. 2).
The notes before and mi (major third) have sound wavelengths differing 5/4 times. Their graphs intersect on the abscissa axis when the sound pressure function of the note to makes 4 vibrations, and the function of the note mi is 5. It is precisely because of this that the pure fifth is more consistent than the big third.
Color, like sound, is also a wave (particle-wave dualism). In the case of constructing a consonant interval for color, we are not limited to a small set of notes, but are limited by the boundaries of the wavelengths of visible light, just like sound is limited by the boundaries of the wavelengths of the audible sound. The absence of restrictions on a small set of notes leads to the fact that we can significantly expand the list of intervals - 3/2; 3/4; 2/5, 3/5, 4/5, ...
Wave method of constructing a color scheme
Consider the construction of colors for spectral and non-spectral colors.
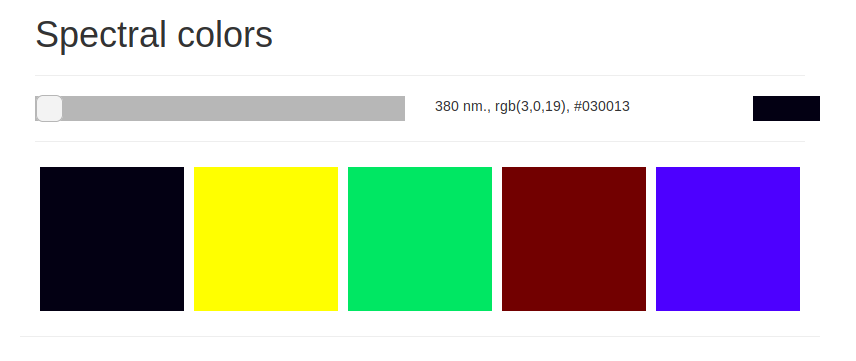
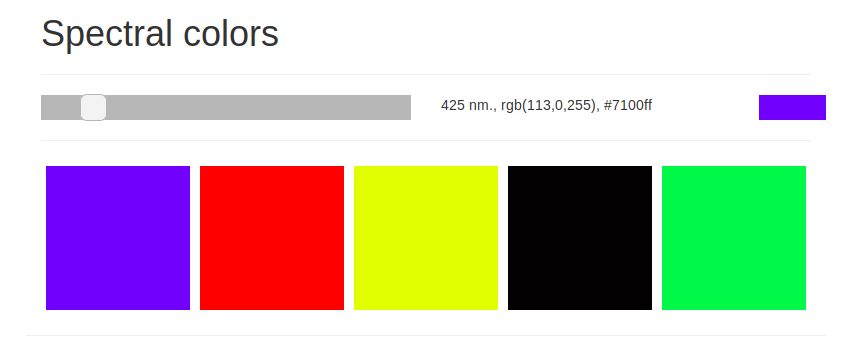
A spectral color is a color having a specific wavelength. To build a color palette, we take, first, the most consonant color to it - this is a color with a wavelength that differs by 1.5 times, but does not go beyond the visible spectrum. Further, in a similar way, we will take less consonant intervals until we reach the desired number of colors in the desired palette.

Fig. 3: Graph of electric field strength versus distance from the source at a fixed point in time.
Take, for example, blue with a wavelength of 450 nm. A color whose wavelength is less than 1.5 times goes beyond visible radiation. A color with a wavelength greater than 1.5 times (675 nm.) Is red. A color with a wavelength greater than 3/4 times (600 nm.) Is an orange color. As a result, we got the following color scheme: the main color is blue, the most suitable color is red, and the orange color is slightly less suitable for blue (Fig. 3). The same results can be achieved by operating instead of wavelengths with their frequencies.
Also in music there is the concept of fret. The combination of notes can sound not only harmonious, but also have a shade - fret (Ionian, Dorian, Phrygian, Lydian, ...). Similar feelings can be transferred to the color scheme, using the appropriate proportions when building it.
Non-spectral colors include colors that are not contained in the spectrum and consist of several spectral colors. Based on Grassmann's law of additivity, it follows that in the case of selecting a color gamut for non-spectral colors, the same operations should be performed on its constituent colors while maintaining proportions and taking into account the boundaries of the wavelengths of the visible spectrum.
Let us consider in more detail the phenomenon of consonance between two non-spectral colors. A musical sound consists of elementary tones since, together with the oscillation of the sound source itself as a whole, its parts also oscillate. The vibrations of the parts of the vibrating body give rise to weak sounds - overtones absorbed by the fundamental tone. The complex tone-forming scale of simple tones of the corresponding amplitudes is called the frequency spectrum. All elementary tones included in a complex sound are called harmonics. The degree of consonance of the interval is determined by the number of coinciding harmonics of the spectra of both notes: the more harmonics coincide, the more consonant the interval.

Fig. 4: Graph of sound pressure versus time at a fixed distance from the sound source.
Based on this, we believe that the essence of the phenomenon of harmony (consonance) consists in the simultaneous state of rest (energy is zero) of both waves. In the graphs, this resting state is displayed at the intersection of two wave functions on the abscissa (time) axis (Fig. 4). And the degree of consonance of two wave functions is determined by the number of such intersections per unit of time (or length, subject to the same propagation velocity): the more, the more consonant. This concept of degree of consonance also extends to non-spectral colors, since they are also wave functions.
Implementation of the wave method on the example of white in the sRGB system
A person is able to perceive colors with wavelengths in the range of 380 - 780 nm. Any four colors are linearly dependent, but there are an infinite number of combinations of three colors that are linearly independent (Grassmann's first law). Grassman's independence of colors is that the color sensation caused by one of the three colors cannot be obtained by mixing the other two colors in any proportions. It was noticed that it is most convenient to operate with red, green and blue colors. It is by this principle that almost all modern monitors work.
In 1931, the International Lighting Congress (CIE) adopted a characterization of the color properties of the average (standard) observer, based on the results obtained in 1926 - 1930. Wright and Guild. The basis of this colorimetric standard, which is valid to this day, is the following colors: 700 nm. (red), 546.1 nm (green) and 435.8 nm. (blue) (RGB system). The adopted characteristic contains the relationship between the resulting wavelength of the mixture and the amount of red, green and blue colors in this mixture.
Further, for convenience of calculations, the International Lighting Congress introduced the abstract system CIE XYZ, based on unrealistic colors. This coordinate system is very convenient for the transition from one system to another. The wavelengths of visible light and the corresponding coordinates of the CIE XYZ mixture were also calculated based on the results obtained for the RGB system.
To reproduce the same color sensations on different output devices (monitor or printer), each such device has its own color profile, which contains its connection with the abstract CIE XYZ system. In other words, the color profile serves to enable the transition between different color systems (sRGB, AdobeRGB, ...). The most common color space is the sRGB system. Next, we consider the implementation of the wave method specifically for this system.
We find the wavelengths of red, green and blue in the sRGB system. To do this, we use the transition formulas from the sRGB system to CIE XYZ (with a white point D65). As a result, for red rgb (255, 0, 0) , green rgb (0, 255, 0) and blue rgb (0, 0, 255) we obtain the following coordinates in the CIE XYZ system: red - (0.412456, 0.212673, 0.019334), green - (0.357576, 0.715152, 0.119192), blue - (0.180437, 0.072175, 0.950304).
Using tables containing the wavelengths of visible light (CIE 1931 2-deg, XYZ CMFs) and the corresponding coordinates of the CIE XYZ mixture, we find the wavelengths for red, green and blue in the sRGB system: red - 611.4 nm., Green - 549.1 nm., blue - 464.2 nm.
Now we find the “pure fifth” for this color - a color with a wavelength greater than 1.5 times:
for red - 611.4 nm. x 1.5 = 917.1 nm. (goes beyond the visible spectrum, black color),
for green - 549.1 nm. x 1.5 = 823.65 nm. (almost black color),
for blue - 464.2 nm. x 1.5 = 696.3 nm. (Red color).
Next, using the same tables, we find the coordinates for the waves obtained in the CIE XYZ system:
for red - 917.1 nm. - (0, 0, 0),
for green - 823.65 nm. - (0.000001905497, 0.000000688110, 0.000000000000),
for blue - 696.3 nm. - (0.014790640000, 0.005343059000, 0.000000000000).
Then we transfer each of the received colors back to the sRGB system:
for red - 917.1 nm. - rgb (0, 0, 0),
for green - 823.65 nm. - rgb (0.0168, -0.0018, 0.0000),
for blue - 696.3 nm. - rgb (56.1246, -13.7888, -0.8801).
Rounding to the nearest integer and discarding what is less than zero, we get:
for red - 917.1 nm. - rgb (0, 0, 0),
for green - 823.65 nm. - rgb (0, 0, 0),
for blue - 696.3 nm. - rgb (56, 0, 0).

Fig. 5: RGB color image (56, 0, 0).
Summing up the three resulting colors, we end up with a dark red color which in the spectrum is close to infrared - rgb (56, 0, 0) (Fig. 5).
The implementation of the algorithm was shown above using the white rgb (255, 255, 255) times 3/2 as an example. Here, the relative brightness was not taken into account, for the calculation of which it is also necessary to convert to the xyY system.
Implementation of the wave method in computer graphics
Along with the sRGB and CIE XYZ systems, there is also the xyY system, where the x and y components are responsible for the wavelength, and the Y component for the relative color brightness. We perform the transformation from the previous paragraph with arbitrary colors rgb (r, g, b). To do this, we first find the coordinates of the maximum red, green and blue colors in the xyY system:
rgb (255, 0, 0) - xyY (0.640000, 0.330000, 0.212673),
rgb (0, 255, 0) - xyY (0.300000, 0.600000, 0.715152),
rgb (0, 0, 255) - xyY (0.150000, 0.060000, 0.072175).
In this case, we are only interested in the brightness component Y:
rYmax = 0.212673,
gYmax = 0.715152,
bYmax = 0.072175.
Next, translate the blue color of rgb (0, 0, b) into the xyY system, through CIE XYZ, taking into account gamma correction:
rgb (0, 0, b) - xyY (bx, by, bY).
As a result, the brightness of the color that we obtained for blue in the previous paragraph should be less than bY / bYmax times. For rgb color (0, 0, 255), we obtained a color with a wavelength of 696.3 nm. which corresponds to the color in the xyY system with xyY coordinates (0.734621, 0.265379, 0.00543824). As a result, we get: xyY (0.734621, 0.265379, 0.00543824 * bY / bYmax). Next, we will convert to the sRGB system and get the color rgb (br, bg, bb).
Performing similar actions for the colors rgb (r, 0, 0) and rgb (0, g, 0), we obtain rgb (rr, rg, rb) and rgb (gr, gg, gb), respectively.
Next, we add these colors, taking into account the brightness. First, we sum rgb (rr, 0, 0), rgb (gr, 0, 0) and rgb (br, 0, 0). By converting each of these colors to the xyY system, we obtain the corresponding brightnesses - rrY, grY, brY. Find the total brightness of red: rY = rrY + grY + brY. The final color will have the following coordinates - xyY (0.640000, 0.330000, rY). When transferring sRGB to the system, we get rgb (rNew, 0, 0). Similarly, find gNew and bNew. The resulting color in the sRGB system will have the rgb coordinates (rNew, gNew, bNew).
PS
This article described and justified from a physical point of view the wave method we developed for constructing the color gamut. His understanding of the essence of the phenomenon of harmony was described. The article also described the algorithm for implementing the wave method for the sRGB color model in computer graphics.
This method can be widely used in various design industries. The results are on the website https://wavepalette.com/ru/ and will be regularly updated and, if necessary, adjusted. The corresponding article was published on arxiv.org .
PPS
On the site next to each color, the conversion and direction are indicated by a fraction and an arrow (3/2 ↑). Double conversion is indicated by two arrows (4/3 ↑↑ which is equivalent to 16/9 ↑). The first two colors will almost always be dark red and dark purple, as the 3/2 and 2/3 conversions are close to the infrared and ultraviolet color of the spectrum. At first I thought to exclude them from the palette, but then I decided to leave it anyway.
PPPS
The algorithm for constructing colors for any color in the sRGB system still requires refinement. In my opinion, good results that the algorithm can use are shown in spectral colors - https://wavepalette.com/en/spectral/ .