Just division, or how to create a mathematical theory and earn $ 400K on it. Series two, penultimate

In the previous series, we examined fractional numbers that did not include rational numbers. Today, we are waiting for exactly this, not considered part, and we will also prepare for a slightly more complicated final part without using terms like rings of residue classes or comparisons modulo with discrete logarithm. Also in the third part of those interested, prizes of $ 400K are waiting. Why in the third? Because without an introduction to the subject it is not always easy to understand the reasons why prizes are not so easy to get. And after reading - only luck and some purposeful, patient, but not very difficult, activity, that’s all you need.

Rational stars

To answer the previously asked questions about rational numbers, we again need a small digression. First, remember that in the process of dividing by the “corner” we constantly get the remainder from dividing a certain part of the divisible number by the divisor. In this case, the whole part of the division is written into the result, and the remainder of the division is multiplied by the base of the number system, after which the division procedure with the remainder is repeated until the period is detected or all the factors of the divisor are reduced and we get the final fraction.

It looks like this:

5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... 

Here, the remainder of subtracting 18 from 20 is always equal to two, which we then multiply by the base of the decimal number system.

Now let’s think how the division of 5 by 3 differs from, for example, the division of 1 by 3? The answer is simple - the presence of an integer part as a result. But we wondered about the period and the part that goes before the period (called - the pre-period), but is not included in the whole part of the result. Therefore, we do not need to consider the whole part. Therefore, in this example, all numbers greater than 3 or equal to it can be excluded from consideration. And what is even more interesting - the laws of division are manifested in many respects without any other number except one. That is, it is enough to study the division of a unit into a series of integers, large units, and we will understand how to answer all the questions asked, and at the same time we will meet a very decent number of new stars.

In the meantime, we have not begun a serious study of the subject - a few tricks. Do you know that sharing can be done “vice versa”? Not like we are used to from school, but starting from the end. Let us show this in another example, in which we take the last remainder and, starting from it, we calculate the fraction period. Recall that the remainder in dividing 5 by 3 was equal to 2. What is the last number we subtracted to get a deuce? We do not need to remember, because we know that we always subtract the numbers from the previous remainder multiplied by 10, that is, the last digit of the decrement is always equal to 0. This means that it is enough to sort out the products of the triple by numbers from 1 to 9, = (3,6 , 9,12,15,18,21,24,27), to see - among them, only one ends with 8 and, in total with the remainder 2, gives zero in the last digit of the decrement. So before we get the remainder of 2, we subtracted 18 from 20. Why from 20? Because any other number with zero in the last digit will give the difference X0-18 more than three or less than zero. In the same way, we calculate all the other numbers:

2 - known residue
18 - addition to the number with zero, simultaneously showing the value of the next digit as a result - 6 (6 * 3 = 18)
20 is a suitable number with zero
2 - a number with zero before multiplying by 10 (= 20/10)
18 - addition to the number with zero
20 is a suitable number with zero
...

As a result, we get exactly the same sequence as when dividing by a corner, but "on the other hand." So you can calculate “from the end” the period of any periodic fractions. And what is the pre-period (and the irrelevance of its calculation for this case in the manner shown) we will see further. The whole part of the result is always zero when using the unit as a dividend, so again we are deprived of the need to calculate something else, except for the period.

Now remember how we divide the unit into three: $$$1/3 = 0.3 (3)$. Everything is simple here, the period is short, there is no pre-period, it seems to be nothing remarkable. But let's try to multiply the result of the division again by three: $$$0.3 (3) * 3 = 0.9 (9)$, i.e $$$0.9 (9) /3=0.3 (3)$. And in the beginning it was like this: $$$1/3 = 0.3 (3)$. Do not notice the difference? There was one at the input, and after direct and reverse actions, we get ... How could I call it easier? That is, if we trace the entire chain of nines to infinity, then we will understand that we have a unit, but still it’s somehow not like that, can you find it? Well, not like the original, and that’s it. Mathematicians will say that these are just two forms of notation of the same number, but everyday understanding of the “same” rebels a little against such definitions. In principle, it is difficult to disagree with mathematicians, because many nines after the decimal point differ from unity in something completely ephemeral, infinitely small and tend to zero in the limit. But specifically, can you encompass with your mind this whole set of infinities? An infinite number of nines, an infinitely small difference, tending to zero when moving along a series of nines to infinity. And now compare this with such a record - 1. One sign - and everything is clear to us. And how many signs were there in discussions about the equality of an infinite number of nines to one? That is, there is still a difference? Or does your brain easily ignore such trifles in a set of differences? But if we do not go to the endless mental gaze in the list of nines, then at the place where we stop, there will immediately be a difference that even mathematicians recognize as significant - if you do not see all the other nines, then we are not at all one. Therefore, the question arises - can you see to the depths of all infinity? In general, whatever you want, mathematicians have ordered this phenomenon to be considered the same number. Therefore, having considered this star too (with the frankness - a strange glow), we move on to the next one.

An interesting conclusion follows from the fact of finding an infinite number of nines - if the divisor of unity is a prime greater than 3, then the resulting period is always divided by 9, and of course by 3, and also with its length more than one character - by 11, and when even more characters - 13, 37, 101 and so on. And this is all independent of the unit divisor, if only it would be simple and more than three. You can check it yourself, for example, divide the 1/7 period equal to 142857 by 3, 9, 11, 13, 37.

Well, before the heaps we ask a simple question - is it possible to construct the period yourself? Yes you can. For example, we want to get the period 0123456789, can we find a dividend and a divisor giving something similar? Can! But without the number 8. Then it will be 1/81. And so that the number 8 appears in its rightful place, we will need to add to the number 81 quite a few digits after the decimal point, or without a decimal point, but then many zeros will be present in the period.

Another regularity - for some unit divisors we can not calculate the period at all, but simply shift it cyclically when we multiply the dividend (unit) by any number. For example - 1/7 = 0. (142857), and 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) and so on. If the dividend is greater than 7, then the whole part of the division result will go to the part before the decimal point, and the period will still consist of the same six digits, but again cyclically shifted - 25/7 = 3. (571428), 86/7 = 12. (285714) etc. How do you like that? Any number when divided by 7 gives a set of the same numbers! Any! Absolutely any. And yes, these "any numbers" are an infinite number. And the result always includes 6 of the same numbers. Further, you will understand why the world of numbers is so structured, but for now, we note that when dividing the unit by 7, we implicitly received absolutely all the necessary information to calculate the period from the result of any other numbers being seven, because we now know that it’s enough just to cyclically shift one the only result of division. That is, it is once again confirmed that there is no need to deal with the division of any numbers, except one, by the number chosen for the study. True, it may be necessary to multiply by some numbers and remember intermediate results, but more on that later.

Now for a more general idea, we will show the “battle map”. A map is drawn to divide the unit by the number under study, while division is performed in all number systems with a base less than the number under study. The map does not include the result of division, that is, the period of the fraction under consideration, but instead, the map contains the residuals obtained at each stage of division by the “corner”. This is how it looks:


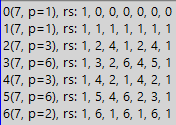
In the above table you see the lines, from 0 to 6. 0 - this is also the basis for the number system. Do you disagree? Let's try to convince. What is a number system? This is the base, multiplied by a certain value, and then added to the result, which at the very beginning is zero. So all numbers are obtained, for example, in the decimal number system. And if the base is zero? Then all terms multiplied by zero will also be equal to zero. But what does that change? Have we violated the rule of constructing numbers in the chosen number system? Therefore, for the generality of the picture on the battle map, we use all the number systems, from 0 to 6 in the case of studying the number 7. But in addition to generality, the line with zeros will have an additional purpose.

But what do all these lines mean? Each row shows us the sequence of residues when dividing the unit by seven in the number system, which is signed in the leftmost column. That is, when dividing 1/7 in a system with a base of 0, we have an initial remainder of 1 (the unit that we divide). Further, as we always did when dividing by a corner, we multiply the first remainder by the base of the number system. We get zero. Now zero is the current remainder. Usually, when calculating the quotient after receiving the remainder equal to zero, and if there are no additional digits in the divisible number, the division is stopped (since the result is obtained). But in our case, we fill out a table that does not tolerate emptiness, and in addition to impatience, it has additional properties that also require the presence of any numbers in all cells. Therefore, we continue to divide and divide the remainder of 0 by 7. Usually, while the remainder is smaller than the divisor, it is multiplied by the base of the number system, but multiplying by zero many times is useless, so we just write that after multiplying by zero the remainder becomes zero again, and Now put it in the table in the next cell. Then repeat the procedure. And so we fill all the cells in the first row with zeros. And then fill in the second line. But it already has another base of the number system - a unit. After dividing 1 by 7, we have the first remainder - one. Then we multiply by the base of the number system, that is, by one. We get again 1. We write in the appropriate cell. Again we multiply by 1, again we get 1, we write again. And so on until the second line is filled. But after these two wonderful lines in every respect, we finally come to a more meaningful division - in the binary system (and the meaning of the first two systems will become clear later). First we have the same unit. Write the unit in the third line. Then we multiply by the base of the number system (by 2). We get 2. 2 less than seven, we can not subtract yet, so we write the remainder 2 in the table. Again, we multiply by 2, we get 4, which again is less than 7, then again it goes to the table without changes. But in the next step we get 8, which is more than 7, so we need to subtract. The result is 1. We write in the table. But earlier we already had a unit, so all the other steps will be the same - so we will add the third line to the end. And in the same way we will add the rest of the lines, but not forgetting that we need to multiply by another basis of the number system.

So, when we finally got the completed table, we can draw some conclusions. First, pay attention to repetitions. For the binary system, we have 1,2,4,1,2,4,1, that is, two times 1,2,4 and then one more time 1. Here, the list 1,2,4 corresponds to the period of the resulting binary fraction. That is, the period will be length 3. And although we used the remainders instead of the numbers from the period, the length did not suffer from this, and therefore all information is saved. And even more - in the table there is really more information leftovers. But more about that later, but for now, we note that all the lines are made of the same length for ease of study and because of the presence of a number of useful properties in this representation. So the lines begin and end with units, which well distinguishes the properties of the number 7. And if we reduced the lines to the length of the period, we would not be able to enjoy the beauty of the symmetrical display of the essence of the number 7.

Now about the information. The balances unambiguously set the number in the corresponding position of the period, therefore the information in this representation is not lost, but since the balances can be greater, for example, the maximum of one decimal position (i.e. 9), the information with their participation becomes the most complete, because one position in the system reckoning cannot tell us that the remainder was, for example, 19, but the remainder 19 will clearly tell you what figure is in the period and from which previous remainder we subtracted the product of the dividend (remember the focus with division “from the end”). And besides, we immediately notice one simple thing - there can be no more residues than $$$N-1$where $$$N$- the investigated number by which we divide the unit. This is a very important point. In addition, it can be easily proved that if during division by a corner the previously encountered residue is repeated, then there will be a repeat of the entire sequence of residues that followed the previously repeated value. So we do not need to take it anymore, once the period is found. If we record only the numbers from the period, then repeating the numbers in the period does not mean the completion of the calculation. Therefore, balances are more important than figures from the period. But the most interesting thing is the remnants of everything $$$N-1$, and therefore the periods are longer $$$N-1$it can not be. So, here we just found the upper limit of the number of digits in the period, moving from the actual digits of the period to the balances. As they say, easy movement of the hand and no fraud. This is the benefit of more complete information. Well, therefore, the width of our “battle map” for 7 matches is 6 + 1 columns, that is, 6 columns for all possible residues and 1 column for detecting symmetry from units, which is by no means mandatory for all numbers, and therefore it is not worth hiding, saving space under one column.

Well, now take a look at the above “map” in terms of its usefulness. You can immediately notice a set of simple patterns. Each line begins with a unit, and it ends with it. The second position of each row indicates the base of the number system, but the middle of each row contains either N-1 or 1. Note that we did not make any efforts to arrange the numbers in the table in this order, except for simply fixing the division results in the table. But despite our ignoring any order (except for the sequence of steps of division), the order itself arose from nowhere and drew us the letter P from units, put on it a cap of zeros (with a visor from one), divided the table by the middle column of units, and its additions to the number 7 (according to the formula 7-1 = 6). In addition, the order itself placed the number systems in the second column. Compare it with the numbers in the very first left column, they are just added intentionally, so that we know exactly where the number system is. Well, we can easily calculate the period of the resulting fractions ourselves, although for convenience it is indicated in the column with values ​​of the form p = X.

In fact, before you is something like a periodic table, but not for chemistry, but for number theory. In exactly the same way as Mendeleev, you can just looking at the table find some regularity, and then, just like after Mendeleev, the presence of this regularity can be justified and prove that it is repeated for all numbers satisfying a certain set of conditions. And this is the most important in such tables. Just looking at and observing patterns, you can discover laws, for example, number theory. Well, for more thoughtful readers, the road to the full cycle opens up - finding a pattern, you need to prove (or disprove) its relevance for all numbers, or for numbers of a certain class.

As was noted, this table contains complete information about the prime number 7. But from this information we can derive hypotheses regarding all primes. And even some of these hypotheses have already been proved to us, so we just have to check the conclusions of others. Evidence was given by such famous people as, for example, Fermat and Euler. Farm gave us this formula $$$a ^ {(p-1)} \ pmod p = 1$(here the mod operation takes the remainder of dividing the value on the left by the value on the right, in programming it is usually indicated by the% symbol), that is, the remainder of dividing $$$a ^ {(p-1)}$on p is always equal to unity for all primes (namely primes, this is important). But the number 7 is also prime. And each residue in each row can be calculated using the following formula: $$$b ^ i \ pmod N = r$. Here b is the base of the number system (from the English base), i is the position number in the line (from the English index), starting from zero for the first position, N is the number under investigation (in this case - 7), r is the remainder (from the English reminder ) formed at the ith step of dividing by a corner and contained in the ith column of the table. Let us compare the Fermat formula and the formula for calculating the remainder specified by index i. They are identical for the last member of all sequences of residues. And in full accordance with the Fermat formula, for each remainder in the position $$$N-1$we have equality to unity. That is, the pattern observed by the naked eye in the form of a column of units was confirmed and proved back in the time of Fermat (although Fermat did not indulge us with evidence, but usually all his statements were true). Euler added to Fermat’s formula the ability to use it not only for primes, but also for composite numbers. True, you need to know all the divisors of a number, but for small numbers this is not a problem. So in the second table (below) we see the sequence of residues for the number 21, which is composite. Euler proved that the remainder of dividing an arbitrary number to the degree equal to the number of numbers smaller and not having common divisors with N is also equal to one. And it is precisely this fact that we observe in the table for the number 21, for which of the 20 lower numbers, 8 have a common factor with 21, and 12 do not. Therefore, we observe in the 12th column (when indexing from scratch) many units. And these units are not at the end of the lines, because some of the numbers that are less than 21 have common divisors with 21.But for prime numbers, not a single smaller number has common divisors with them, so the number of numbers without common divisors in simple is always greater than in composite. And therefore single residues in the table for simple ones are farther than for compound ones. But note - not all values ​​in the 12th column of the table for 21 are equal to one. Is Euler wrong? No, he just did not intend to use his formula to work with numbers that can be reduced, and just in the lines that are multiples of 3 and 7 (divisors of 21) we have a discrepancy with the Euler formula. In general, it turns out that Fermat and Euler gave us suitable formulas useful for understanding the problems of divisibility of numbers, and the tables given in all their glory confirm the results of Euler and Fermat.


Although it is worth noting that neither Fermat nor Euler knew about the above table. And if they knew, then no one was told about her. Although, on the other hand, in their days, alternative decimal notations were somewhat less popular than in our time. Then even not everyone knew about the decimal system, but they counted only on the fingers. And therefore, the deduced Fermat, and then the formula extended by Euler for the connection of the basis and degree, do not give us an explanation of other laws of this table. Therefore, more stars are waiting for us, and then a period of conditional opening of the electron shells of atoms, with the help of which chemists finally explained the magical predictive properties of the periodic table. But let's start with magic.

From stars to magic

Puzzle lovers know the so-called "magic squares". These are tables in which you need to arrange the numbers so that the sums along the verticals, horizontals and two diagonals are the same. Many people puzzled over and over for a long time putting numbers in the Procrustean bed of restrictions on the amounts, and even managed to fill out quite large squares. But today we met with much more powerful magic. Yes, the periodic table for number theory contains many more restrictions, and even a first-grader who can learn to share the “corner” can fill it. Think about it - the smartest people filled the magic squares, but they did not find a common method of filling, or even advanced in size to a miserable hundred columns. And the first-grader will completely cope with even a billion, if only he had enough time available.Here is such a galaxy, stuffed with stars to the eyeballs, waiting for us in numerical squares.

Let's start listing the obvious patterns

Multiplication. Any row of the table can be multiplied by any other. The result will be a series whose number is calculated as the product of the numbers of the multiplied series, divided by the remainder by the number under study. That is, if we multiply row 2 from the table for 7 by row 3, we get row 6. And if we multiply row row 4 by row 6, we get 24 mod 7 = 3, that is, the third row. And the very property of division modulo (that is, with the remainder) makes all number systems, larger than the number under study, unnecessary. So we do not need a number system with base 24, because the values ​​of the residuals in it will be exactly the same as in the system with base 3. In whatever number system we calculate the remainders from 1/7 division, we always get a result that is already is in the table. Interesting? And this is just the beginning.

Symmetry. Each second column contains the upper and lower parts, which are a reflection of each other. And the remaining columns contain values ​​equal to the complement of the N reflected balance. That is, in the second column of the table for the number 7, the number 1 supplements 6 to 7, 2 supplements 5 and 3 supplements 4. As a result, the formula considered above$$ is complemented by the following system:$b^i \pmod N = r$

$$, for odd columns$(N-j)^i \pmod N = r$
$$, for even columns$j^i \pmod N = r$
$$Here N is the number under study (for example 7), b is the base of the number system, i is the column index starting from zero, r is the value of the remainder in the given b and i cell.$j=N-b$



Horizontal symmetry is expressed by the previously mentioned extreme columns of units and the middle column of units and its complement to N. This works exactly for primes, but for components there are deviations. In addition (again only for primes, but sometimes also for constituents), the dividing middle column always either starts with a unit of the repeating period of the residuals, or gives on the right a series of additions to N for the left half of the series. That is, if the unit is in the middle column, then the left part is repeated. If there is an addition to N, then the same left side goes on, but after subtracting from N. Thus, from the whole table (for prime numbers), you can leave only the upper left square with the side$$ (without a zero row), and all other residual values ​​are unambiguously derived based on information from such a square. Although you should not forget that in general the whole table is derived from the knowledge of one single number - the divisor, while the dividend is a constant equal to 1.Now the sum. Basically for simple, but sometimes for compound, the rules shown below are followed. The horizontal sum (without the last column added for clarity) is always a multiple of the number under study. The vertical sum is also always a multiple of the number under investigation. The sums of residuals within the period from one to one (the period may be less than the width of the table) are either multiple or equal to the number under investigation.$(N-1)/2$



Further divisibility. Rows of residuals between units (residual periods) can be of different lengths, but all row lengths for primes always divide the total length of the table by an integer. That is, if at least one row between units does not completely divide the total length of the table, then this is a composite number (compare the tables for 21 and 7).

Length and uniqueness. Each row of even length and shorter than the width of the table consists of two parts - a series of residues to the middle, and after it a series of additions to N for the initial series of residues. Moreover, all values ​​within the period are unique, that is, they are repeated only with the repetition of the period, but within the period they are never repeated.

Multiplication. If each cell of the table is multiplied by an integer, then we obtain either a cyclic shift of residuals in the case of a period length equal to the width of the table, or a new series in cases where the period is shorter than the width of the table. Moreover, in the case of short periods, all values ​​in the new series will be unique, that is, none of them is in the series obtained by dividing the unit by the number under study, as well as in the series obtained by multiplying by other numbers and in the original series, which we multiplied by a constant. In total, the number of unique periods is equal to the width of the table divided by the length of the period (for prime numbers). And for the constituents in all possible periods there are no “forbidden” residues that, when multiplied by rows that are multiples of the divisors of the number under study, give a remainder of zero, but more on that later.

As a result of multiplication of the series, either a cyclic shift of the period or a new period can be obtained. The new period can also be cyclically shifted, multiplying it by other values. The general rule for choosing a shift or a new period is simple - if in the remainder period there is a number by which we multiply, then we will get a cyclic shift, and if there isn’t such a number, we will get a new series. And of course, this directly applies to periodic fractions, more precisely to their periods (it is necessary to distinguish periods from residuals from periods from numbers in the fraction record, although usually the difference is clear from the context). So in the previously shown example of the number 7, we saw that no matter how you multiply the result of dividing by 7, we always get the same set of digits in the period, but cyclically shifted relative to the standard division 1/7. In the case of the number 7, we have a period (in decimal notation) with a length,coinciding with the width of the table, therefore, no other numbers can be obtained in it (there are no more balances in stock), but only cyclic shifts are possible. But there is one more point - we shared in the decimal system, but there is no such line in the table. This means that to find it, we need to divide 10 by 7 and get the remainder - 3. It is the number system with base 3 that completely repeats the behavior of the decimal system with respect to the remainders, therefore it is in the third row that we see the full period, that is, with a length equal to the width of the table. And in order to get the period in decimal terms from the balances, you can take any remainder and start dividing it by the corner, then as a result there will be all the digits of the fraction period. The shift of the period during multiplication is determined by finding the remainder of the division of the factor by N in the series of residuals. The shift will be equal to the index of the remainder found,that is, we always need to cyclically shift the period from right to left by the number of digits equal to the index of the remainder found.

And a few dependencies between the various numbers studied:


Here we see rows for numbers from 2 to 39 in the binary system. Pay attention to the bottom row. Columns of numbers 1,2,4,8,16,32 go up from it. After the number 32, we see a column of values ​​increasing by one (25,26,27, ...). In the next column, the values ​​increase by three. Then on 6, 13, 26, etc. The increase “switches” after reaching a value that is greater than the number under investigation (the column on the left in brackets, before the length of the period). So growth per unit switches to growth by two, then by three, etc. In general, all such columns begin with$$ , where i is the column index.$2^i$ Below $$value does not change, but above changes in accordance with the formula$2^i$$$ , where j is the increment when shifting one row up (greater than zero). That is, while the row number is between$2^i/j$$$$2^i/j$ and $$, the increment is equal to j. After crossing the border$2^i/(j+1)$$$ , the increment becomes equal$2^i/(j+1)$$$ , then the border will be$j+1$$$ , after it the increment will be$2^i/(j+2)$$$$j+2$ etc.Exactly the same regularity is characteristic for any base of number systems, that is, all lines can be replaced by rows of number system 10 (and in the image we see the results for the binary system), or any other, and at the same time the regularity will be preserved, but with the replacement 2 in the formula on another basis of the number system.

The above is not a complete list of patterns, but puzzle lovers probably already have enough to try to fill out a similar square, for example, for prime numbers 11, 13, 17. Try, but do not use the method of division by corner or exponentiation. Suddenly you will discover some other regularity by which such squares are formed!

Predictions

Crystal ball owners tend to predict the future, but we can also predict something from our tables. You have probably already noticed - the last even columns of units are found only in primes. That is, one glance at the table is enough to understand whether a number is a prime number or not. This is the first prediction for our crystal ball. The second prediction is the fraction period in the number system$$ (here k is any integer greater than zero) is always 2. The fraction period in the number system$k*N-1$$$ always equal to 1 and all values ​​in it are also equal to 1. For example, for the studied number N = 11 with k = 1, we have$k*N+1$$$ , i.e. in decimal notation$k*N-1=10$$$ , where the length of the period is 2, as predicted above. Now we predict the complement to the Euler and Fermat formulas. First, recall that each remainder can be calculated by having its position number and the base of the number system using the formula$1/11=0.(09)$

$$, where b is the base of the number system, i is the position starting from zero, N is the number under investigation. This formula corresponds to the formulas of Fermat and Euler, if in it we take the position equal to the values ​​proposed by Fermat and Euler. But besides the pattern$b^i \pmod N$$$ given to us by Fermat, the regularity of the middle column gives us a similar formula -$a^{(p-1)} \pmod p = 1$$$ , that is, any number to the power of a prime, minus one divided by 2, will give us either unity or p-1, where p is a prime. The formula can be extended to the case when the number of periods from one to one within the entire table is odd and the length of the period is even.$a^{(p-1)/2} \pmod p = \{1,p-1\}$ Then $$, where k is any integer, p is a prime. This formula reflects the regularity of repetition of the second part of the period of even length, but with subtraction from the studied number, this dependence was described a little higher. For an even number of periods of even length, one can also express by the formula the dependence of the residues from the right half of the period on the residues from the left half. Now we’ll predict how to find all the divisors of a number from such a table. To do this, look again at the table for the number 21:$a^k \pmod p = p - (a^{(p-1)/2+k} \pmod p)$




It is immediately clear that very few rows end with a unit, this indicates the composite nature of the number. As Euler showed in his formula for comparing the degree of a compound number with the remainder of 1, the exponent in this case cannot be equal to the compound number minus one (that is, the value that determines the extreme right position in the table), so in the case of number 21 we see the majority rows without a unit at the end. Nevertheless, we also see several rows with units. Why is the Euler formula not fulfilled for them? Pay attention to their period, it is equal to 2 or 1. That is, as is typical for many formulas, the Euler formula gives us one solution from the set, and in this set there are guaranteed units at exactly the positions indicated by the formula, that is, before the last place in the table, but since the period is short, then he,repeating many times, sometimes it successfully fits into the total width of the table and we get one at the end of some rows. This situation is typical for a whole set of numbers, which are called pseudo-simple, because they impersonate simple ones, putting units in the right row in some rows. But this does not prevent us from seeing those series in which there is no unit at the end, and therefore this situation does not in any way affect the fundamental possibility of determining the simplicity or composite nature of the number from the proposed table. Although in reality, principles are often found with limitations of our capabilities, but more on that later.putting units on the right in some rows. But this does not prevent us from seeing those series in which there is no unit at the end, and therefore this situation does not in any way affect the fundamental possibility of determining the simplicity or composite nature of the number from the proposed table. Although in reality, principles are often found with limitations of our capabilities, but more on that later.putting units on the right in some rows. But this does not prevent us from seeing those series in which there is no unit at the end, and therefore this situation does not in any way affect the fundamental possibility of determining the simplicity or composite nature of the number from the proposed table. Although in reality, principles are often found with limitations of our capabilities, but more on that later.

Now the divisors of the number 21. Their periods begin and end not with units, but with the divisors themselves. The same applies to all rows in positions that are multiples of divisors. So for divisor 3 we see that in line No. 3 the period begins with a triple and ends with it. The same for row number 7 (despite the fact that the length of the period there is equal to one). And in the same way all multiples of three and seven row numbers behave in the same way. That is, the absence of a unit in periods is a sign of detecting the divisor of the number under study, or a value that is a multiple of the divisor. Well, the unit at the very beginning of such series tells us about the length of the pre-period. For a composite number, the pre-period exists only in number systems that are multiples of the divisors of the number. So if you come across a fraction with a pre-period, you should know that it was obtained after dividing the composite number.The length of the preperiod is equal to the number of residues at the beginning of the series not included in the period of residues. When dividing the unit by the number under study, the pre-period will always consist of zeros. If we multiply the result of dividing by another number (or, equivalently, divide the factor by N), we get all the same period, the rules for the description of which are given above, plus the part of the result of multiplying the factor by the older bits in the pre-period. If the multiplied number is greater than N, then part of the most significant bits will go to the integer part of the result, and the pre-period will remain the same length.the rules for the description of which are given above, plus the part of the result of multiplying the factor by a period that went away by the senior digits in the pre-period. If the multiplied number is greater than N, then part of the most significant bits will go to the integer part of the result, and the pre-period will remain the same length.the rules for the description of which are given above, plus the part of the result of multiplying the factor by a period that went away by the senior digits in the pre-period. If the multiplied number is greater than N, then part of the most significant bits will go to the integer part of the result, and the pre-period will remain the same length.

Note that if we multiply the entire table for a composite number by a multiple of any divisor of the number under study, we get the degeneration of the table when it becomes almost a copy of the table of another number obtained after reducing the researched by its divisor. So below is the table for the number 21 times 3, and below it is the table for the number 7 times 3. If we compare them, it becomes obvious that we have almost a copy of the table for the seven, but three times as wide and height. A full copy will not work, because in the table for 21 numbers that are greater than 7 are valid, and in the table for 7, such numbers are not valid. But if we take this circumstance into account and divide with the remainder the values ​​in the table for 21 by the number 7, then the tables will converge. Although the example of this almost-copy can make sure that outside the subtable for 7, inside the table for 21,there are, as mentioned earlier, complete copies, which it makes sense to simply delete to facilitate perception.



In addition, pay attention to the rows of zeros with lines No. 7 and No. 14. They clearly tell us about the divisibility of the number 21, because we multiplied the result of dividing 1/21 by 3, which is reduced and gives the result 1/7, but row number 7 in this case shows the result of dividing 7/7, where all the remainders are 0. Row number 14 is the result of division 14/7, and there the residues are equal to zero.

We also recall that before the table was multiplied by 3, rows 7 and 14 had values ​​that were multiples of 7, which, if we multiplied by them any values ​​containing a triple divisor, resulted in a multiple of 21. But as we remember, in such a table it is possible to multiply rows, which means that any row containing a remainder that is a multiple of 3, being multiplied by row number 7 or 14, will give zero in the corresponding cell. But the presence of zero in the table means the divisibility of the number by the base of the number system, in the row of which zero is found. Since 21 is divisible only by 3 and 7, there should not be zeros in rows not multiple of 3 and 7. That is why in all rows, except for multiples of 3, we will not find residues that are multiples of 3. That is, if such residues were met, then multiplying a row with such a remainder by row number 7 or 14, we would get a row that does not coincide with the zero row, but containing zeros. Only rowsmultiple of 3 will coincide with the zero row after multiplying by rows 7 or 14. But the zero row in the table is one. How to combine one zero row and zero residues when multiplying by three of rows 7 and 14? It is very simple - you need to prohibit the appearance of multiple 3 numbers in all rows, except multiple 3. But we just came up with this rule, and the laws of the remainder table have always been observed. That is, always, in some kind of entertaining way, nature itself removed (and removes) forbidden numbers from rows not laid for them. Here we have a logical prediction of the algorithm of actions of nature. Or just our logic? It’s worth considering.How to combine one zero row and zero residues when multiplying by three of rows 7 and 14? It is very simple - you need to prohibit the appearance of multiple 3 numbers in all rows, except multiple 3. But we just came up with this rule, and the laws of the remainder table have always been observed. That is, always, in some kind of entertaining way, nature itself removed (and removes) forbidden numbers from rows not laid for them. Here we have a logical prediction of the algorithm of actions of nature. Or just our logic? It’s worth considering.How to combine one zero row and zero residues when multiplying by three of rows 7 and 14? It is very simple - you need to prohibit the appearance of multiple 3 numbers in all rows, except multiple 3. But we just came up with this rule, and the laws of the remainder table have always been observed. That is, always, in some kind of entertaining way, nature itself removed (and removes) forbidden numbers from rows not laid for them. Here we have a logical prediction of the algorithm of actions of nature. Or just our logic? It’s worth considering.Here we have a logical prediction of the algorithm of actions of nature. Or just our logic? It’s worth considering.Here we have a logical prediction of the algorithm of actions of nature. Or just our logic? It’s worth considering.

Why can I use the described tables? For example, they give us the opportunity to generate pseudo-random sequences. And these sequences have a number of useful properties. So in each sequence of residues there are no repetitions. If we need repetitions (for a more complete imitation of randomness), then we have at our disposal values ​​from the fraction period, which can often be repeated. The distribution of residues from the complete set of sequences for primes is always perfectly uniform. The values ​​of a number of residues are automatically kept in the range [1, N-1]. To obtain sequences, we have an infinite number of primes, which makes the number of sequences unlimited. The maximum length of the sequence does not exceed the value of a prime number, which gives a simple way to predict this important parameter.The presence of several sequences, with a period shorter than N, guarantees us that there are no intersections of sequences during their parallel generation, that is, loading all processor cores, we don’t have to think about locks, synchronizations, occurrence checks and the like, which greatly increases the speed of parallel generation. In addition, the generation algorithm (division by corner) is available to elementary school students, and it is also extremely easy to implement programmatically.In addition, the generation algorithm (division by corner) is available to elementary school students, and it is also extremely easy to implement programmatically.In addition, the generation algorithm (division by corner) is available to elementary school students, and it is also extremely easy to implement programmatically.

You can also think about encryption. You can predict the sequence of residuals by knowing the unit divisor, the selected number system and any value from the series encrypting the data (after all, you can encrypt by skipping some residuals). Even when some methods reveal some values ​​from the encryption sequence, the cryptanalyst will still have to guess the chosen number and the base of the number system. If you select two parameters from simple orders of a dozen or two billion (and for them, due to modest size, it is very easy to build a table of their periods, which will allow you to instantly change the cipher at least every second), then using brute force such a cipher can only be cracked by not sorting less than 10 ^ 18 pairs. But even if they crack one data set,then after a certain interval (for example, each message has its own pair), the encryption pair will change and everything must be started again, which may not work out due to the inability to get the value from the encryption sequence for each message (or even part of the message, when changing the key after how many byte). For a regular computer, this is an unresolvable task. Although here everything rests on the discovery of the theory of divisibility sufficient for such purposes (as in the case of widespread asymmetric encryption).Although here everything rests on the discovery of the theory of divisibility sufficient for such purposes (as in the case of widespread asymmetric encryption).Although here everything rests on the discovery of the theory of divisibility sufficient for such purposes (as in the case of widespread asymmetric encryption).

In the next series, we will talk about the theory of divisibility, and about the prizes awaiting interested readers.