Introduction
A few years ago, we decided that it was time to support the SIMD code in .NET . We introduced the System.Numerics namespace with types Vector2 , Vector3 , Vector4 and Vector<T> . These types represent a general-purpose API for creating, accessing, and manipulating vector instructions whenever possible. They also provide software compatibility for those cases where the hardware does not support suitable instructions. This allowed, with minimal refactoring, to vectorize a number of algorithms. Be that as it may, the generality of this approach makes it difficult to apply in order to get the full advantage of all available, on modern hardware, vector instructions. In addition, modern hardware provides a number of specialized, non-vector, instructions that can significantly improve performance. In this article, I'll talk about how we circumvented these limitations in .NET Core 3.0.

Note: There is no established term for Intrisics translation yet . At the end of the article there is a vote for the translation option. If we choose a good option, we will change the article
What are the built-in functions
In .NET Core 3.0, we added new functionality called hardware-specific built-in functions (far WF). This functionality provides access to many specific hardware instructions that cannot be simply represented by more general-purpose mechanisms. They differ from existing SIMD instructions in that they do not have a general purpose (new WFs are not cross-platform and their architecture does not provide software compatibility). Instead, they directly provide platform and hardware-specific functionality for .NET developers. Existing SIMD functions, for example, cross-platform, provide software compatibility, and they are slightly abstracted from the underlying hardware. This abstraction can be expensive, in addition, it can prevent the disclosure of some functionality (when, for example, functionality does not exist, or is difficult to emulate on all target platforms).
New built-in functions , and supported types, are located under the System.Runtime.Intrinsics . For .NET Core 3.0, at the moment, there is one System.Runtime.Intrinsics.X86 . We are working to support built-in functions for other platforms, such as System.Runtime.Intrinsics.Arm .
Under platform-specific namespaces, WFs are grouped into classes that represent groups of logically integrated hardware instructions (often called instruction set architecture (ISA)). Each class provides an IsSupported property IsSupported indicates whether the hardware on which the code is running supports this set of instructions. Further, each such class contains a set of methods mapped to the corresponding set of instructions. Sometimes there is an additional subclass that corresponds to part of the same set of commands, which may be limited (supported) by specific hardware. For example, the Lzcnt class provides access to instructions for counting leading zeros . He has a subclass called X64 , which contains the form of these instructions used only on machines with 64-bit architecture.
Some of these classes are naturally hierarchical in nature. For example, if Lzcnt.X64.IsSupported returns true, then Lzcnt.IsSupported should also return true, since this is an explicit subclass. Or, for example, if Sse2.IsSupported returns true, then Sse.IsSupported should return true, because Sse2 explicitly inherits from Sse . However, it is worth noting that the similarity of class names is not an indicator of their belonging to the same inheritance hierarchy. For example, Bmi2 not inherited from Bmi1 , so the values returned by IsSupported for these two sets of instructions will be different. The fundamental principle in the development of these classes was the explicit presentation of ISA specifications. SSE2 requires support for SSE1, so the classes that represent them are related by inheritance. At the same time, BMI2 does not require support for BMI1, so we did not use inheritance. The following is an example of the above API.
namespace System.Runtime.Intrinsics.X86 { public abstract class Sse { public static bool IsSupported { get; } public static Vector128<float> Add(Vector128<float> left, Vector128<float> right); // Additional APIs public abstract class X64 { public static bool IsSupported { get; } public static long ConvertToInt64(Vector128<float> value); // Additional APIs } } public abstract class Sse2 : Sse { public static new bool IsSupported { get; } public static Vector128<byte> Add(Vector128<byte> left, Vector128<byte> right); // Additional APIs public new abstract class X64 : Sse.X64 { public static bool IsSupported { get; } public static long ConvertToInt64(Vector128<double> value); // Additional APIs } } }
You can see more in the source code at the following links source.dot.net or dotnet / coreclr on GitHub
IsSupported checks IsSupported processed by the JIT compiler as runtime constants (when optimization is enabled), so you do not need cross-compilation to support multiple ISAs, platforms, or architectures. Instead, you just write the code using if expressions, as a result of which unused code branches (i.e. those branches that are not reachable due to the value of the variable in the conditional statement) will be discarded when the native code is generated.
It is important that the verification of the corresponding IsSupported precedes the use of the built-in hardware commands. If there is no such check, then code that uses platform-specific commands running on platforms / architectures where these commands are not supported will throw a PlatformNotSupportedException runtime exception.
What benefits do they provide?
Of course, hardware-specific built-in functions are not for everyone, but they can be used to improve performance in operations loaded with calculations. CoreFX and ML.NET use these methods to speed up operations such as copying in memory, finding the index of an element in an array or string, resizing an image, or working with vectors / matrices / tensors. Manual vectorization of some code that turns out to be a bottleneck can also be simpler than it sounds. Vectorization of the code, in fact, is the execution of several operations at a time, in general, using SIMD instructions (one stream of commands, multiple data stream).
Before you decide to vectorize some code, you need to carry out profiling to make sure that this code is really part of the "hot spot" (and, therefore, your optimization will give a significant performance boost). It is also important to carry out profiling at each stage of vectorization, since vectorization of not all code leads to increased productivity.
Vectorization of a simple algorithm
To illustrate the use of built-in functions, we take the algorithm for summing all elements of an array or range. This kind of code is an ideal candidate for vectorization, because at each iteration, the same trivial operation is performed.
An example implementation of such an algorithm may look as follows:
public int Sum(ReadOnlySpan<int> source) { int result = 0; for (int i = 0; i < source.Length; i++) { result += source[i]; } return result; }
This code is quite simple and straightforward, but at the same time slow enough for large input data, as does only one trivial operation per iteration.
BenchmarkDotNet=v0.11.5, OS=Windows 10.0.18362 AMD Ryzen 7 1800X, 1 CPU, 16 logical and 8 physical cores .NET Core SDK=3.0.100-preview9-013775 [Host] : .NET Core 3.0.0-preview9-19410-10 (CoreCLR 4.700.19.40902, CoreFX 4.700.19.40917), 64bit RyuJIT [AttachedDebugger] DefaultJob : .NET Core 3.0.0-preview9-19410-10 (CoreCLR 4.700.19.40902, CoreFX 4.700.19.40917), 64bit RyuJIT
Increase Productivity Through Deployment Cycles
Modern processors have various options for improving code performance. For single-threaded applications, one such option is to perform several primitive operations in a single processor cycle.
Most modern processors can perform four addition operations in one clock cycle (under optimal conditions), as a result of which, with the correct "layout" of the code, you can sometimes improve performance, even in a single-threaded implementation.
Although JIT can perform loop unrolling on its own, JIT is conservative in making this kind of decision, due to the size of the generated code. Therefore, it may be advantageous to deploy a loop, in code, manually.
You can expand the loop in the code above as follows:
public unsafe int SumUnrolled(ReadOnlySpan<int> source) { int result = 0; int i = 0; int lastBlockIndex = source.Length - (source.Length % 4); // Pin source so we can elide the bounds checks fixed (int* pSource = source) { while (i < lastBlockIndex) { result += pSource[i + 0]; result += pSource[i + 1]; result += pSource[i + 2]; result += pSource[i + 3]; i += 4; } while (i < source.Length) { result += pSource[i]; i += 1; } } return result; }
This code is a bit more complicated, but it makes better use of the hardware features.
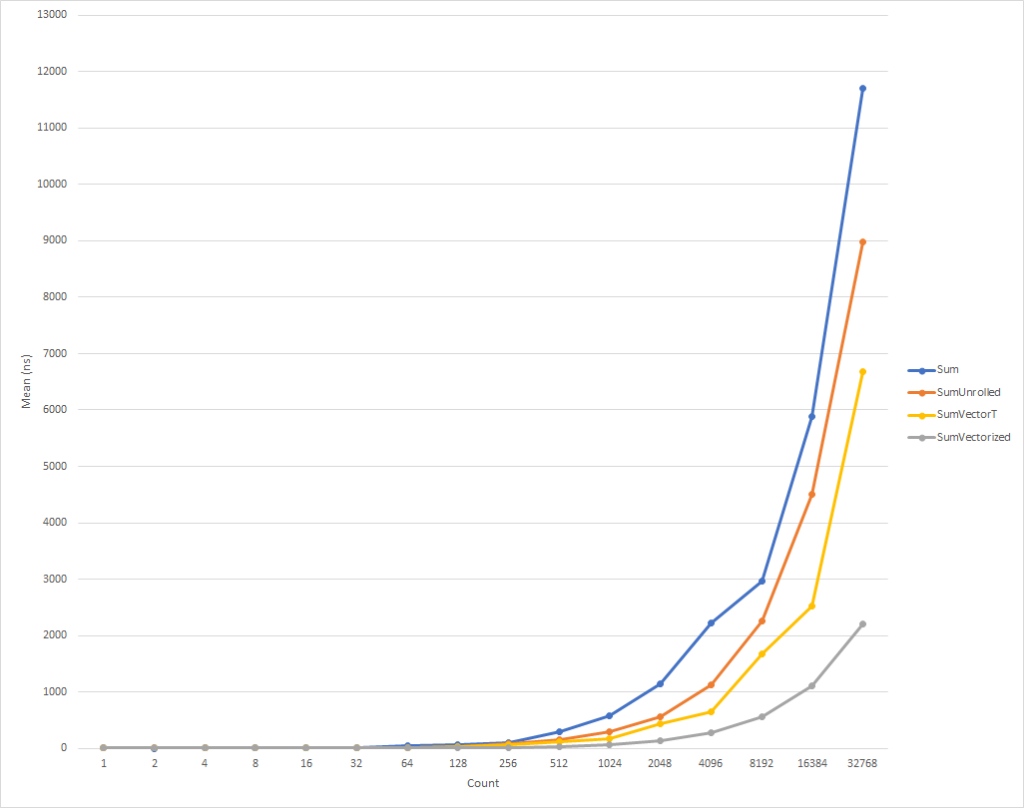
For really small loops, this code runs a little slower. But this trend is already changing for input data of eight elements, after which the execution speed starts to increase (the execution time of the optimized code, for 32 thousand elements, is 26% less than the time of the original version). It is worth noting that such optimization does not always increase productivity. For example, when working with collections with elements of type float "deployed" version of the algorithm has almost the same speed as the original one. Therefore, it is very important to carry out profiling.

Increase productivity through loop vectorization
Be that as it may, but we can still slightly optimize this code. SIMD instructions are another option provided by modern processors to improve performance. Using a single instruction, they allow you to perform several operations in a single clock cycle. This may be better than direct loop unfolding, because, in fact, the same thing is done, but with a smaller amount of generated code.
To clarify, each addition operation, in a deployed cycle, takes 4 bytes. Thus, we need 16 bytes for 4 operations of addition in the expanded form. At the same time, the SIMD addition instruction also performs 4 addition operations, but takes only 4 bytes. This means that we have fewer instructions for the CPU. In addition to this, in the case of the SIMD instruction, the CPU can make assumptions and perform optimization, but this is beyond the scope of this article. What is even better is that modern processors can execute more than one SIMD instruction at a time, i.e., in some cases, you can apply a mixed strategy, at the same time perform a partial cycle scan and vectorization.
In general, you need to start by looking at the Vector<T> general purpose class for your tasks. He, like the new WFs , will embed SIMD instructions, but at the same time, given the versatility of this class, he can reduce the number of “manual” coding.
The code might look like this:
public int SumVectorT(ReadOnlySpan<int> source) { int result = 0; Vector<int> vresult = Vector<int>.Zero; int i = 0; int lastBlockIndex = source.Length - (source.Length % Vector<int>.Count); while (i < lastBlockIndex) { vresult += new Vector<int>(source.Slice(i)); i += Vector<int>.Count; } for (int n = 0; n < Vector<int>.Count; n++) { result += vresult[n]; } while (i < source.Length) { result += source[i]; i += 1; } return result; }
This code works faster, but we are forced to refer to each element separately when calculating the final amount. Also, Vector<T> does not have a precisely defined size, and may vary, depending on the equipment on which the code is running. hardware-specific built-in functions provide additional functionality that can slightly improve this code and make it a little faster (the price will be additional code complexity and maintenance requirements).

NOTE For this article, I forcefully made the Vector<T> size equal to 16 bytes using the internal configuration parameter ( COMPlus_SIMD16ByteOnly=1 ). This tweak normalized the results when comparing SumVectorT with SumVectorizedSse , and allowed us to keep the code simple. In particular, it avoided writing a conditional jump if (Avx2.IsSupported) { } . This code is almost identical to the code for Sse2 , but deals with Vector256<T> (32-byte) and processes even more elements in one iteration of the loop.
Thus, using the new built-in functions , the code can be rewritten as follows:
public int SumVectorized(ReadOnlySpan<int> source) { if (Sse2.IsSupported) { return SumVectorizedSse2(source); } else { return SumVectorT(source); } } public unsafe int SumVectorizedSse2(ReadOnlySpan<int> source) { int result; fixed (int* pSource = source) { Vector128<int> vresult = Vector128<int>.Zero; int i = 0; int lastBlockIndex = source.Length - (source.Length % 4); while (i < lastBlockIndex) { vresult = Sse2.Add(vresult, Sse2.LoadVector128(pSource + i)); i += 4; } if (Ssse3.IsSupported) { vresult = Ssse3.HorizontalAdd(vresult, vresult); vresult = Ssse3.HorizontalAdd(vresult, vresult); } else { vresult = Sse2.Add(vresult, Sse2.Shuffle(vresult, 0x4E)); vresult = Sse2.Add(vresult, Sse2.Shuffle(vresult, 0xB1)); } result = vresult.ToScalar(); while (i < source.Length) { result += pSource[i]; i += 1; } } return result; }
This code, again, is a bit more complicated, but it is significantly faster for everyone except the smallest input sets. For 32 thousand elements, this code executes 75% faster than the expanded cycle, and 81% faster than the source code of the example.
You noticed that we wrote some IsSupported checks. The first one checks if the current hardware supports the required set of built-in functions , if not, then optimization is performed through a combination of sweep and Vector<T> . The latter option will be selected for platforms like ARM / ARM64 that do not support the required instruction set, or if the set has been disabled for the platform. The second IsSupported test, in the SumVectorizedSse2 method, is used for additional optimization if the hardware supports the Ssse3 instruction Ssse3 .
Otherwise, most of the logic is essentially the same as for the expanded loop. Vector128<T> is a 128-bit type containing Vector128<T>.Count elements. In this case, uint , which itself is 32-bit, can have 4 (128/32) elements, this is how we launched the loop.
Conclusion
New built-in functions give you the opportunity to take advantage of the hardware-specific functionality of the machine on which you run the code. There are approximately 1,500 APIs for X86 and X64 distributed over 15 sets, there are too many to describe in one article. By profiling code to identify bottlenecks, you can determine the part of the code that will benefit from vectorization and observe a pretty good performance boost. There are many scenarios where vectorization can be applied and loop unfolding is just the beginning.
Anyone who wants to see more examples can look for the use of built-in functions in the framework (see dotnet and aspnet ), or in other community articles. And although the current WFs are vast, there is still a lot of functionality that needs to be introduced. If you have the functionality you want to introduce, feel free to register an API request via dotnet / corefx on GitHub . The API review process is described here and there is a good example of an API request template specified in step 1.
Special thanks
I want to express special gratitude to the members of our community Fei Peng (@fiigii) and Jacek Blaszczynski (@ 4creators) for their help in implementing the WF , as well as to all members of the community for valuable feedback regarding the development, implementation and ease of use of this functionality.
Afterword to the translation
I like to observe the development of the .NET platform, and, in particular, the C # language. Coming from the world of C ++, and having a little development experience in Delphi and Java, I was very comfortable starting writing programs in C #. In 2006, this programming language (namely the language) seemed to me more concise and practical than Java in the world of managed garbage collection and cross-platform. Therefore, my choice fell on C #, and I did not regret it. The first stage in the evolution of a language was simply its appearance. By 2006, C # absorbed all the best that was at that time in the best languages and platforms: C ++ / Java / Delphi. In 2010, F # went public. It was an experimental platform for studying the functional paradigm with the goal of introducing it into the world of .NET. The result of the experiments was the next stage in the evolution of C # - the expansion of its capabilities in the direction of FP, through the introduction of anonymous functions, lambda expressions, and, ultimately, LINQ. This extension of the language made C # the most advanced, from my point of view, general-purpose language. The next evolutionary step was related to supporting concurrency and asynchrony. Task / Task <T>, the whole concept of TPL, the development of LINQ - PLINQ, and, finally, async / await. , - , .NET C# — . Span<T> Memory<T>, ValueTask/ValueTask<T>, IAsyncDispose, ref readonly struct in, foreach, IO.Streams. GC . , — . , .NET C#, , . ( ) .