Discussions of the pros and cons of the new revolutionary Posit floating-point format are ongoing. The next argument in the discussion was the
statement that in fact the task of Posit is to compactly store data and not be used at all in calculations; at the same time, the calculations themselves are done in Quire arithmetic with greater accuracy, which is also part of the Posit standard.
Well, store so store. What does it mean to “store” numbers after calculations performed with greater accuracy than the storage format allows? It means rounding, and rounding means making errors. Errors can be estimated in different ways - and so as not to be repeated, today we use spectral analysis using the Fourier transform.
Very short introduction
If we take a signal in the form of a sinusoid and perform a Fourier transform on it, then in the spectrum we should get a single peak; in fact, the spectrum may contain both harmonics with a frequency that is a multiple of the fundamental tone obtained as a result of nonlinear distortion, and a noise shelf obtained as a result of noise, interference, and digitization. Here we will measure the level of these noises.
Start
To make it even more interesting, as a test signal we take not one sinusoid, but several; it is necessary to make sure that the periods of these sinusoids fit perfectly into the period of the discrete Fourier transform. In Wolfram Mathematica, this can be done, for example, like this:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
Prime numbers are used here for uneven decimation of frequencies; and j * j shifts the phase of the sinusoid depending on the frequency to avoid strong spikes in the test signal, providing it with a more or less uniform amplitude. The visually received signal looks like this:
Next, we normalize it to unity by the maximum value, then convert it to an integer 32-bit Int, Float, Posit and again to Double. If the authors' claims are correct, then the error introduced by the Double → Posit → Double transformation will be closer to Doublé than to Float.
We will analyze the noise level in standard units for signal processing - decibels, which allow us to compare values on a logarithmic scale. As a tool, I used my own spectrum analyzer, once written for research purposes.
So:
blue - float
red - Posit
purple - Int32
blue - Double
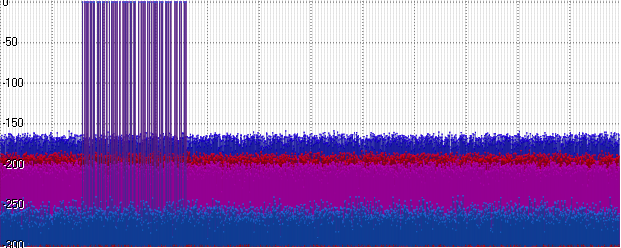
Posit, of course, turned out to be a little better than Float - but he is still far from the Double level. And at the same time - worse than Int32! It is logical - after all, part of the bits it takes an order of magnitude ... Let's use this order - increase the amplitude of our signal to 1000:
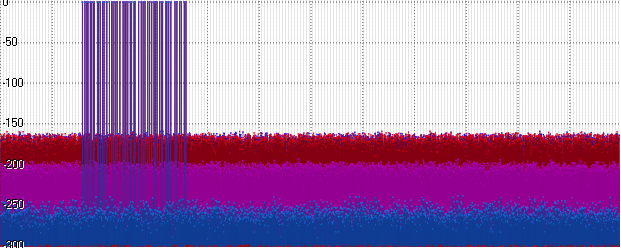
Suddenly (and actually quite expected), the noise at Float and Posit caught up. Go ahead - increase the amplitude to a billion:
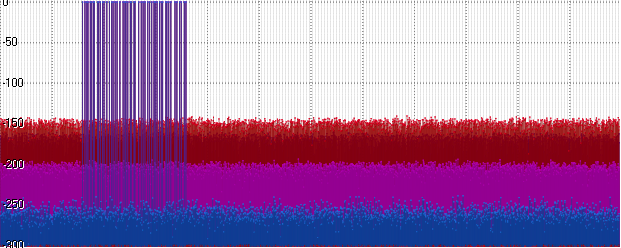
Float shows the same level, and Posit begins to lag. A further increase in amplitude (here 10
15 ) leads to a further increase in the noise shelf:
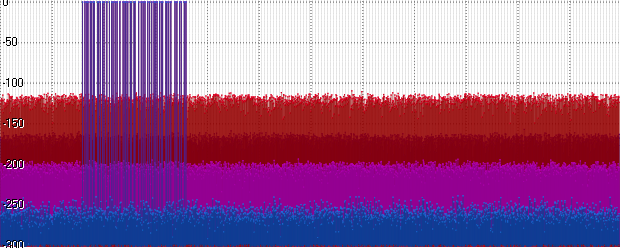
Conclusion
The miracle still did not happen. The spectral analysis did not confirm the authors' statements that using the Posit format as a storage can provide accuracy close to Double. Even under the best conditions, the noise shelf at Posit was only 20 decibels lower than Float, but at the same time, higher than Int32 by 10 decibels, and above Double, by 60 decibels.
Of course, Posit can well find a useful application - as a protection against going beyond the permissible range, when emissions significantly exceeding normal values will not lead to clipping or overflow. But even in this scenario, Posit acts more like a compromise between Int and Float, rather than a clearly better number format.