So our F # journey continues. We looked at some basic types of building blocks, such as records / tuples, now it's time to take a look at the marked up associations.
Labeled unions provide support for values, which can be one of several possible values. Possible values are known as “combined cases”, and take the form shown below:
case-identifier1 [of [ fieldname1 : ] type1 [ * [ fieldname2 : ] type2 …]
Do not worry if this syntax looks intimidating, then what it really comes down to is the presence of a label so that each case can be recognized (distinguished) from the others, and the type for the case of combining. The name has certain rules, such as
- Must start with a capital letter
- It can be an identifier, including the name of the union type itself. This may be a little confusing, but it is useful to describe the case of merging.
Here is an example of a bad id

And here is how something like this might look when using a tag identifier that matches the union register, which, as stated earlier, is perfectly valid
type LabelUnionType = Int of int | String of string
Building tagged associations
So how to build a case of unification? Well, there are different ways, you can use one of the following approaches:
let currentLabelUnionType1 = 13 printfn "let currentLabelUnionType1 = 13" printfn "%O" currentLabelUnionType1 let currentLabelUnionType2 = Int 23 printfn "let currentLabelUnionType2 = Int 23" printfn "%O" currentLabelUnionType2 printfn "%A" currentLabelUnionType2 let currentLabelUnionType3 = "Cat" printfn "let currentLabelUnionType3 = \"Cat\"" printfn "%O" currentLabelUnionType3 printfn "%A" currentLabelUnionType3 let currentLabelUnionType4 = String "Cat" printfn "let currentLabelUnionType4 = String \"Cat\"" printfn "%O" currentLabelUnionType4 printfn "%A" currentLabelUnionType4
Which at startup can give the following results when launched through the printfn function (I use the% A or% O printfn formatter below):

You can pretty much use any type in combining cases like
- Tuple
- documentation
- Other types
The only rule is that the type must be defined before your union case can use it.
Here is an example that uses a tuple type in cases of union:
type unionUsingTuples = CCY of (int * String) | Rates of (int * decimal) ..... ..... let tupledUnion = (12, "GBP")
Empty Unions
You can also use empty unions. Which are those where you do not specify a type. This makes them much more similar to the standard .NET enumeration values. Here is an example:
type Player = Cross | Nought .... .... let emptyUnion = Cross
How about similar cases by type
An eagle eye, like you, can see the problem. What would happen if we had something like this:
type PurchaseOrders = Orders of (string * int) | Empty type ClientOrders = Orders of (string * int) | Empty
This is causing us problems, isn't it. How would we distinguish between these types of demarcated alliances? Fortunately, we can take a fully qualified approach to this, so we can just do it, and everything will work as expected. It should be noted that you can take one more step forward and include the module name if the module is involved (we will learn more about this later in the next article):
let purchaseOrders = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1) let clientOrders = ClientOrders.Orders ("scrubbing brush", 23)
Comparison
As with many F # types, delimited joins are considered equal only if
- The length of their combined case is the same.
- The types of their merging cases match.
- The values of their cases of association are the same
Not equal
Here is an example where equality is not respected:
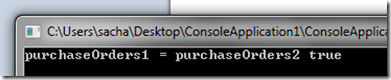
let purchaseOrders1 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1) let purchaseOrders2 = PurchaseOrders.Orders ("10 pack of disks", 1) printfn "purchaseOrders1 = purchaseOrders2 %A" (purchaseOrders1 = purchaseOrders2)

Equal
Here is an example of equality. This is something like regular .NET code, you know, if the members are the same, they have the same values and their correct number, then this is almost the same (if we ignore the hash codes that are):
let purchaseOrders1 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1) let purchaseOrders2 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1) printfn "purchaseOrders1 = purchaseOrders2 %A" (purchaseOrders1 = purchaseOrders2)
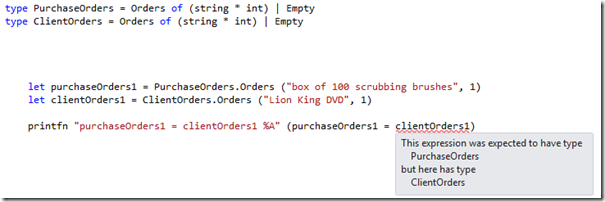
It should be noted that we cannot use equality when we must fully qualify the types of unions, since they are different types, so this will not work:
Comparison Patterns
Below is a small function that takes a Card union and displays the cases of the union it was called with, and simply returns Unit (void, if you remember this from previous articles in this series):
type Card = ValueCard of int | Jack | Queen | King | Ace .... .... let cardFunction card = match card with | ValueCard i -> printfn "its a value card of %A" i | Jack -> printfn "its a Jack" | Queen -> printfn "its a Jack" | King -> printfn "its a Jack" | Ace -> printfn "its a Ace" () //return unit //shows you how to pass it in without a Let binding do cardFunction (Card.ValueCard 8) //or you could use explicit Let binding if you do desire let aceCard = Ace do cardFunction aceCard

So exactly what happens behind the scenes
So now we have seen some examples of how labeled associations work. So, what, in your opinion, could happen if we had a F # library that used markup associations, and we decided to use it from C # / VB.NET. Do you think this will work. Answer: I am sure it will be. I will do a whole post about
Interop somewhere in the future, but I just thought it might be interesting to consider some of this right now for marked-up joins, since they are so different from everything that we see in standard .NET programming.
So, let's take the Card above, which was this code:
type Card = ValueCard of int | Jack | Queen | King | Ace
And run it through a decompiler like Reflector / DotPeek (whatever you have). I used DotPeek and got this C # code for this single F # line. So, as you can see, the F # compiler did a great job to make sure that F # types will work well with regular .NET, such as C # / VB.NET.
using Microsoft.FSharp.Core; using System; using System.Collections; using System.Diagnostics; using System.Runtime.CompilerServices; using System.Runtime.InteropServices; [CompilationMapping(SourceConstructFlags.Module)] public static class Program { [EntryPoint] public static int main(string[] argv) { return 0; } [DebuggerDisplay("{__DebugDisplay(),nq}")] [CompilationMapping(SourceConstructFlags.SumType)] [Serializable] [StructLayout(LayoutKind.Auto, CharSet = CharSet.Auto)] public class Card : IEquatable<Program.Card>, IStructuralEquatable, IComparable<Program.Card>, IComparable, IStructuralComparable { [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public int Tag { [DebuggerNonUserCode] get { return this._tag; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public bool IsValueCard { [DebuggerNonUserCode] get { return this.get_Tag() == 0; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public static Program.Card Jack { [CompilationMapping(SourceConstructFlags.UnionCase, 1)] get { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Jack; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public bool IsJack { [DebuggerNonUserCode] get { return this.get_Tag() == 1; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public static Program.Card Queen { [CompilationMapping(SourceConstructFlags.UnionCase, 2)] get { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Queen; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public bool IsQueen { [DebuggerNonUserCode] get { return this.get_Tag() == 2; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public static Program.Card King { [CompilationMapping(SourceConstructFlags.UnionCase, 3)] get { // ISSUE: reference to a compiler-generated field return Program.Card._unique_King; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public bool IsKing { [DebuggerNonUserCode] get { return this.get_Tag() == 3; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public static Program.Card Ace { [CompilationMapping(SourceConstructFlags.UnionCase, 4)] get { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Ace; } } [CompilerGenerated] [DebuggerNonUserCode] [DebuggerBrowsable(DebuggerBrowsableState.Never)] public bool IsAce { [DebuggerNonUserCode] get { return this.get_Tag() == 4; } } static Card() { } [CompilationMapping(SourceConstructFlags.UnionCase, 0)] public static Program.Card NewValueCard(int item) { return (Program.Card) new Program.Card.ValueCard(item); } [CompilationMapping(SourceConstructFlags.UnionCase, 1)] public static Program.Card get_Jack() { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Jack; } [CompilationMapping(SourceConstructFlags.UnionCase, 2)] public static Program.Card get_Queen() { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Queen; } [CompilationMapping(SourceConstructFlags.UnionCase, 3)] public static Program.Card get_King() { // ISSUE: reference to a compiler-generated field return Program.Card._unique_King; } [CompilationMapping(SourceConstructFlags.UnionCase, 4)] public static Program.Card get_Ace() { // ISSUE: reference to a compiler-generated field return Program.Card._unique_Ace; } public static class Tags { public const int ValueCard = 0; public const int Jack = 1; public const int Queen = 2; public const int King = 3; public const int Ace = 4; } [DebuggerTypeProxy(typeof (Program.Card.ValueCard\u0040DebugTypeProxy))] [DebuggerDisplay("{__DebugDisplay(),nq}")] [Serializable] [SpecialName] public class ValueCard : Program.Card { [CompilationMapping(SourceConstructFlags.Field, 0, 0)] [CompilerGenerated] [DebuggerNonUserCode] public int Item { [DebuggerNonUserCode] get { return this.item; } } } [SpecialName] internal class ValueCard\u0040DebugTypeProxy { [CompilationMapping(SourceConstructFlags.Field, 0, 0)] [CompilerGenerated] [DebuggerNonUserCode] public int Item { [DebuggerNonUserCode] get { return this._obj.item; } } } } }
Recursive cases (tree structures)
Labeled joins can also be used in a recursive manner, where the union itself can be used as one of the types in one or more cases. This makes the marked joins very suitable for modeling tree structures, such as:
- Mathematical expressions
- Abstract syntax trees
- Xml
In fact, MSDN has some good examples.The following code uses a recursive tagged union to create a binary tree data structure. The union consists of two cases: Node, which is a node with an integer value and left and right subtrees, and Tip, which completes the tree.
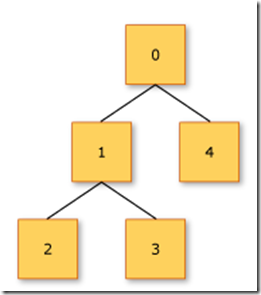
The tree structure for myTree in the example below is shown in the figure below:
And this is how we could model myTree using labeled joins. Notice how we classify the marked-up join as one of the join cases. In this case, the cases of combining either
- Tip (empty union, acts as a standard enumeration in .NET)
- Or a 3-digit tuple from a number, Tree, Tree
It should also be noted that the sumTree function is marked with the keyword rec. What does this magic spell do with our function? Well, this marks sumTree functions as those that will be called recursively. Without the “rec” keyword in the sumTree function, the F # compiler will complain. In this case, the compiler will throw the following error.

But we are good guys, and we will use the right keywords to support our use case, so we continue
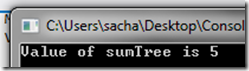
type Tree = | Tip | Node of int * Tree * Tree .... .... .... .... let rec sumTree tree = match tree with | Tip -> 0 | Node(value, left, right) -> value + sumTree(left) + sumTree(right) let myTree = Node(0, Node(1, Node(2, Tip, Tip), Node(3, Tip, Tip)), Node(4, Tip, Tip)) let resultSumTree = sumTree myTree printfn "Value of sumTree is %A" resultSumTree
MSDN also has another good example that I think it would be worth stealing (yes, I’m talking frankly about it now. I think that while you guys / girls are extracting something from this borrowed example that, like I clearly say, I’m borrowed, I’m not at business). Let's look at this example here:
type Expression = | Number of int | Add of Expression * Expression | Multiply of Expression * Expression | Variable of string .... .... .... let rec Evaluate (env:Map<string,int>) exp = match exp with | Number n -> n | Add (x, y) -> Evaluate env x + Evaluate env y | Multiply (x, y) -> Evaluate env x * Evaluate env y | Variable id -> env.[id] let environment = Map.ofList [ "a", 1 ; "b", 2 ; "c", 3 ] // Create an expression tree that represents // the expression: a + 2 * b. let expressionTree1 = Add(Variable "a", Multiply(Number 2, Variable "b")) // Evaluate the expression a + 2 * b, given the // table of values for the variables. let result = Evaluate environment expressionTree1 printfn "Value of sumTree is %A" result