We examined the Monte Carlo method , today we will see how the computer mind plays in 2048 using the good old minimax with alpha-beta clipping.
This article was written with the support of EDISON Software, a company that develops mobile applications and provides software testing services .
Solution spied on by user stackoverflow
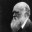ovolve , who noted in the discussion
how to teach AI the game 2048 .
Comment translation from ovolveI am the author of the program mentioned in this thread. You can see the AI
in action or see
the code .
Currently, the program wins in about 90% of cases by executing java-scripts in a browser on my laptop, spending 100 milliseconds to think about the course, working, although not perfectly, but quite well.
Since the game is a discrete state space with complete information, in fact being a turn-based game like chess and checkers, I used the same methods that showed their performance in these games, namely
minimax search with
alpha-beta clipping . Since the links provide a lot of information about this algorithm, I’ll just talk about the two main heuristics that I used in
the static estimation function and formalizing many of the intuitive assumptions made by other people here.
Monotone
This heuristic tries to ensure that all tile values either increase or decrease both left / right and up / down. This heuristic alone reflects the conjecture that many others have mentioned that more valuable tiles should be grouped in a corner. This, as a rule, prevents the accumulation of less valuable tiles and keeps the board organized as smaller tiles cascade into larger ones.
Here is a screenshot of a completely monotonous grid. I got this situation by running an algorithm with the installed eval function in order to ignore other heuristics and take into account only monotony.
Smoothness (smoothness, evenness)
The above heuristic in itself tends to create structures in which neighboring cells are reduced in value, however, of course, neighbors should have the same meaning to unite. Therefore, the heuristic of smoothness simply measures the difference in values between adjacent tiles, trying to minimize their number.
A commentator at Hacker News provided an
interesting formalization of this idea in terms of graph theory.
Translation of formalization with Hacker NewsYesterday I showed this game to a colleague, a lover of graph theory, and we also decided to think about how to solve this game using AI.
The simplest solution is minimax, which, as I see it, is implemented pretty well. If someone here is not familiar with minimax, OP wrote very elegant and well-commented code that would be a great tutorial.
The less computationally intensive approach we proposed was to simulate the game state in the form of a graph G (V, E) , where V is a set of active tiles and E is a set of edges connecting adjacent tiles weighted by function c (v1, v2) , which returns the absolute value of the difference between the two tiles. For each solution, the AI chooses a move that minimizes the sum of the weights of all the edges in the new game state.
The reason for this is that the only way to make progress in the game is to have tiles with the same values next to each other, for which the weight in G will be 0. Thus, the AI should try to minimize the total weight. In the end, there will be a large number on the boards with a large weight of edges to adjacent tiles, so the AI will try to keep these tiles next to other large tiles to minimize the difference.
Since the game is stochastic, the approach I described may not work in the worst case, but it can also be applied to the existing minimax solution as a weight function for each node in the tree.
Here is a screenshot of a perfectly smooth mesh, kindly provided by this excellent
mock fork .
(link to the web archive, while Java scripts on the page work and you can use the keyboard to make a move in any direction - note by the translator).Loose tiles
And finally, there is a penalty for having too few free tiles, since the options can quickly end when the playing field becomes too cramped.
And it's all! Searching the game space while optimizing these criteria gives surprisingly good performance. One of the benefits of using a generic approach like this rather than an explicitly encoded move strategy is that the algorithm can often find interesting and unexpected solutions. If you observe his progress, he often makes amazing but effective movements, such as the sudden change of walls or corners, near which he builds his game.
Small change
The screenshot demonstrates the power of this approach. I canceled the tile limit (so that it continues to grow after reaching 2048), and here is the best result after eight tests.
Yes, this is 4096 along with 2048. =) This means that he reached the elusive 2048 tile on one board.
Java-Script code for minimax with alpha-beta clipping and a static evaluation function from the stackoverflow user ovolve is given below in the article.
The minimax method is devoted to several excellent habr-articles, so we omit the academic detailed explanation of what it consists of. For those who
joined the IT community, I recently heard the beautiful terms “minimax” and “alpha-beta clipping”, but don’t know what this means, let’s try, literally in a couple of paragraphs, to explain the most general meaning.
Minimax
In some games, the process of a game between two players (who make a move in turn) can be represented as a so-called tree of options. In each specific position, each player usually has a choice between different options for his move. And in response to each of these options, an opponent can also be like in many ways.
Option tree fragmentSince at any moment of the game there is complete information about the state of the playing field, the current state of the position can always be accurately estimated. Such a function is called a
static evaluation function or abbreviated
SFO . Moreover, the more important this function is when evaluating a specific position, the more advantageous is the position for one player (let's call it the
maximizing player ). The smaller the numerical value of this function when evaluating a position, the more advantageous is the position for the second player (let's call it the
minimizing player ).
After each move, the position changes, and so its score changes. When considering the tree of options, each player needs to not just prefer those branches in which the rating is most favorable to him. You should also avoid those branches in which the evaluation of the position is favorable for the opponent.
It is assumed that the opponent is also guided by rationalism and also avoids options that could lead him to lose. That is, each player, when choosing an option, proceeds from maximizing his own benefit and at the same time minimizing the opponent’s profit.
This is minimax.
Alpha beta clipping
It is quite obvious: who calculates a tree from a given position to a greater depth, he has more chances to win. But there is one nuisance - the tree of options in games has a nasty habit of branching and growing exponentially with each level of nesting. The counting abilities of programs and even more so people are limited; counting “right up to the mat” is far from always possible. It can easily turn out that the player has counted to a position where he has a good assessment of the playing field, but literally at the next (unreadable) level the opponent has the opportunity to make such a move that radically changes the position estimate to the opposite.
Who is to blame and what to do? The computational complexity is to blame for the complete tree traversal; it is proposed to fight by cutting off unnecessary branches. If the player evaluating the position sees that there is some branch of the options tree:
or less profitable for it than other branches that have already been analyzed,
or more beneficial to the opponent than other branches that have already been analyzed,
then the player discards this branch, does not waste time and resources on considering sub-options from this obviously worse branch for him.
This allows you to allocate more computational resources for calculating more favorable branches for a greater rendering depth in the options tree. In the process of evaluating the playing field at different levels of the options tree, the player operates with two dynamically changing coefficients -
alpha (the value of the SFD that is minimally encountered in the branch - i.e. more favorable for the minimizing player) and
beta (the value of the SFO that is most encountered in the branch - i.e. more favorable for the maximizing player). At each level, comparing the SFD of the current position with
alpha and
beta coefficients allows you to sweep (without calculating them completely) branches that are
less beneficial for the player evaluating the position and / or
more beneficial for his opponent.
This is alpha beta clipping.
Minimalax recursive function with alpha beta clipping
2048 with AI is implemented as an Excel application with VBA macros, this is how the minimax algorithm with alpha beta clipping looks like a despicable visual basic. Ovolve code in java-script function AI(grid) { this.grid = grid; }
Static Evaluation Function
Since at each level in the options tree you have to evaluate the playing field (in order to decide for which of the players, the estimated position is actually more advantageous), you need to decide by what criteria to distinguish a good position from a bad one.
We assume that the maximizing player is the person (or AI) who decides which of the 4 directions (up, left, right, down) to move all the tiles in. A minimizing player is that insidious subroutine that randomly generates 2 or 4 in the most inappropriate places.
SFO is compiled from the perspective of a maximizing player. The higher the SFD rating for the playing field, the better the position for the “maximalist”. The lower - the more pleasant the position on the board for the "minimalist".
In the case of 2048 - what factors are considered favorable for the one who moves the tiles?
Monotone
Firstly, it is desirable that the tiles are arranged in ascending / descending order in some directions. If you don’t do this, then when generating new tiles, the playing field will quickly become clogged with randomly arranged tiles of different sizes, which cannot immediately be connected normally with each other.
In the Siberian Federal District, you need to look in all 4 directions (top-down, left-to-right, right-to-left, bottom-up) and calculate where the tiles are a decreasing or increasing progression. If in progression there are tiles that do not fit into the general series, then this reduces the numerical coefficient of monotony. Then, from the 4 coefficients for all directions, the best one is selected, which is taken into account in the total value of the Siberian Federal District.
Smoothness
Moreover, it would be more preferable if the progression from standing in a row of tiles was not just increasing, but non-decreasing (or instead of decreasing row, it is preferable to non-increasing), that is, it is good when the same tiles are nearby, which allows them to collapse into one, gaining points and increasing free space on the playing field.
Therefore, the Siberian Federal District is looking for identical tiles next to it on the playing field and takes into account the number of such pairs in a special coefficient.
Empty cells
Obviously, the more free space, the more room for maneuver and the less likely to lose quickly.
SFO considers empty cells on the field and the more of these, the position is considered more profitable for the maximizing player.
Maximum tile
Since the main thing in this game is to get a large tile on the field, the more the better - 2048, 4096, 8192 (or whatever you have the strength and patience for), the options where the maximum tile value is more should be considered as the most profitable SFD.
Siberian Federal District for 2048
Implementation of Siberian Federal District as a VBA macro Ovolve code in java-script function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
The Excel application itself
can be downloaded from Google .
The application functionality is described
in a previous article, where AI plays using the Monte Carlo method . Today’s solution has been added to the existing Monte Carlo.
All articles of the AI and 2048 series
- Monte Carlo
- Minimax + alpha beta clipping
- Waiting for maximum
- Neural network