
When we were little, our parents had to answer hundreds of questions: why the sky is blue, why the grass is green, why the boiling water is hot, why you can’t eat only sweets, etc. Curiosity and the desire to understand the world around us accompany us all our lives. Someone grows up and these questions become secondary for him, and someone begins to search for answers in physics, chemistry and other sciences. Today we will consider a study by scientists from the University of Paris, in which they decided to examine in more detail the slippery nature of ice. What interesting discoveries scientists have made, we learn from their report. Go.
Study basis
Ice and snow are slippery because they have a low coefficient of friction. If everything was different, then figure skating, hockey, bobsleigh and other winter sports would not be so exciting, and passers-by would not slip on the frozen sidewalk, showing air pirouettes that any skater would envy.
Slippery ice is based on a layer of water with a thickness of 1 to 100 nm, depending on temperature. This was established thanks to the work of Michael Faraday. However, scientists are still arguing about the nature of this layer, the mechanism of its occurrence and interaction with other objects.
In relatively recent studies, it was found that the main role in sliding on ice is played not by friction due to pressure, but by frictional melting: viscous dissipation generates heat, which raises the temperature in the contact region to the melting temperature, resulting in a water-lubricating film. This statement was built on a theoretical basis and molecular measurements, since in practice it is extremely difficult to study due to the fact that a melt-water film is dynamically and self-consistently generated by sliding, which makes the interface between ice and a water film almost elusive for a detailed study. And because of the low contrast of the interface, it simply makes no sense to use standard methods of interferometry.
As it turned out, being such a simple compound, water made many scientists break their heads, who, as a result of their experimental methods for studying its properties on the ice surface, came to completely different conclusions. For example, one method shows that the thickness of the water film is 5-10 microns, and the other is less than 50 nm. And recent measurements of local temperature have excluded the complete melting of the interfacial water film during sliding, which contradicts the explanation described above (frictional melting).
No matter how simple and transparent ice may seem at first glance, the study of its properties turned out to be complicated and confusing. And the reason for this is the inefficiency of the existing methods of study, therefore, in the study we are considering today, scientists have proposed a completely new approach that allows us to separate the various physical components.
Scientists were able to simultaneously study the friction of a millimeter slider (probe) on ice and the corresponding interfacial mechanical properties of a melt water film at the nanoscale. For this, an improved scanning atomic force microscope was used, which was equipped with a nanometer with a nanometer accuracy.
Preparing for the experiment
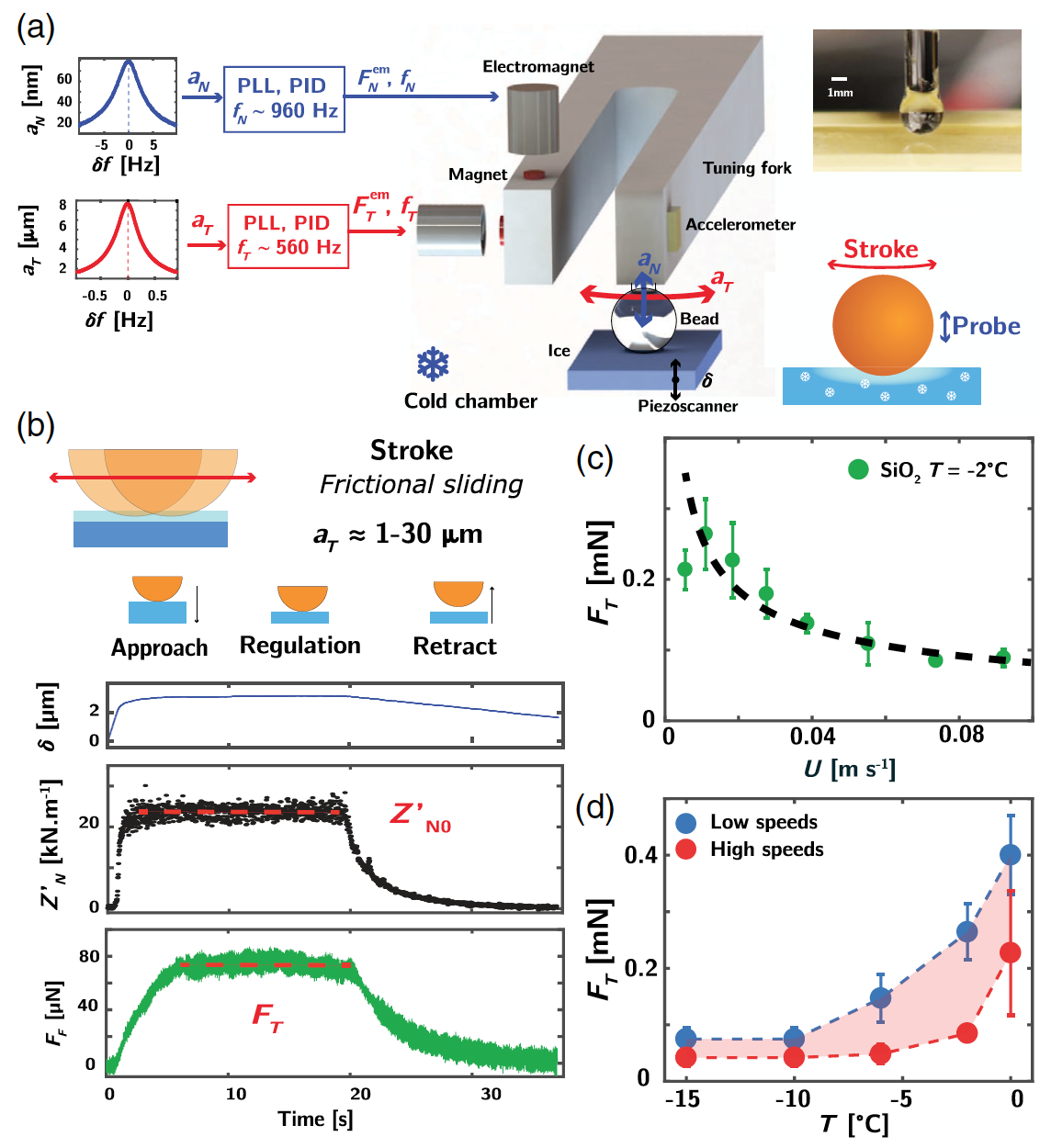 Image No. 1
Image No. 1Figure
1a shows an experimental setup that contains a dual-mode tuning fork for an atomic force microscope. The unit was located in a cold chamber with a controlled temperature of −16 ° C to 0 ° C and a relative humidity of 70–80%. As the studied samples, pieces of ice of a centimeter size obtained from deionized water were used.
A miniature borosilicate glass sphere was glued to one of the teeth of an aluminum tuning fork. The whole system can be very accurately modeled as a load-spring system (harmonic oscillator) of high rigidity K
T ≈ 102 kNm
-1 and Q factor Q
T ≈ 2500. Then, electromagnetic excitation at the tuning fork resonance frequency f
T ≃ 560 Hz leads to lateral oscillatory motion of the sphere parallel to the ice surface (red arrow on
1a ).
The amplitude α
T and the phase shift ϕ
T of the sphere are controlled by an accelerometer glued to one of the teeth. The oscillating sphere is in contact with the ice surface by means of a piezoelectric element with an integrated nanometer resolution position sensor.
Then there is a lateral sliding motion of the sphere, which thereby sharply slides over the ice with an amplitude α
T ~ 1–30 μm and a velocity U = 2πα
T f
T , usually equal to 0.1 ms
−1 .
A phase locked loop maintains the system in resonance by adjusting the excitation frequency f
T , and the tangential friction force F
F is measured by tracking the excitation force F
em T necessary to maintain a constant oscillation amplitude when sliding in accordance with F
F = (K
T / Q
T ) (F
em T / F
em T, - 1) x α
T.Scientists also used normal high-order vibrations (modes) of the tuning fork itself: first, the first mode is excited, associated with the resonant frequency f
N ≃ 960 Hz (K
N ~ 103 kNm
-1 , Q
N ~ 200), and measure the corresponding force.
Using such a small probe (sphere) with a small oscillation amplitude (50 nm) makes it possible to measure the normal mechanical impedance of ice that comes into contact with the probe, Z *
N = F *
N / α
N (F *
N is the complex normal force acting on scope).
The described technique of superposition (separation of one complex into several simple components), according to scientists, allows us to study the mechanical properties of the interface, while tangential sliding along the side surface of ice implements the principles of superposition rheometry (experimental study of deformation and fluidity of a substance). In other words, such a setup allows simultaneous tribometry and rheology of the contact between the sample and the probe (ice and sphere).
Scientists claim that their new method allows for a much more accurate study of the sliding mechanism of objects on ice, and also claim a high degree of accuracy and efficiency of the developed installation, which is confirmed by successful experiments with other liquids (silicone oil, ionic liquids, polyethylene glycol 1000, etc.) .d.). The properties of these fluids were previously established, because when the experimental setup allowed us to obtain results known in advance, this confirmed its operability and effectiveness.
Experiment Procedure
First, a test run of the sphere was carried out, necessary to align the surfaces of the probe and the sample with respect to each other. Then the probe was slowly lowered to the sample to achieve contact between them (
1b ): the indentation depth δ increases, and the friction force increases when the probe begins to slip over the ice. The maximum indentation was kept sufficiently small δ
0 ~ 3 μm to prevent dissipation.
The normal conservative impedance Z '
N was set to Z'
N0 by adjusting the maximum indentation position δ
0 . This adjustment process occurs by fixing the load on the sphere, which is obtained by integrating the Z'N gradient over the indentation depth. And this, in turn, allows you to change the lateral (lateral) friction force for a given load (
1b ).
Following this, the sphere is removed from the sample, due to which the friction force gradually decreases down to zero.
Thus, it is possible to study all aspects of the process of contact of an object with ice at a specified load and at different points of contact.
Experiment Results
Graph
1c represents the lateral friction force F
T as a function of the tangential velocity U associated with α
T in the range 1 ... 30 μm. The friction force does not disappear at low speeds, like friction on a solid. In addition, there is a weak attenuation of the friction force depending on the speed: F
T ∝ U
-γ , where γ ~ 0.3 - 0.5.
It was also found that at a fixed speed, the friction force is proportional to the normal load. This indicates a “hard-like” friction, the coefficient of which is µ = 0.015.
Following the same experiments were carried out, but at different temperatures, which allowed us to determine the temperature dependence of the friction force (
1d ).
At a temperature close to the melting point, the friction force gradually increases. It is worth noting that there is a minimum temperature at which there is a minimum friction force. For this experiment, it was found that this temperature would be below -10 ° C. However, it is not yet possible to investigate lower temperatures (below -16 ° C) on the experimental setup under consideration.
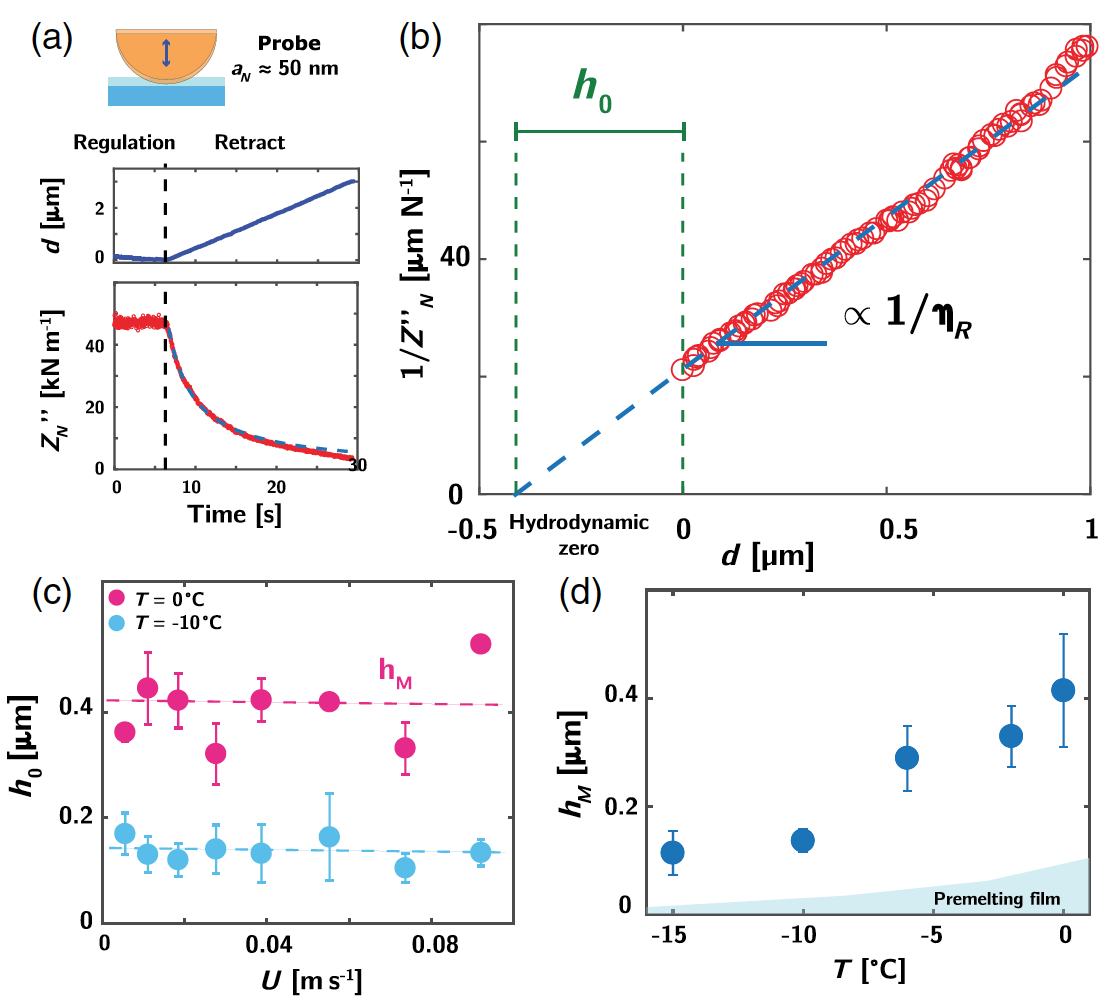 Image No. 2
Image No. 2The next stage of the study was to establish the mechanical properties of the interface during sliding. The real (Z '
N ) and imaginary (Z' '
N ) parts of the mechanical impedance, which are related to the elastic and dissipative response of the interface, were measured.
Figure
2a shows the measurements of normal mechanical impedance at the contact of the probe and the sample, as well as during the removal of the probe from the sample. In this case, a trend similar to the friction force (F
F ) is observed: a plateau during regulation at Z '
N0 , followed by a gradual decrease during probe retraction. The dissipation was estimated by constructing the inverse function of the dependence of the dissipative impedance 1 / Z ''
N on the probe removal distance (
2b ). An important aspect of this measurement is the fact that the impedance varies linearly with respect to the tap distance. Only with a significant retraction distance is this process a little disturbed, and slight deviations from linear behavior occur.
For a non-vanishing sliding velocity U, the intermediate fluid exhibits a viscous reaction during probe removal. The observed linear behavior of 1 / Z '
N as a function of
d also indicates that the viscosity η
R is independent of the indentation depth.
It is also worth noting that the thickness of the hydrodynamic film h
hyd is not fixed, but independently adjusted to achieve a stationary value. In accordance with the linear relationship between h
hyd and 1 / Z '
N , the thickness of the fixed film (h
0 ) can be calculated from measurements of the dissipation modulus Z'
N.It can be seen in
Fig. 2a that, in the control mode, Z ''
N reaches a plateau, expressed as a function of the dependence of time, the speed of contact of the sample with the probe, and normal load. Therefore, using the formula above, the value of the constant film thickness (
2b ) can be derived.
It can also be assumed that the hydrodynamic thickness will be the sum of the actual film thickness and slip length, if any. However, given the hydrophilic nature of ice, it is also to be expected that the slip length will be extremely small (a few nanometers), therefore the hydrodynamic thickness should be regarded as the actual film thickness.
The experiments carried out in which different temperatures, sliding speeds, and loads were applied made it possible to practically determine the constant film thickness.
2c shows how the film thickness varies depending on the tangential velocity. It was previously believed that an increase in speed leads to a direct increase in thickness, but in practice it was found that there is practically no connection. The same weak coupling was observed with respect to thickness and load. But the temperature already had a pronounced effect on the film thickness (
2d ): the thickness increased from 100 to 500 nm with increasing temperature. Also, observations showed that the thickness of the fixed film is approximately 4 times greater than that of equilibrium films in the pre-melting state (light blue color by
2d ).
Another important observation during the experiments was the identification of the viscoelastic rheology of the interfacial film at the time of slip.
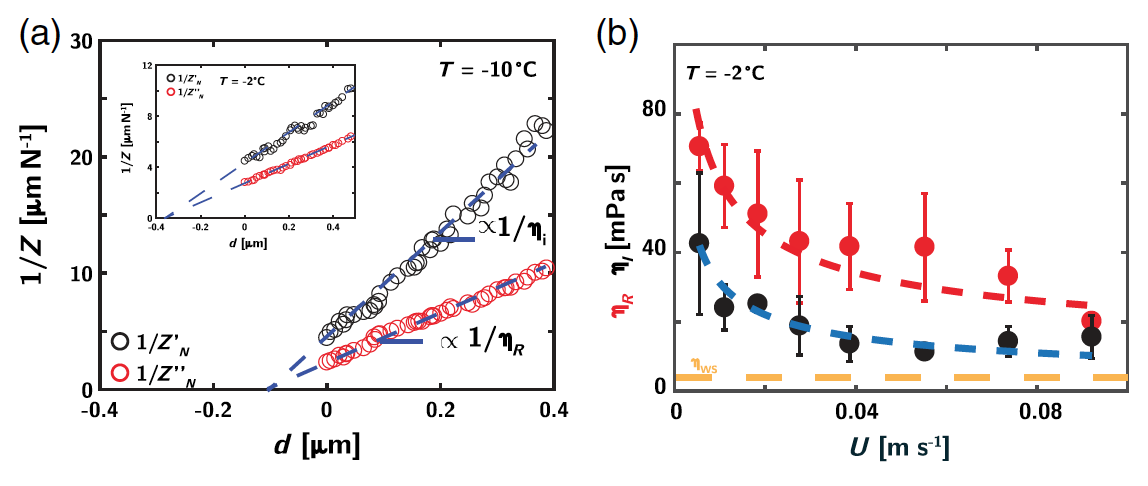 Image No. 3
Image No. 3Graph
3a shows the inversion of the elastic resistance 1 / Z '
N , which shows a linear change with increasing separation distance
d during the removal of the probe from the sample.
The experiments with different variables (speed and temperature) revealed the fact that linear extrapolations of the inverse elasticity and dissipation moduli intersect at the same hydrodynamic zero with an error of 30%. A similar picture is quite common for complex liquids (polymers and polyelectrolytes).
Calculations of the observation results showed that the measured viscosity η
R during sliding is much higher than the typical viscosity of supercooled (below the crystallization temperature) water at the same temperature (orange dotted line at
3b ). The viscosity gradually decays depending on the tangential velocity, similar to the friction force: η
R, I ∝ U
−α , where α ~ 0.3-0.5 (
3b ).
The most interesting thing is that η
R increases very much when approaching the melting point and reaches a value 2 times larger than that of water at 0 ° C (
4a ).
 Image No. 4
Image No. 4All the above observations, according to the researchers themselves, confirm the surprisingly complex rheology of melt water. Firstly, the interfacial water film becomes “as sticky as oil” during sliding (words of scientists), i.e. its viscosity is 2 times higher than that of ordinary water. This observation makes it possible to understand how ice can glide when water is considered to be an extremely poor lubricant. Thus, a thin film on the ice surface limits the indentation of an object sliding on it, which avoids direct contact between these two solids (ice and a blade of skates, for example).
It turns out that the water formed in the form of a film on the surface of the ice at the time of sliding is an excellent lubricant, unlike plain water.
Scientists decided to once again test their model, but with the addition of a hydrophobic coating of the probe, since in winter sports such a coating (for example, wax) is very often used to reduce friction.
The experimental setup differed only in that the spherical glass probe this time was coated with a layer of monosilane (SiH
4 ).
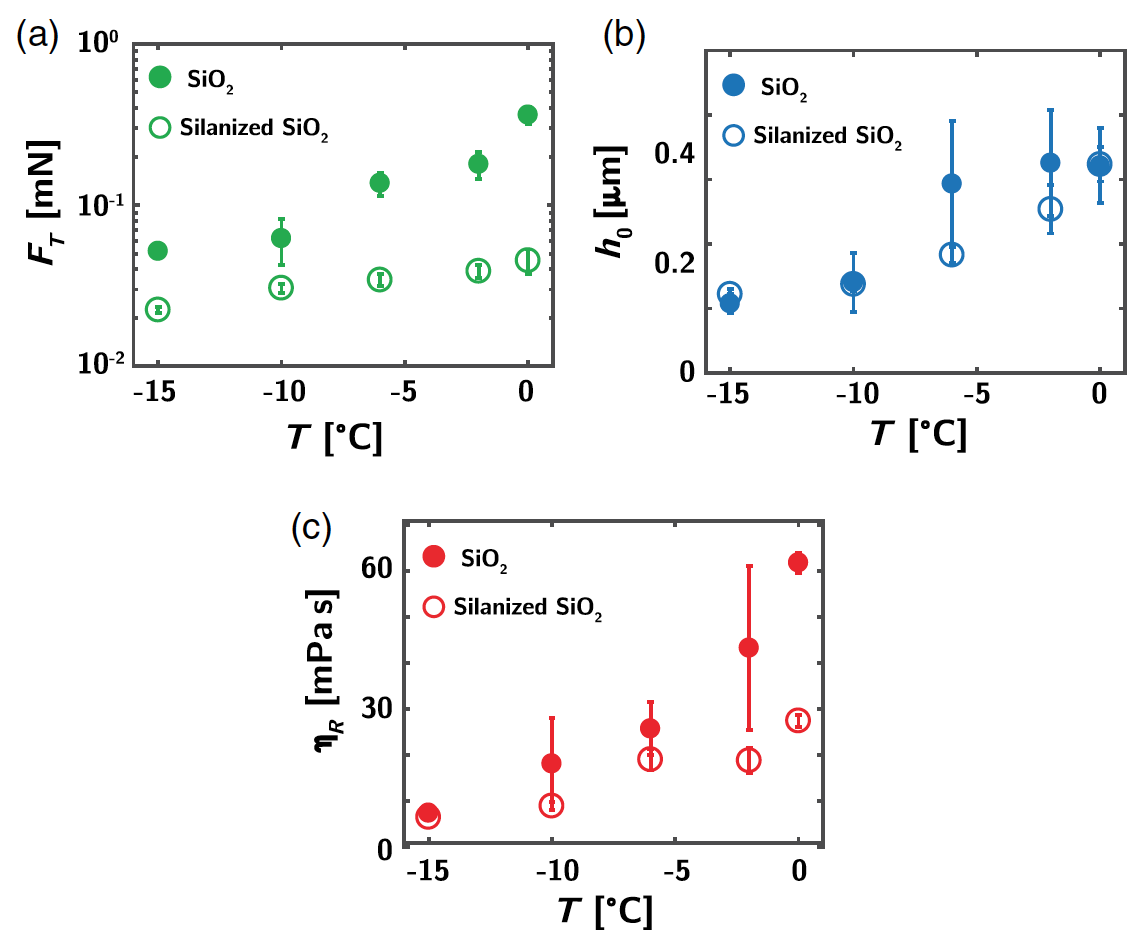 Image No. 5
Image No. 5Indeed, friction in comparison with previous experiments decreased by 10 times. The decrease in friction became more pronounced when the melting point was reached.
It was found that the decrease in friction is not related to the changed hydrodynamic film thickness (
5b ). And there are two conclusions: firstly, this eliminates the effect of finite hydrodynamic sliding on the surface, which is usual for complex liquids; secondly, this confirms that the hydrodynamic thickness is not subject to the sliding effect, even in the case of a clean probe (without SiH
4 coating).
Most likely, there is a decrease in the material part of the viscosity for the hydrophobic probe in comparison with the hydrophilic one. This effect is amplified as the temperature approaches the melting point (
5c ).
The experiments performed very well describe various aspects of the influence of nanometer processes on macroscopic friction of ice. But it is impossible to apply such conclusions to snow, since it is an even more complex material. Therefore, its properties in gliding issues have yet to be studied in the future.
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the
report of scientists and
additional materials to it.
Epilogue
Not everything is as simple as it seems. This study, according to the bold statements of its authors, completely changes our understanding of the mechanisms of sliding on ice and the processes that occur at this moment.
The use of a new research method, which is much more accurate than its predecessors, allowed us to obtain amazing results. The water film covering the surface of the ice, at the moment the probe glided over it, became viscous, like oil, thereby preventing contact of the ice and the probe and allowing the probe to slip over the surface.
Scientists believe that their work is not only of theoretical benefit, giving a wider understanding of the environment, but also practical application. The self-lubricating nature of ice leads to the creation and study of soft and phase-varying solids, which can act as anti-wear films.
Be that as it may, now we know what happens when we skate or fall, slipping on ice sprinkled with snow, throwing the bin in the air to the height of the second floor (personal experience :)).
Thank you for your attention, remain curious, look at your feet and have a good working week, guys! :)
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending it to your friends,
cloud VPS for developers from $ 4.99 , a
30% discount for Habr users on the unique entry-level server analog that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share a server? (options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Dell R730xd 2 times cheaper? Only we have
2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - from $ 99! Read about
How to Build Infrastructure Bldg. class c using Dell R730xd E5-2650 v4 servers costing 9,000 euros for a penny?