The twin prime hypothesis is one of the most important and complex mathematics questions. Two mathematicians solved a parallel version of this problem for small numerical systems.

On September 7, two mathematicians
published a proof of a version of one of the most famous open problems in mathematics. The result opens a new front in the study of the hypothesis of
twin primes that has plagued mathematicians for more than a hundred years and is associated with some of the most profound properties of arithmetic.
“We've been skidding for a long time and we are running out of ideas for this task, so it’s natural for anyone to have new ideas,” said
James Maynard , a mathematician from Oxford.
The twin prime hypothesis applies to pairs of primes that differ by 2. The twins are numbers 5 and 7. And 17 and 19. The hypothesis states that there are an infinite number of such pairs among natural numbers. Over the past decade, mathematicians have made significant progress, but they are still very far from a complete solution to the problem.
The authors of the new evidence,
Will Savin of Columbia University and
Mark Shusterman of the University of Wisconsin in Madison, proved the hypothesis for a smaller, but still noticeable mathematical world. They proved its validity in the case of a finite numerical system in which there are only a few numbers.
Such number systems are called “finite fields”. Despite their small size, they retain many of the mathematical properties inherent in countless integers. Mathematicians are trying to find answers to questions of arithmetic in finite fields, and hope to translate these results to all integers.
“The ultimate dream, albeit a bit naive, is that a good understanding of the properties of a finite field can shed light on the world of integers,” Maynard said.
In addition to proving the hypothesis of twin primes, Savin and Shusterman found an even more surprising result regarding the behavior of primes in small numerical systems. They proved with what frequency the twin primes appear at small intervals - and this result makes it possible to extremely precisely control the phenomenon of twin primes. Mathematicians dream of achieving similar results with ordinary numbers; they explore new evidence in search of ideas applicable to primes on a number line.
A new kind of prime
The most famous prediction of the twin prime hypothesis is the presence of an infinitely large number of pairs of numbers that differ by 2. However, this statement is more general. It says that there is an infinite number of primes that differ by 4 (for example, 3 and 7), or by 14 (293 and 307), or by any number you specify.
Alfons de Polignac
made this assumption in its modern form in 1849. Over the next 160 years, mathematicians did not advance much with him. However, in 2013, the ice broke, or at least seriously cracked. That year,
Zhang Ethan proved the presence of an infinitely large number of pairs of primes, differing by no more than 70 million. Next year, other mathematicians, including Maynard and
Terry Tao , seriously reduced this gap. The current record is the proof of the existence of an infinitely large number of pairs of primes that differ from each other by no more than 246.
However, after that, the progress subsided. Mathematicians understand the need for a completely new idea to fully solve this problem. And finite number systems are a good place to look for this idea.
To build a finite field, you first need to extract a finite subset of numbers from natural numbers. You can, for example, take the first five numbers (or any prime number). And instead of, as usual, representing numbers on a number line, imagine a new number system in the form of a dial.
Arithmetic, as you might have guessed, begins to work in a confined space. What will be 4 + 3 in a finite numerical system consisting of five elements? We start with 4, count three divisions clockwise, and come to 2. Subtraction, multiplication and division work in a similar way.

But only there is a catch. In finite fields, the usual definition of a prime does not make sense. On the final field, any number is divided by any other. For example, 7 is usually not divided by 3. But on a final field of five elements - is divided. That's because on this final field the number 7 is equivalent to the number 12 - they both end at the 2 mark of the dial. Therefore, dividing 7 by 3 will give the same thing as 12 dividing by 3 - and 12 divided by 3 will give 4.
Therefore, the hypothesis of twin primes for finite fields refers to simple polynomials - such mathematical expressions as, for example, x
2 + 1.
Suppose, for example, that your final field contains the numbers 1, 2, and 3. These numbers are the coefficients of the polynomial in this finite field, and the “simple” polynomial is one that cannot be factorized into polynomial factors. Therefore, x
2 + x + 2 will be simple, since it cannot be factorized, but x
2 - 1 will not: this is the product of (x + 1) and (x - 1).
Having defined simple polynomials, it is natural to ask a question about simple twin polynomials - pairs of polynomials that are simple and differ by a fixed value. For example, the polynomial x
2 + x + 2 is simple, like x
2 + 2x + 2. They differ by x.
The hypothesis of simple twin polynomials for finite fields indicates the existence of an infinitely large number of pairs of simple twin polynomials that differ not just by x, but by any value.
Neat cuts
The concepts of finite fields and simple polynomials may seem far-fetched, and useless for studying the properties of numbers. But they look like a hurricane simulator - a universe in itself that gives ideas about events taking place in a big world.
“There is an ancient analogy between integers and polynomials, which allows you to convert potentially extremely complex problems related to integers into tasks related to polynomials, which are also potentially complex, but may be easier to solve,” said Shusterman.
Finite fields became famous in 1940 when
Andre Weil developed the exact way to translate the arithmetic of small number systems into the arithmetic of integers. Weil used this connection with amazing results. He
proved , perhaps, the most important problem in mathematics - the Riemann hypothesis - for the case with a set of curves over finite fields (this problem is known by the name of the Riemann geometric hypothesis). This proof, along with a set of additional
Weyl hypotheses, made finite fields a rich landscape for mathematical discoveries.
Weil's key idea was that in finite fields, geometric techniques could be used to find answers to questions about numbers. “This is a feature of finite fields. Many of the tasks you want to solve can be rephrased geometrically, ”said Shusterman.
To understand how geometry appears in such an environment, imagine each polynomial as a point in space. The coefficients of a polynomial serve as coordinates determining its location. Returning to our final field of 1, 2, and 3, the polynomial 2x + 3 is located at the point (2, 3) of the two-dimensional space.
But even in the simplest finite space there is an infinite number of polynomials. You can create more complex polynomials by increasing the exponent of the largest exponent, or the degree of expression. In our case, the polynomial x
2 - 3x - 1 will be represented by a point in three-dimensional space. And the polynomial 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 will be represented by a point in eight-dimensional space.
In the new work, this geometric space represents all polynomials of a given degree for a given finite field. The question turns into the following: is there a way to isolate all points denoting simple polynomials?
The strategy of Savin and Shusterman is to divide the space into two parts. In one part there will be all points corresponding to polynomials with an even number of factors. In the other, all points corresponding to polynomials with an odd number of factors.
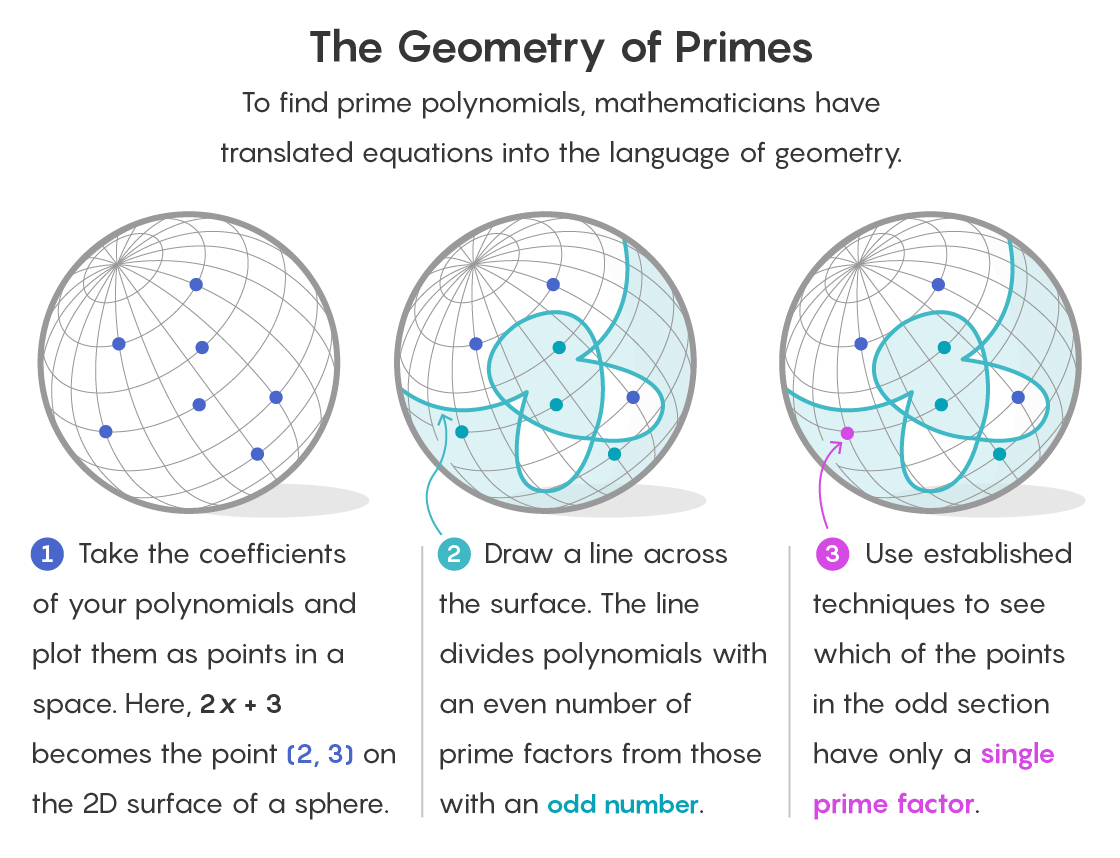
This already simplifies the task. The hypothesis of simple twin polynomials for finite fields applies only to polynomials with one factor (just like a prime has one factor, it is itself). And since the number 1 is odd, part of the space containing polynomials with an even number of factors can be immediately discarded.
The trick is to use division. In the case of a two-dimensional object, for example, the surface of a sphere, it is cut in half by a one-dimensional curve - just as the equator cuts the surface of the Earth. An object with a large number of dimensions can always be cut with an object with the number of dimensions less by one.
But these forms with fewer dimensions, dividing the space of polynomials, are not at all as elegant as the equator. They are drawn according to a mathematical formula called
the Mobius function . At the input, it takes a polynomial, and at the output it gives 1 if the polynomial has an even number of prime factors, -1 if it has an odd number, and 0 if it is factorized (since 16 can be decomposed into 2 × 2 × 2 × 2).
The curves drawn by the Mobius function bend and twist like mad, intersecting with themselves in many places. These places, called singularities, are especially difficult to analyze (they correspond to polynomials that can be decomposed into several identical prime factors).
The fundamental innovation of Savin and Shusterman was that they found the exact way to cut loops with fewer measurements into shorter segments. These segments were easier to learn than the whole loop.
Having compiled a catalog of polynomials with an odd number of prime factors — and this was the most difficult — Savin and Shusterman were faced with the task of determining which of them are simple and which are twins. To do this, they applied several formulas used by mathematicians to study prime numbers among ordinary ones.
Savin and Shusterman used their technique to prove two important points regarding simple polynomials in certain finite fields.
First, the hypothesis of twin primes in finite fields is true: there are infinitely many pairs of twin polynomials that differ by any given value.
Secondly, and more importantly, this work provides an accurate calculation of the number of simple twin polynomials that can be found among polynomials of a certain order. This is analogous to knowing how many twin primes are inside any sufficiently long interval on a number line - and this is just the dream of mathematicians.
“This is the first work that gives a quantitative analogy of what should be true for integers, and this is a really outstanding result,” said Ziv Rudnik of Tel Aviv University. “So far, nothing like this has happened.”
The proof of Savin and Schusterman shows how, almost 80 years after Andre Weil proved the Riemann hypothesis for curves over finite fields, mathematicians are still stubbornly moving in this direction. Now, mathematicians who deal with the twin prime hypothesis will turn to the work of Savin and Shusterman, and perhaps it will give them a deep source of inspiration.