A recent study,
“Using and attributing Stack Overflow code snippets in GitHub projects,” suddenly found that most of the time in open source projects, my
answer was written almost ten years ago. Ironically, there’s a bug.
A long time ago…
Back in 2010, I was sitting in my office and doing nonsense: I was
fond of code golfing and
added a rating to Stack Overflow.
The following question attracted my attention: how to display the number of bytes in a readable format? That is, how to convert something like 123456789 bytes to “123.5 MB”.
 Good old 2010 interface, thanks The Wayback Machine
Good old 2010 interface, thanks The Wayback MachineImplicitly, the result would be a number between 1 and 999.9 with the appropriate unit.
There was already one answer with a loop. The idea is simple: check all degrees from the largest unit (EB = 10
18 bytes) to the smallest (B = 1 byte) and apply the first, which is less than the number of bytes. In pseudo code, it looks something like this:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Usually, with the correct answer with a positive rating, it is difficult to catch up with it. In the Stack Overflow jargon, this is called the
problem of the fastest shooter in the West . But here the answer had several flaws, so I still hoped to surpass it. At the very least, code with a loop can be significantly reduced.
Well this is algebra, everything is simple!
Then it dawned on me. The prefixes are kilo-, mega-, giga-, ... - nothing more than the degree of 1000 (or 1024 in the IEC standard), so the correct prefix can be determined using the logarithm, and not the cycle.
Based on this idea, I published the following:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
Of course, this is not very readable, and log / pow is inferior in efficiency to other options. But there is no loop and almost no branching, so the result is pretty beautiful, in my opinion.
Mathematics is simple . The number of bytes is expressed as byteCount = 1000 s , where s represents the degree (in binary notation, the base is 1024.) Solution s gives s = log 1000 (byteCount).
The API does not have a simple expression log 1000 , but we can express it in terms of the natural logarithm as follows s = log (byteCount) / log (1000). Then we convert s to int, so if, for example, we have more than one megabyte (but not a full gigabyte), then MB will be used as the unit of measurement.
It turns out that if s = 1, then the dimension is kilobytes, if s = 2 - megabytes and so on. Divide byteCount by 1000 s and slap the corresponding letter into the prefix.
All that remained was to wait and see how the community perceived the answer. I could not have thought that this piece of code would be the most replicated in the history of Stack Overflow.
Attribution Study
Fast forward to 2018. Graduate student Sebastian Baltes publishes an article in the scientific journal
Empirical Software Engineering entitled
“Using and attributing Stack Overflow code snippets in GitHub projects .
” The topic of his research is how much the Stack Overflow CC BY-SA 3.0 license is respected, that is, do authors point to Stack Overflow as a source of code.
For analysis, snippets of code were extracted from the
Stack Overflow dump and mapped to the code in the public GitHub repositories. Quote from the abstract:
We present the results of a large-scale empirical study analyzing the use and attribution of non-trivial fragments of Java code from SO answers in public GitHub (GH) projects.
(Spoiler: no, most programmers do not comply with the license requirements).
The article has such a table:
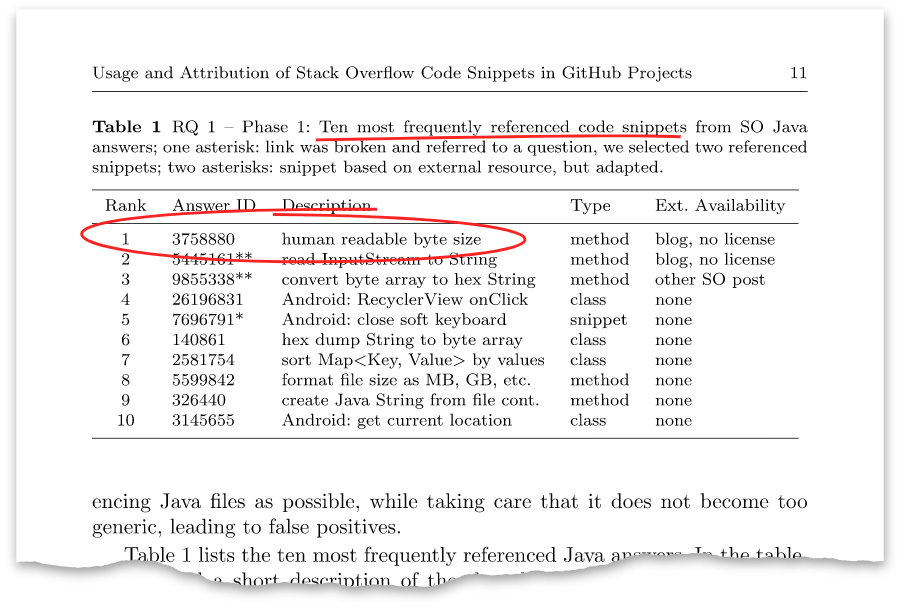
This answer above with the identifier
3758880 turned out to be the very answer that I posted eight years ago. At the moment, he has more than one hundred thousand views and more than a thousand pluses.
A quick search on GitHub really produces thousands of repositories with the code
humanReadableByteCount .
Search for this fragment in your repository:
$ git grep humanReadableByteCount
A funny story as I found out about this study.
Sebastian found a match in the OpenJDK repository without any attribution, and the OpenJDK license is not compatible with CC BY-SA 3.0. On the jdk9-dev mailing list, he asked: is the Stack Overflow code copied from OpenJDK or vice versa?
The funny thing is that I just worked in Oracle, in the OpenJDK project, so my former colleague and friend wrote the following:
Hi,
Why not ask the author of this post directly on SO (aioobe)? He is a member of OpenJDK and worked at Oracle when this code appeared in the OpenJDK source repositories.
Oracle takes these issues very seriously. I know that some managers were relieved when they read this answer and found the “culprit”.
Then Sebastian wrote to me to clarify the situation, which I did: this code was added before I joined Oracle and I have nothing to do with the commit. It's better not to joke with Oracle. A few days after the ticket was opened, this code was deleted .
Bug
I bet you already thought about that. What kind of error in the code?
Again:
public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }
What options?
After exabytes (10
18 ) are zettabytes (10
21 ). Maybe a really large number will go beyond kMGTPE? Not. The maximum value is 2
63 -1 ≈ 9.2 × 10
18 , so no value will ever go beyond exabytes.
Maybe the confusion between SI units and the binary system? Not. There was confusion in the first version of the answer, but it was fixed quite quickly.
Maybe exp ends up zeroing, causing charAt (exp-1) to crash? Also no. The first if statement covers this case. The exp value will always be at least 1.
Maybe some strange rounding error in the extradition? Well, finally ...
Many nines
The solution works until it approaches 1 MB. When
"1000,0 kB" bytes are specified as input, the result (in SI mode) is
"1000,0 kB" . Although 999,999 is closer to 1000 × 1000
1 than to 999.9 × 1000
1 , the signifier 1000 is prohibited by the specification. The correct result is
"1.0 MB" .
In my defense, I can say that at the time of writing, such an error was in all 22 published answers, including Apache Commons and Android libraries.
How to fix it? First of all, we note that the exponent (exp) should change from 'k' to 'M' as soon as the number of bytes is closer to 1 × 1,000
2 (1 MB) than to 999.9 × 1000
1 (999.9 k ) This happens at 999,950. Likewise, we should switch from 'M' to 'G' when we go through 999,950,000 and so on.
We compute this threshold and increase
exp if
bytes greater:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;
With this change, the code works well until the number of bytes approaches 1 EB.
More Nines
When calculating 999 949 999 999 999 999, the code gives
1000.0 PB , and the correct result is
999.9 PB . Mathematically, the code is accurate, so what happens here?
Now we are faced with
double constraints.
Introduction to floating point arithmetic
According to the IEEE 754 specification, floating point values close to zero have a very dense representation, while large values have a very sparse representation. In fact, half of all values are between -1 and 1, and when it comes to large numbers, a value of size Long.MAX_VALUE does not mean anything. Literally.
double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
See "Floating Point Bits" for details.
The problem is represented by two calculations:
- Division in
String.format and
- Expansion threshold
exp
We can switch to
BigDecimal , but it's boring. In addition, problems arise here, too, because the standard API does not have a logarithm for
BigDecimal .
Decrease Intermediate Values
To solve the first problem, we can reduce the value of
bytes to the desired range, where accuracy is better, and adjust
exp accordingly. In any case, the final result is rounded, so it does not matter that we throw out the least significant categories.
if (exp > 4) { bytes /= unit; exp--; }
Least significant bits setting
To solve the second problem
, the least significant bits
are important to us (99994999 ... 9 and 99995000 ... 0 must have different degrees), so we have to find a different solution.
First, note that there are 12 different threshold values (6 for each mode), and only one of them leads to an error. An incorrect result can be uniquely identified because it ends in D00
16 . So you can fix it directly.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;
Since we rely on certain bit patterns in floating point results, we use the strictfp modifier to ensure that the code works independently of the hardware.
Negative input values
It is unclear under what circumstances a negative number of bytes may make sense, but since Java does not have an unsigned
long , it is best to handle this option. Right now, input like
-10000 B produces
-10000 BLet's write
absBytes :
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
The expression is so verbose because
-Long.MIN_VALUE == Long.MIN_VALUE . Now we do all the
exp calculations using
absBytes instead of
bytes .
Final version
Here is the final version of the code, shortened and condensed in the spirit of the original version:
Note that this began as an attempt to avoid loops and excessive branching. But after smoothing out all border situations, the code became even less readable than the original version. Personally, I would not copy this fragment in production.
For an updated version of production quality, see a separate article:
“Formatting byte size in a readable format .
”Key Findings
- There may be errors in answers to Stack Overflow, even if they have thousands of pluses.
- Check all boundary cases, especially in code with Stack Overflow.
- Floating point arithmetic is complicated.
- Be sure to include the correct attribution when copying code. Someone may take you to clean water.